Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Таблица интегралов.

Функция F(x) называется первообразной функцией для функции f(x) на промежутке Х, если в каждой точке х этого промежутка .

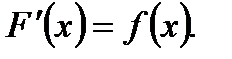Свойство первообразной.

Если F₁(x) и F₂(x) – первообразные для функции f(x) в некотором промежутке Х, то найдется такое число С, что справедливо равенство: .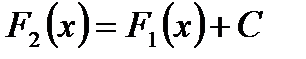

Совокупность всех первообразных для функции f(x) на промежутке Х называется неопределенным интегралом от функции f(x) и обозначается .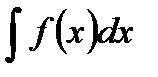

Согласно определению, .

Свойства неопределенного интеграла.

1. Производная от неопределенного интеграла равна подынтегральной функции: .
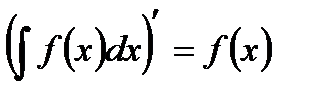2. Дифференциал неопределенного интеграла равен подынтегральному выражению: .
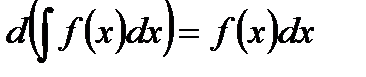3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого: .
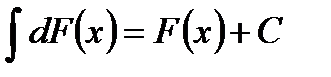4. Постоянный множитель можно выносить за знак интеграла: .
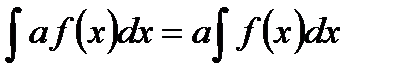5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций:
6. .

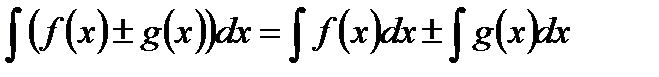Таблица интегралов:

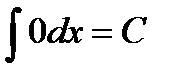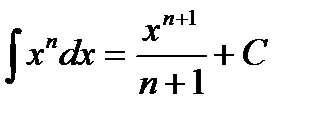;  (при п ¹ –1); ;

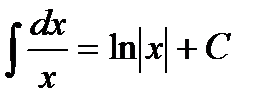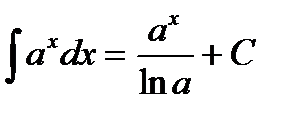 (при а > 0, a ¹ 0);

; ; ;

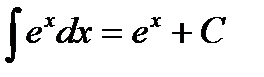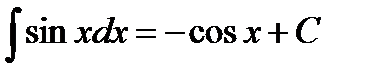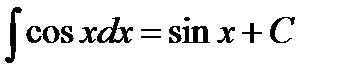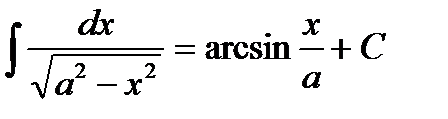 (при );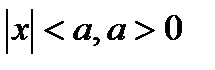

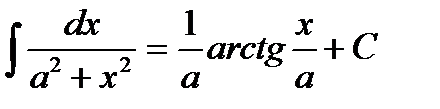 (при a ¹ 0);

;

;

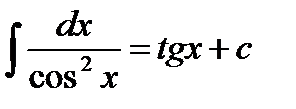
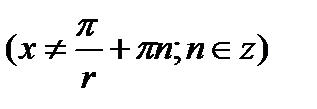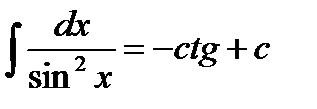
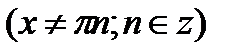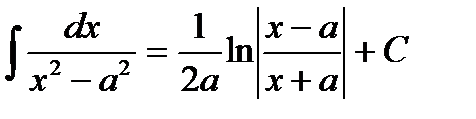 (при a ¹ 0); .

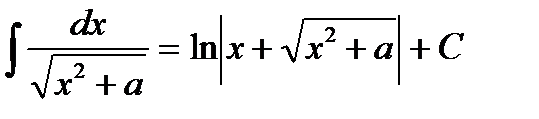Определенный интеграл

Пусть предел интегральной суммы при стремлении 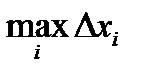 к нулю существует, конечен и не зависит от способа выбора точек х₁, х₂,… и точек x₁, x₂,… Тогда этот предел называется определенным интегралом от функции у=f(x) на [a; b], обозначается 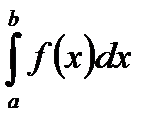, а сама функция у = f(x) называется интегрируемой на [a; b], т.е.

.

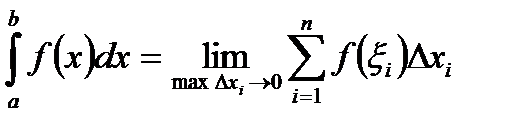Свойства определенного интеграла:

1. Постоянный множитель можно выносить за знак интеграла:

.

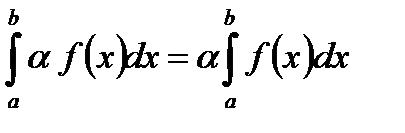2. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций: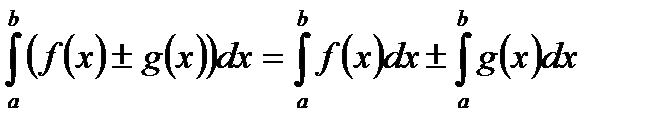

3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е.

.

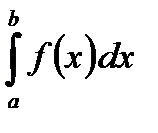
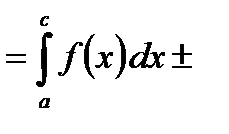
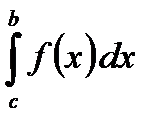4. Если на отрезке [a; b] f(x) £ g(x), то и  £ .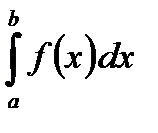

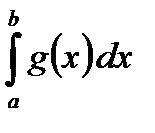5. Если функция у = f(x) непрерывна на отрезке [a; b], то найдется такое значение x Î [a; b], что .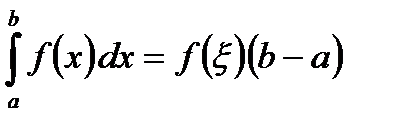

 

Формула Ньютона-Лейбница.

Пусть функция у = f(x) непрерывна на отрезке [a; b] и F(x) первообразная функцией для функции f(x) на отрезке [a; b]. Тогда определенный интеграл от функции f(x) на [a; b] равен приращению первообразной на этом отрезке, т.е. .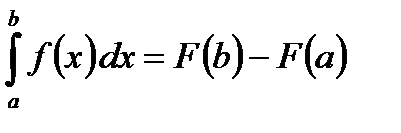

 

Ряды.

Основные понятия

 Числовым рядом называется сумма вида

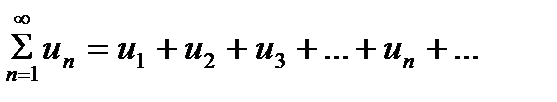
Где числа u₁, u₂, u₃, …. , u_n, … называемые членами ряда, образуют бесконечную последовательность; член u_n называют общим членом ряда.

Суммы:

. . . . . . . . . . .

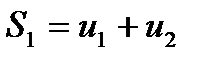
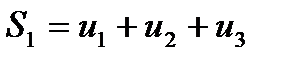
составленные из первых членов ряда, называются частичными суммами этого ряда.

Каждому ряду можно сопоставить последовательность частичных сумм S₁, S₂, S₃,…., S_n Если при бесконечном возрастании номера n частичная сумма ряда S_n стремится к пределу S, то ряд называется сходящимся, а число S – суммой сходящегося ряда, т.е.

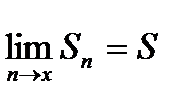 или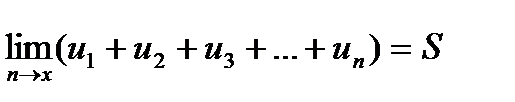

Эта запись равносильна записи

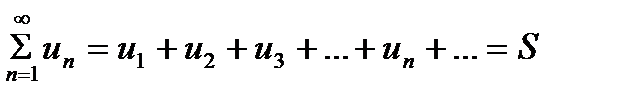
Если частичная сумма S_n ряда при неограниченном возрастании n не имеет конечного предела ( в частности, стремится к +х или к – бесконечность), то такой ряд называют расходящимся.

Если ряд сходится, то значение S_n при достаточно большом n является приближенным выражением суммы ряда S.

Разность r_n = S - S_n называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т.е. 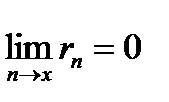, и наоборот, если остаток стремится к нулю, то ряд сходится.