Общая схема исследования функции и построения ее графика.

1. Найти область определения функции.

2. Исследовать функцию на четность – нечетность.

3. Исследовать вид разрыва в точках разрыва (если они есть).

4. Найти вертикальные асимптоты. (Для этого определяются значения левосторонних и правосторонних пределов в точках разрыва и выясняется, конечные они или бесконечные. Если пределы бесконечны, то прямая х = х₀ – вертикальная асимптота).

5. Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты (для этого определяются пределы функции на бесконечности. Если 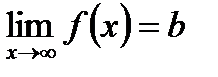, то у = b – горизонтальная асимптота. Если 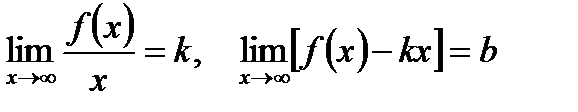, то прямая  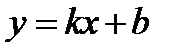является наклонной асимптотой графика функции).

6. Найти экстремумы и промежутки монотонности функции:

- найти производную функции,

- найти критические точки функции, в которых производная равна нулю или не существует,

- исследовать знаки производной слева и справа от каждой критической точки и сделать вывод о характере монотонности и наличии экстремумов функции (если производная на некотором интервале принимает положительные значения, то функция на этом интервале возрастает; если производная отрицательна, то функция убывает; если при переходе через критическую точку производная функции меняет свой знак с минуса на плюс, то данная точка является точкой минимума; если при переходе через критическую точку производная функции меняет свой знак с плюса на минус, то данная точка является точкой максимума).

7. Найти интервалы выпуклости функции и точки перегиба:

- найти вторую производную функции ,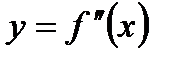

- найти точки, в которых вторая производная равна нулю или не существует,

- исследовать знаки второй производной слева и справа от каждой из найденных точек и сделать вывод об интервалах выпуклости и наличии точек перегиба функции (если вторая производная функции на некотором интервале положительна, то функция выпукла вниз на этом интервале; если вторая производная функции на некотором интервале отрицательна, то функция выпукла вверх на этом интервале; если вторая производная при переходе через некоторую точку меняет свой знак, то эта точка является точкой перегиба).

- найти значения функций в точках перегиба.

8. Найти точки пересечения с осями координат, промежутки знакопостоянства и, возможно, некоторые дополнительные точки, уточняющие график.

Схема может варьироваться (например, для тригонометрических функций вводится исследование на периодичность), ее «шаги» могут меняться местами, однако их смысл при этом не меняется.