Нижнетагильский машиностроительный техникум
УТВЕРЖДАЮ
Директор техникума
____________ В.В. Потанин
« ___»_____________2015 г.
Методические рекомендации
по выполнению домашней контрольной работы
для студентов заочной формы обучения
по учебной дисциплине «Математика»
специальность 22.02.03
Литейное производство черных и цветных металлов
Нижний Тагил,
2015
Методические рекомендации разработаны на основе Федерального государственного образовательного стандарта (далее ФГОС) (регистрационный № 357, от 21.04.14) по специальности среднего профессионального образования (далее СПО) 22.02.03 Литейное производство черных и цветных металлов (базовой подготовки), рабочей программы учебной дисциплины «Математика».
| Организация разработчик: | ФГАОУ ВПО «Уральский федеральный университет имени первого Президента России Б.Н. Ельцина» Нижнетагильский технологический и институт Нижнетагильский машиностроительный техникум |
| Разработчик: | преподаватель НТМТ Ведерникова Е.В. |
Методические рекомендации обсуждены и одобрены на заседании цикловой комиссии общеобразовательного, социально-экономического, математического и естественнонаучного цикла
| Протокол № ___________ «____» _________ 2015 г. | Председатель ЦК Ведерникова Е.В. |
Методические рекомендации рассмотрены и ободрены на заседании и Методического Совета НТМТ
| Протокол № ___________ «____» _________ 2015 г. | Председатель Методического Совета _________________ В.В. Потанин |
Содержание
| Введение | |
| 1. Пояснительная записка | |
| 1.1 Результаты освоения учебной дисциплины. | |
| 1.2 Основные понятия, необходимые для выполнения ДКР. | |
| 1.3 Примеры решения упражнений. | |
| 2. Задания для домашней контрольной работы | |
| 3. Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы. |
Введение
Цель методических рекомендаций - помочь студентам освоить курс математики.
В методических указаниях кратко излагаются узловые теоретические вопросы, без знания которых нельзя выполнить домашнюю контрольную работу (ДКР).
В методических указаниях приведены примеры решения упражнений по изучаемым темам курса.
Приведен список учебно-методической и нормативно-правовой литературы, необходимой для успешного выполнения ДКР и освоения учебной программы.
Студентам предлагается для выполнения ДКР, состоящую из десяти вариантов, каждый из которых содержит шесть упражнений по изучаемым темам курс математики. Кроме того, для самостоятельного изучения выдаются темы, включенные в экзаменационные билеты.
Пояснительная записка
1.1 Результаты освоения дисциплины «Математика».
Тематический план и содержание учебной дисциплины соответствует рабочей программе учебной дисциплины «Математика».
С целью формирования элементов соответствующих общих и профессиональных компетенций обучающийся в ходе освоения учебной дисциплины должен
уметь:
- анализировать сложные функции и строить их графики;
- выполнять действия над комплексными числами;
- вычислять значения геометрических величин;
- производить операции над матрицами и определителями;
- решать задачи на вычисление вероятности с использованием элементов комбинаторики;
- решать прикладные задачи с использованием элементов дифференциального и интегрального исчислений;
- решать системы линейных уравнений различными методами.
знать:
- основные математические методы решения прикладных задач;
- основные понятия и методы математического анализа, линейной алгебры, теорию комплексных чисел, теории вероятностей и математической статистики;
- основы интегрального и дифференциального исчисления;
- роль и место математики в современном мире при освоении профессиональных дисциплин и в сфере профессиональной деятельности.
Результатом освоения программы учебной дисциплины является овладение обучающимися профессиональными (ПК) и общими (ОК) компетенциями:
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
ОК 5. Использовать информационно – коммуникационные технологии в профессиональной деятельности.
ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.
ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.
ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности.
ПК 1.3. Выполнять расчёты, необходимые при разработке технологических процессов изготовления отливок
ПК 3.3. Рассчитывать основные технико-экономические показатели работы коллектива,
осуществляется в части следующих результатов обучения.
Основные понятия, необходимые для выполнения ДКР
Теория пределов
Определение предела функции в точке
Сформулируем определение предела функции в точке.
Определение. Пусть функция f( x) определена в некоторой окрестности точки а, кроме, может быть, самой точки а, Число В называется пределом функции f( x) в точке а (или при х, стремящемся к а), если для любой последовательности значений аргумента хп ¹ а, п Î N, сходящейся к а, последовательность соответствующих значений функции f( xп), п Î N, сходится к числу В.
В этом случае пишут: 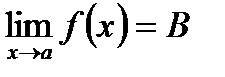 или
или 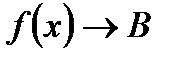 при
при 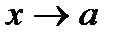 .
.
Если же для некоторой последовательности значений аргумента, сходящейся к а, соответствующая последовательность значений функции не является сходящейся, то функция в данной точке не имеет предела. То же заключение можно сделать, если для двух различных последовательностей значений аргумента последовательности соответствующих значений функции имеют различные пределы.
Очевидно, число В является пределом функции 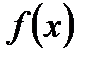 при
при 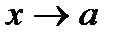 тогда и только тогда, когда
тогда и только тогда, когда 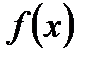 можно представить в виде:
можно представить в виде:
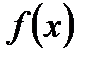 = В +
= В + 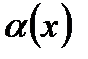 , где
, где 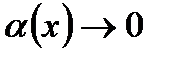 при
при 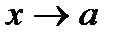 .
.
Отметим, что точка а, в которой рассматривается предел функции 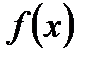 , может принадлежать области определения функции
, может принадлежать области определения функции 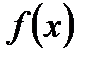 , а может и не принадлежать. При нахождении предела функции в точке не рассматривается значение функции в этой точке.
, а может и не принадлежать. При нахождении предела функции в точке не рассматривается значение функции в этой точке.
Свойства пределов функций
Основные свойства пределов функций аналогичны теоремам о пределах числовых последовательностей:
1) Предел суммы (разности) функций равен сумме (разности) их пределов, если последние существуют: 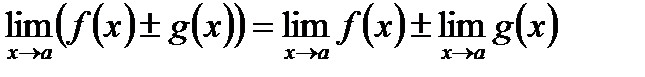 .
.
2) Предел произведения функций равен произведению их пределов, если последние существуют: 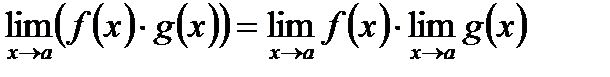 .
.
Следствие. Постоянный множитель можно выносить за знак предела: 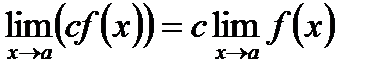 , если
, если 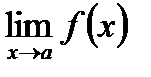 существует.
существует.
3) Предел отношения двух функций равен отношению их пределов, если последние существуют и предел делителя отличен от нуля: 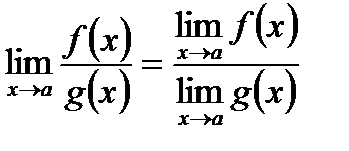 , если
, если 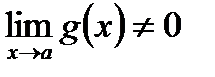 .
.
При изучении пределов функций иногда полезно использовать следующую «теорему о пределе промежуточной функции».
Теорема. Если 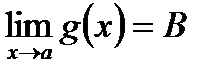 ,
, 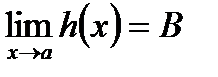 и в некоторой окрестности точки а, кроме, быть может, самой точки а, выполняются неравенства
и в некоторой окрестности точки а, кроме, быть может, самой точки а, выполняются неравенства 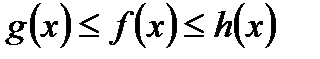 , то
, то 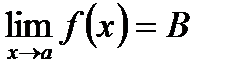 .
.
Производная сложной функции
Определение производной
Рассмотрим функцию 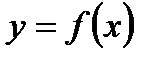 , где
, где 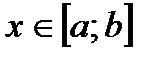 (рис. 31). Возьмем произвольную точку
(рис. 31). Возьмем произвольную точку 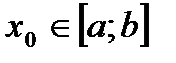 . Для любого
. Для любого 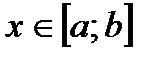 разность х – х0 называется приращением аргумента х в точке х0 и обозначается
разность х – х0 называется приращением аргумента х в точке х0 и обозначается 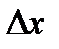 . Таким образом,
. Таким образом,
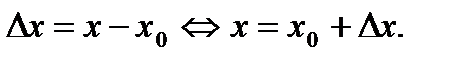
Разность 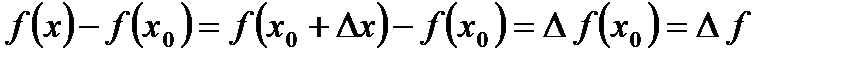 называется приращением функции в точке х0.
называется приращением функции в точке х0.
Производной функции 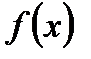 в точке х0 называется предел отношения приращения функции
в точке х0 называется предел отношения приращения функции 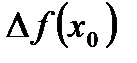 к приращению аргумента
к приращению аргумента 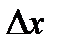 при
при 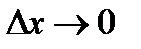 , если этот предел существует и обозначается
, если этот предел существует и обозначается 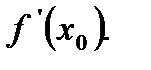
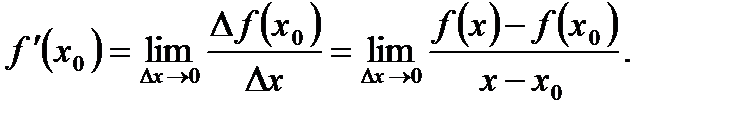
Функция, имеющая производную в точке х0, называется дифференцируемой в этой точке. Если же функция дифференцируема в каждой точке некоторого интервала 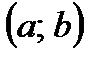 , то она дифференцируема на этом интервале. Необходимое условие существования производной вытекает из следующей теоремы.
, то она дифференцируема на этом интервале. Необходимое условие существования производной вытекает из следующей теоремы.
Теорема. Если функция 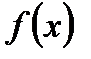 дифференцируема в точке х0, то она непрерывна в этой точке.
дифференцируема в точке х0, то она непрерывна в этой точке.
Однако непрерывность функции в точке не является достаточным условием дифференцируемости функции в точке.
Правила дифференцирования
Если функции u(x) и v(x) имеют производные во всех точках интервала
(a; b) , то для любого х Î (a; b) выполняются следующие равенства:
1. 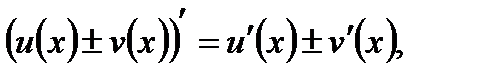
2. 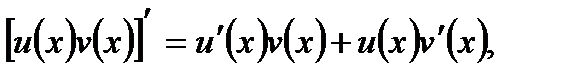
3. 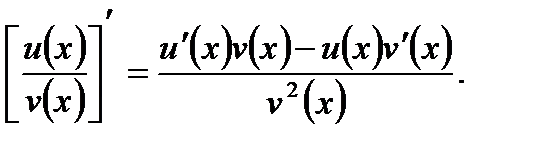
Следствие. Постоянный множитель можно выносить за знак производной:

Формулы дифференцирования
| № п/п | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
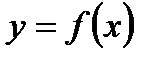
| C | х | хп | 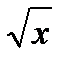
| 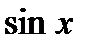
| 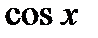
| 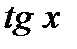
| 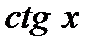
| ex | ax |
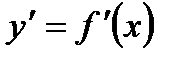
| 0 | 1 | nxn-1 | 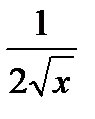
| cosx | -sin x | 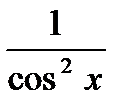
| 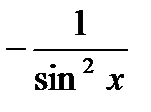
| ex | ax 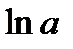
|
| № п/п | 11 | 12 | 13 | 14 | 15 | 16 |
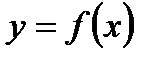
| 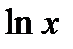
| 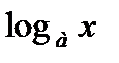
| arcsinx | arccosx | arctgx | arcctgx |
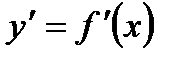
| 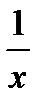
| 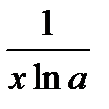
| 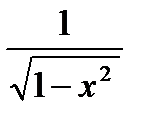
| 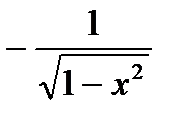
| 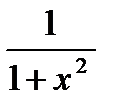
| 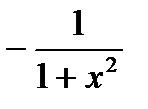
|
Производная сложной функции
С понятием сложной функции Вы уже неоднократно сталкивались в школьном курсе математики. Пусть даны две функции 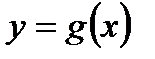 и
и 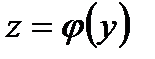 , причем область определения функции
, причем область определения функции 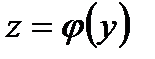 содержит область значений функции
содержит область значений функции 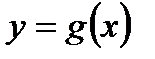 .
.
Функция, заданная формулой 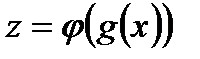 , называется сложной функцией, составленной из функций g и j или суперпозицией функций g и j.
, называется сложной функцией, составленной из функций g и j или суперпозицией функций g и j.
Дифференциал
Дифференциал 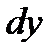 функции
функции 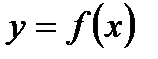 – это главная часть приращения функции
– это главная часть приращения функции 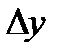 в точке х, так что
в точке х, так что 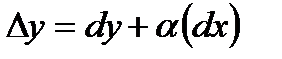 , где
, где 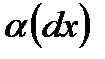 – бесконечно малая величина.
– бесконечно малая величина.
Дифференциал функции 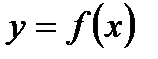 вычисляется по формуле:
вычисляется по формуле:
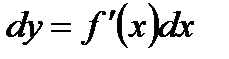 ,
,
где 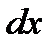 – дифференциал аргумента, равный приращению аргумента в данной точке.
– дифференциал аргумента, равный приращению аргумента в данной точке.
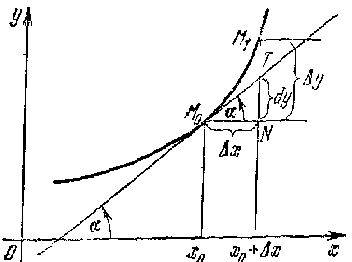
| Геометрический смысл дифференциала: дифференциал функции равен приращению ординаты касательной к графику функции в соответствующей точке, когда аргумент получает приращение 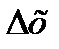 (см. рис. 8).
Приближенное равенство (см. рис. 8).
Приближенное равенство 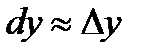 используется в приближенных вычислениях. В таких случаях значение выражения используется в приближенных вычислениях. В таких случаях значение выражения 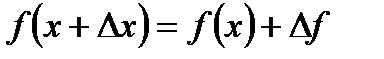 заменяют приближением: заменяют приближением: 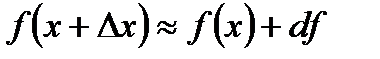
|
Таблица интегралов.
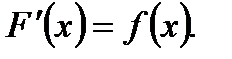 .
.
Свойство первообразной.
Если F1(x) и F2(x) – первообразные для функции f(x) в некотором промежутке Х, то найдется такое число С, что справедливо равенство: 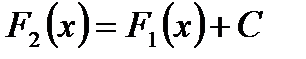 .
.
Совокупность всех первообразных для функции f(x) на промежутке Х называется неопределенным интегралом от функции f(x) и обозначается 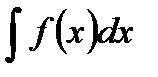 .
.
Согласно определению,  .
.
Свойства неопределенного интеграла.
- Производная от неопределенного интеграла равна подынтегральной функции:
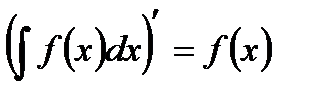 .
. - Дифференциал неопределенного интеграла равен подынтегральному выражению:
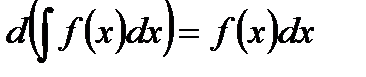 .
. - Неопределенный интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого:
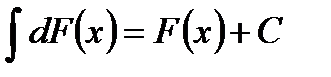 .
. - Постоянный множитель можно выносить за знак интеграла:
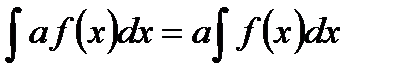 .
. - Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций:
-
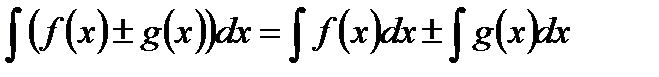 .
.
Таблица интегралов:
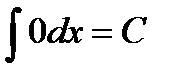 ;
; 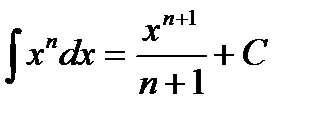 (при п ¹ –1);
(при п ¹ –1); 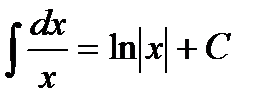 ;
;
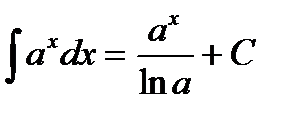 (при а > 0, a ¹ 0);
(при а > 0, a ¹ 0);
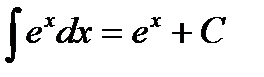 ;
; 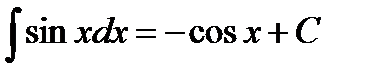 ;
; 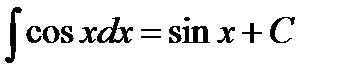 ;
;
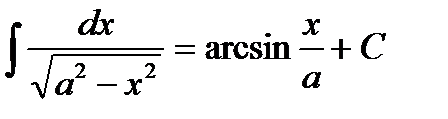 (при
(при 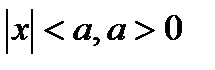 );
);
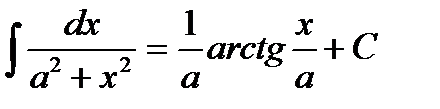 (при a ¹ 0);
(при a ¹ 0);
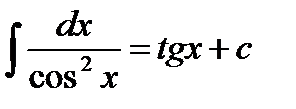
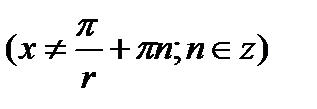 ;
;
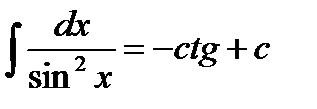
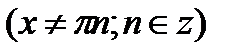 ;
;
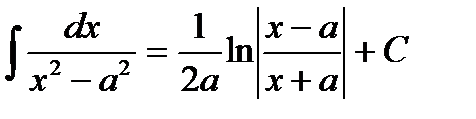 (при a ¹ 0);
(при a ¹ 0); 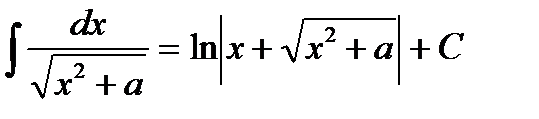 .
.
Определенный интеграл
Пусть предел интегральной суммы при стремлении 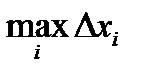 к нулю существует, конечен и не зависит от способа выбора точек х1, х2,… и точек x1, x2,… Тогда этот предел называется определенным интегралом от функции у=f(x) на [a; b], обозначается
к нулю существует, конечен и не зависит от способа выбора точек х1, х2,… и точек x1, x2,… Тогда этот предел называется определенным интегралом от функции у=f(x) на [a; b], обозначается 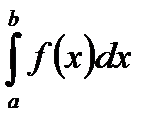 , а сама функция у = f(x) называется интегрируемой на [a; b], т.е.
, а сама функция у = f(x) называется интегрируемой на [a; b], т.е.
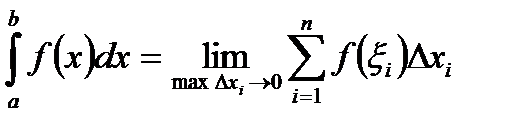 .
.
Свойства определенного интеграла:
1. Постоянный множитель можно выносить за знак интеграла:
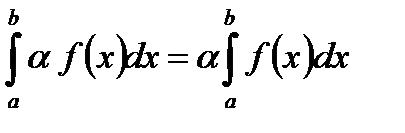 .
.
2. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций: 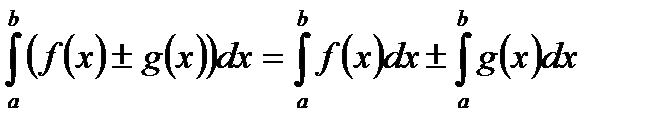
3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е.
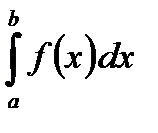
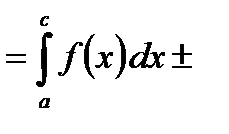
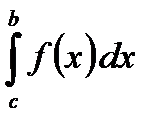 .
.
4. Если на отрезке [a; b] f(x) £ g(x), то и 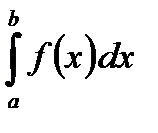 £
£ 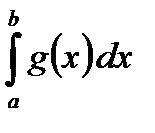 .
.
5. Если функция у = f(x) непрерывна на отрезке [a; b], то найдется такое значение x Î [a; b], что 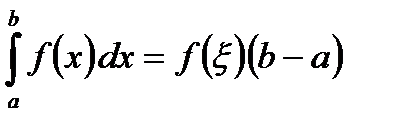 .
.
Формула Ньютона-Лейбница.
Пусть функция у = f(x) непрерывна на отрезке [a; b] и F(x) первообразная функцией для функции f(x) на отрезке [a; b]. Тогда определенный интеграл от функции f(x) на [a; b] равен приращению первообразной на этом отрезке, т.е. 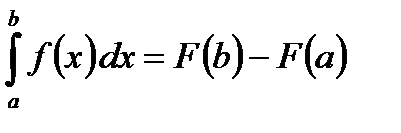 .
.
Ряды.
Основные понятия
Числовым рядом называется сумма вида
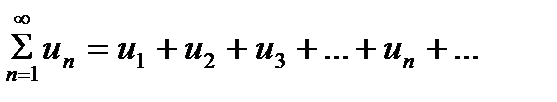
Где числа u1, u2, u3, …. , un, … называемые членами ряда, образуют бесконечную последовательность; член un называют общим членом ряда.
Суммы:

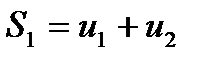
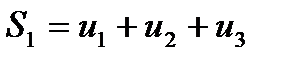
. . . . . . . . . . .

составленные из первых членов ряда, называются частичными суммами этого ряда.
Каждому ряду можно сопоставить последовательность частичных сумм S1, S2, S3,…., Sn Если при бесконечном возрастании номера n частичная сумма ряда Sn стремится к пределу S, то ряд называется сходящимся, а число S – суммой сходящегося ряда, т.е.
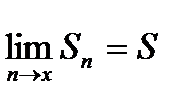 или
или 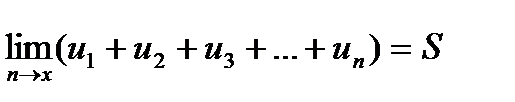
Эта запись равносильна записи
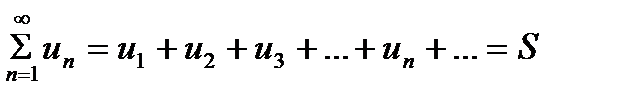
Если частичная сумма Sn ряда при неограниченном возрастании n не имеет конечного предела ( в частности, стремится к +х или к – бесконечность), то такой ряд называют расходящимся.
Если ряд сходится, то значение Sn при достаточно большом n является приближенным выражением суммы ряда S.
Разность rn = S - Sn называется остатком ряда. Если ряд сходится, то его остаток стремится к нулю, т.е. 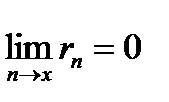 , и наоборот, если остаток стремится к нулю, то ряд сходится.
, и наоборот, если остаток стремится к нулю, то ряд сходится.
Пример 2.
Найдем производные следующих функций:
1) 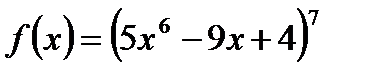 ;
;
2) 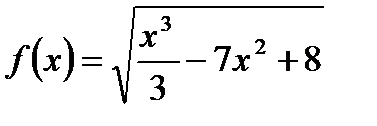 ;
;
3) 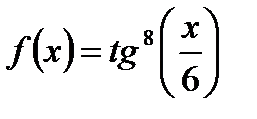 .
.
Решение.
1) Полагаем, что 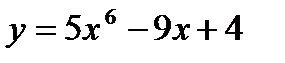 , тогда
, тогда 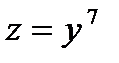 . Отсюда, согласно формуле для расчета производной сложной функции, имеем:
. Отсюда, согласно формуле для расчета производной сложной функции, имеем:
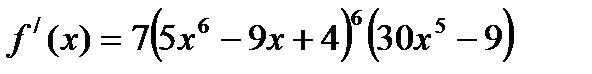 .
.
2) Полагаем, что 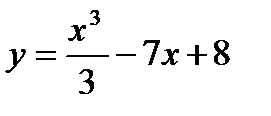 , тогда
, тогда 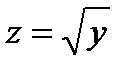 . Отсюда, согласно формуле для расчета производной сложной функции, имеем:
. Отсюда, согласно формуле для расчета производной сложной функции, имеем:
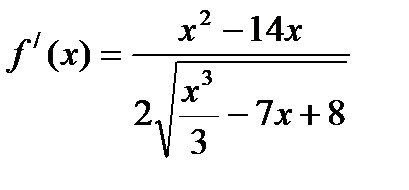 .
.
3) Имеем, что
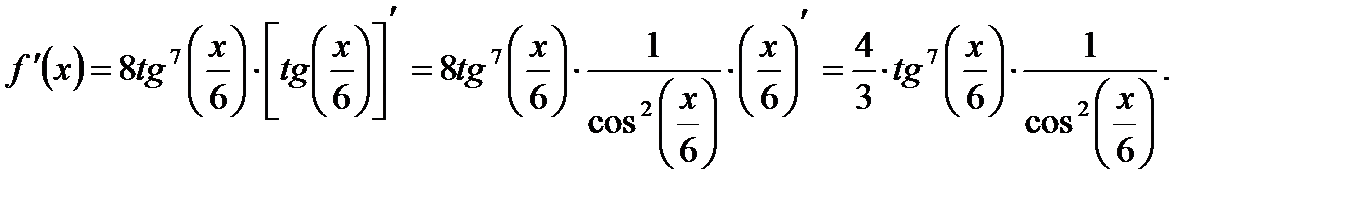
Пример 3.
Исследуем функцию и построим эскиз ее графика:
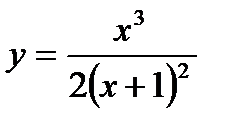
Решение.
1. Определим область существования этой функции. Функция существует при всех значениях х, кроме 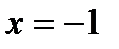 , при котором знаменатель дроби обращается в нуль. Значит, функция определена в интервалах (—
, при котором знаменатель дроби обращается в нуль. Значит, функция определена в интервалах (— 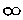 , —1)
, —1) 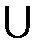 (—1, +
(—1, + 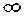 ).
).
2. Исследуем вопрос о наличии центра симметрии к оси симметрии. Проверим для этого, выполняются ли равенства 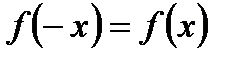 или
или 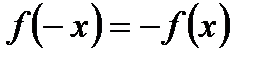 .
.
Непосредственная подстановка убеждает нас, что ни одно из этих равенств не выполняется, так что ни центра, ни оси симметрии график функции не имеет.
3. Определяем точки разрыва. Числитель и знаменатель дробно-рациональной функции 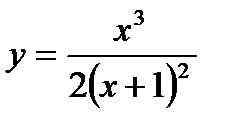 представляют собой непрерывные функции и, следовательно, функция у будет непрерывной при всех значениях х, кроме
представляют собой непрерывные функции и, следовательно, функция у будет непрерывной при всех значениях х, кроме 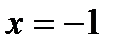 , при котором знаменатель дроби обращается в нуль.
, при котором знаменатель дроби обращается в нуль.
4. Переходим к определению асимптот графика.
а) Вертикальные асимптоты найдем, приравняв знаменатель нулю:
2(х+1)2 = 0; отсюда 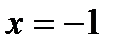 .
.
Вертикальная асимптота одна: ее уравнение 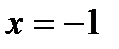 .
.
б) Горизонтальные асимптоты находим так: отыскиваем
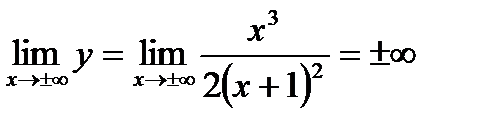 ,
,
а это означает, что горизонтальных асимптот нет.
в) Наклонные асимптоты:
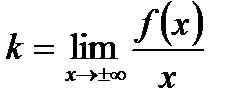
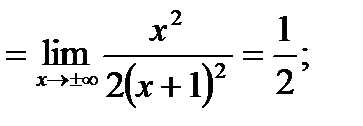
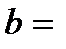
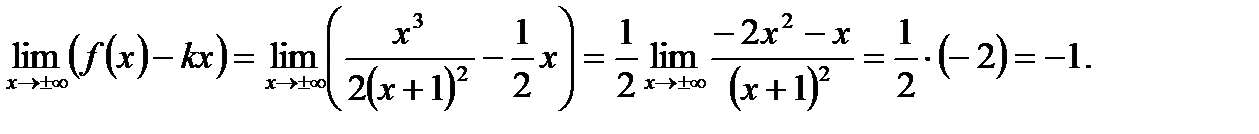
Наклонная асимптота одна: 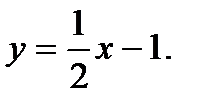
5 и 6. Определяем интервалы возрастания и убывания функции и экстремум функции.
Находим первую производную: 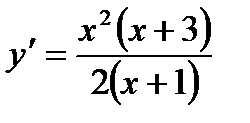 . Определим критические точки:
. Определим критические точки:
1) Решаем уравнение 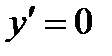 , т. е. уравнение
, т. е. уравнение 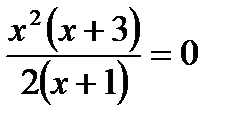 и находим, что
и находим, что 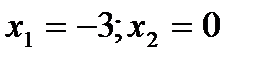 .
.
2) Определяем значения х, при которых 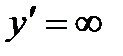 . Таким значением является
. Таким значением является 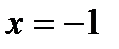 Но это значение не должно подлежать рассмотрению, так как оно не входит в область определения функции. Критические точки, подлежащие рассмотрению:
Но это значение не должно подлежать рассмотрению, так как оно не входит в область определения функции. Критические точки, подлежащие рассмотрению: 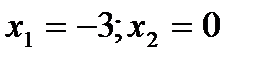 и точка
и точка 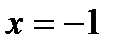 – разделяют область существования функции на такие интервалы:
– разделяют область существования функции на такие интервалы: 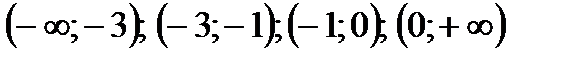 .
.
В каждом из этих интервалов производная сохраняет знак: в первом — плюс, во втором — минус, в третьем — плюс, в четвертом — плюс (в этом можно убедиться, взяв в каждом интервале произвольное значение х и вычислив при нем значение у'). Последовательность знаков первой производной запишется так: +, —, +, +. Значит, в интервале 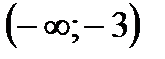 функция возрастает, в интервале
функция возрастает, в интервале 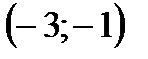 – убывает, в интервалах
– убывает, в интервалах 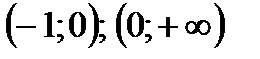 функция возрастает.
функция возрастает.
При 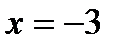 функция имеет максимум и
функция имеет максимум и 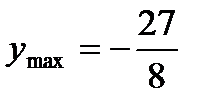 . Так как знаки во втором и третьем интервалах различны, то можно было бы предположить, что при
. Так как знаки во втором и третьем интервалах различны, то можно было бы предположить, что при  есть экстремум. Но такое предположение неверно, так как при
есть экстремум. Но такое предположение неверно, так как при 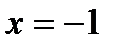 заданная функция не существует. Итак, функция имеет единственный экстремум (максимум) при
заданная функция не существует. Итак, функция имеет единственный экстремум (максимум) при 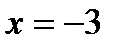 .
.
7. Определяем интервалы выпуклости и вогнутости графика функции и точек перегиба.
Находим, что 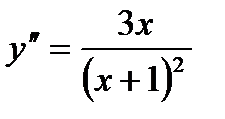 и определяем критические точки второго рода:
и определяем критические точки второго рода:
1) решаем уравнение 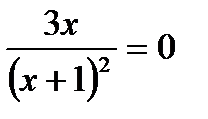 и находим, что
и находим, что 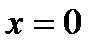 ;
;
2) определяем значения х, при котором 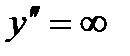 . Таким значением является
. Таким значением является 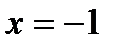 . Как уже было отмечено выше, это значение рассматриваться не должно, так как при нем не существует заданной функции.
. Как уже было отмечено выше, это значение рассматриваться не должно, так как при нем не существует заданной функции.
Критическая точка второго рода 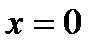 разделяет интервалы (—
разделяет интервалы (— 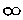 , —1) и (—1, +
, —1) и (—1, + 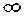 ). существования функции на интервалы:
). существования функции на интервалы: 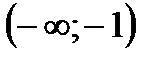 ,
, 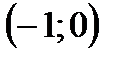 и
и 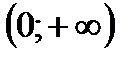 .
.
В каждом из этих интервалов вторая производная конечна и сохраняет знак: в первом – минус, во втором – минус, в третьем – плюс, и мы имеем такое чередование знаков второй производной в этих интервалах: —, —, +.
Значит, в интервалах 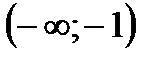 и
и 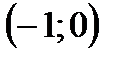 кривая выпукла, а в интервале
кривая выпукла, а в интервале
(0, + ∞) — вогнута. При 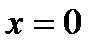 вторая производная равна нулю, а при переходе из второго интервала в третий она поменяла знак. Это указывает на то, что при
вторая производная равна нулю, а при переходе из второго интервала в третий она поменяла знак. Это указывает на то, что при 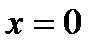 , кривая имеет точку перегиба. Координаты точки перегиба (0, 0) — это начало координат.
, кривая имеет точку перегиба. Координаты точки перегиба (0, 0) — это начало координат.
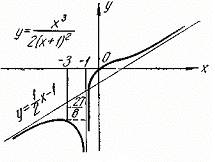 Рис. 9 Рис. 9
| 8. Определение точек пересечения графика с осями координат и исследование промежутков монотонности произведите самостоятельно. График функции пересекает оси координат в единственной точке 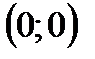 . Функция отрицательна на промежутках . Функция отрицательна на промежутках 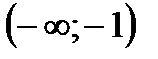 и и 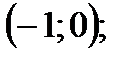 положительна на промежутке положительна на промежутке 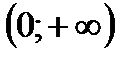 . .
|
Все полученные сведения наносим на чертеж и получаем эскиз кривой (см. рис. 9).
Пример 4.
Найдем 1) 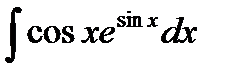 , 2)
, 2) 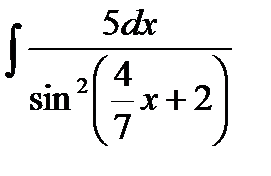
Решение.
1)
| . |
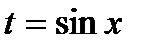 . Тогда
. Тогда 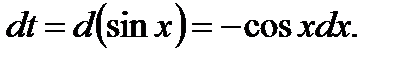
Произведя подстановку, получим:
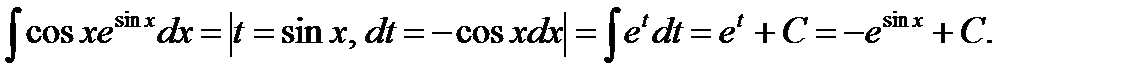
2) Так как аргумент подынтегральной функции имеет вид 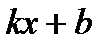 , где
, где 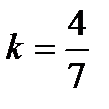 , то, применяя вышеназванную теорему, получим:
, то, применяя вышеназванную теорему, получим:

Пример 5.
Вычислим 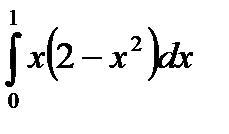 .
.
Решение.
Положим 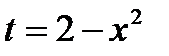 . Тогда
. Тогда 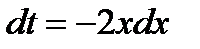 . Вычислим значения новых пределов интегрирования, подставив в формулу новой переменной исходные значения пределов:
. Вычислим значения новых пределов интегрирования, подставив в формулу новой переменной исходные значения пределов: 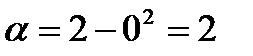 ,
, 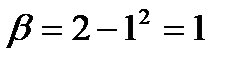 . Воспользовавшись формулой замены переменной в определенном интеграле, получим:
. Воспользовавшись формулой замены переменной в определенном интеграле, получим:
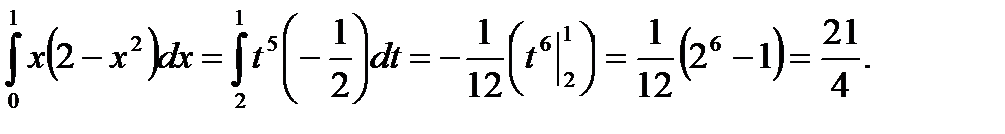
Пример 6.
Исследовать сходимость ряда, используя признак Даламбера:
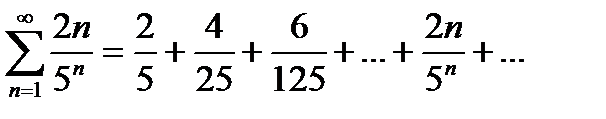
Решение. Подставив в общий член ряда  вместо n число n+1, получим
вместо n число n+1, получим 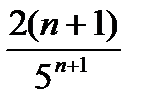 . Найдём предел отношения (n+1)-ого члена к n-му члену при
. Найдём предел отношения (n+1)-ого члена к n-му члену при 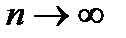 :
:
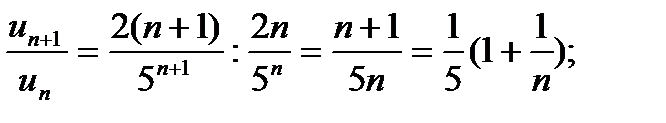
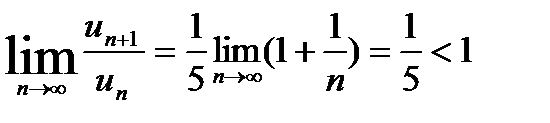 .
.
Следовательно, данный ряд сходится.
Задания для контрольной работы
Для получения аттестации по учебной дисциплине «Математика» необходимо выполнить домашнюю контрольную работу, сдать экзамен.
Разделы, изучаемые в учебной дисциплине «Математика»
1. Математический анализ
2. Основы теории комплексных чисел
3. Основы теории вероятностей
4. Основные численные методы.
Методические указания для выполнения ДКР:
· ДКР состоит из 6 заданий. Количество вариантов 10.
· Номер варианта выбирается по двум последним цифрам студенческого билета.
· Текст практических заданий необходимо переписать.
· Обязательно написание всех формул с последующей расшифровкой букв и символов.
· Работа выполняется в тетради вручную или в печатном варианте. Отдельные листы необходимо скрепить.
· На проверку ДКР сдается не позднее двух недель до начала сессии. В случае возврата преподавателем выполненной ДКР, ошибки исправляются в этой же тетради, первый отзыв должен быть приложен к работе.
Контрольная работа засчитывается, если соблюдены все требования и все задания выполнены верно.
Желаем Вам успехов в самостоятельном изучении материала
и решении предложенных задач!
Задания для ДКР
Вариант 1
1) Вычислите предел функции: 
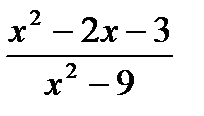
2) Найдите производную функции при данном значении аргумента: f(x) = 2sin2x; f/( 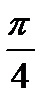 )
)
3) Найдите экстремумы функции: y = 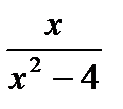
4) Найдите неопределенный интеграл: 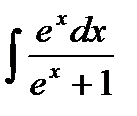
5) Вычислите: 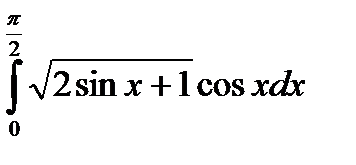 .
.
6) Используя признак Даламбера, исследовать на сходимость ряд: 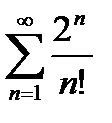
Вариант 2
1) Вычислите предел функции: 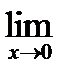
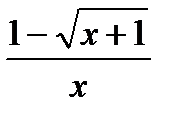
2) Найдите производную функции при данном значении аргумента: f(x) = 3cos2x; f/(- 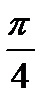 )
)
3) Найдите экстремумы функции: y = 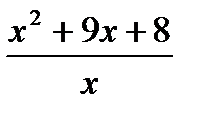
4) Найдите неопределенный интеграл: 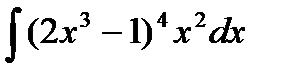
5) Вычислите: 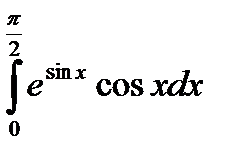 .
.
6) Используя признак Даламбера, исследовать на сходимость ряд: 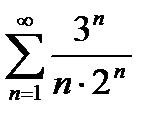
Вариант 3
1) Вычислите предел функции: 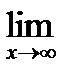
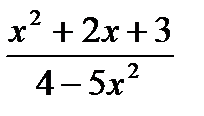
2) Найдите производную функции при данном значении аргумента: f(x) = ln(cosx); f/( 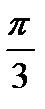 )
)
3) Найдите экстремумы функции: y = 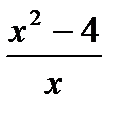
4) Найдите неопределенный интеграл: 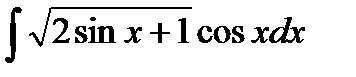
5) Вычислите: 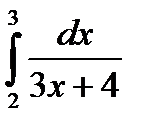
6) Используя признак Даламбера, исследовать на сходимость ряд: 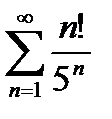
Вариант 4
1) Вычислите предел функции: 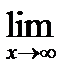 (1+
(1+ 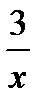 )x
)x
2) Найдите производную функции при данном значении аргумента: f(x) = ln(sinx); f/( 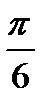 )
)
3) Найдите экстремумы функции: y = 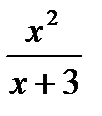
4) Найдите неопределенный интеграл: 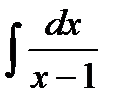
5) Вычислите: 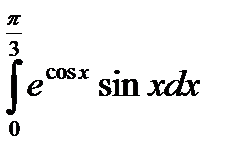
6) Используя признак Даламбера, исследовать на сходимость ряд: 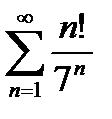
Вариант 5
1) Вычислите предел функции: 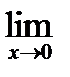
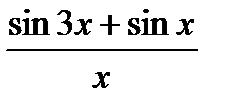
2) Найдите производную функции при данном значении аргумента: f(x) = 4cos2x); f/( 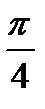 )
)
3) Найдите экстремумы функции: y = 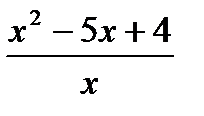
4) Найдите неопределенный интеграл: 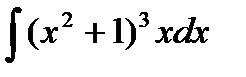 .
.
5) Вычислите: 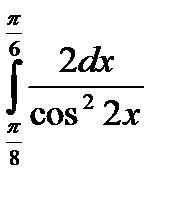
6) Используя признак Даламбера, исследовать на сходимость ряд: 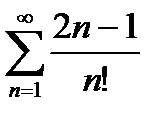
Вариант 6
1) Вычислите предел функции: 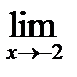
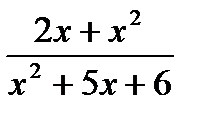
2) Найдите производную функции при данном значении аргумента: f(x) = ln 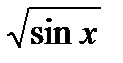 ; f/(
; f/( 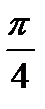 )
)
3) Найдите экстремумы функции: y = 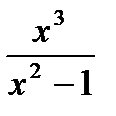
4) Найдите неопределенный интеграл: 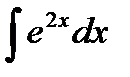 .
.
5) Вычислите: 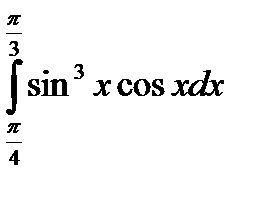
6) Используя признак Даламбера, исследовать на сходимость ряд: 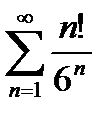
Вариант 7
1) Вычислите предел функции: 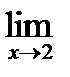
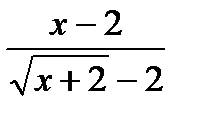
2) Найдите производную функции при данном значении аргумента: f(x) = arctg 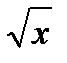 ; f/(
; f/( 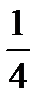 )
)
3) Найдите экстремумы функции: y = 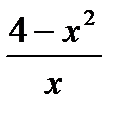
4) Найдите неопределенный интеграл: 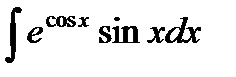
5) Вычислите: 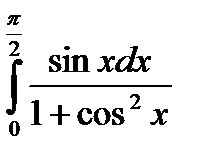 .
.
6) Используя признак Даламбера, исследовать на сходимость ряд: 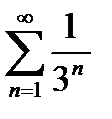
Вариант 8
1) Вычислите предел функции: 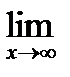
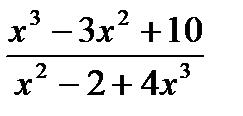
2) Найдите производную функции при данном значении аргумента: f(x) = e 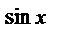 ; f/(0)
; f/(0)
3) Найдите экстремумы функции: y = 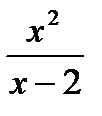
4) Найдите неопределенный интеграл: 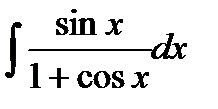
5) Вычислите: 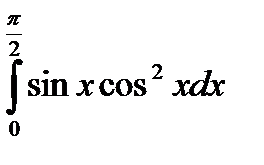
6) Используя признак Даламбера, исследовать на сходимость ряд: 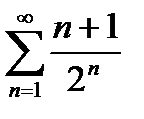
Вариант 9
1) Вычислите предел функции: 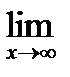 (1-
(1- 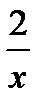 )x
)x
2) Найдите производную функции при данном значении аргумента: f(x) = e 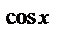 ; f/(
; f/( 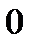 )
)
3) Найдите экстремумы функции: y = 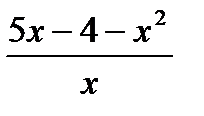
4) Найдите неопределенный интеграл: 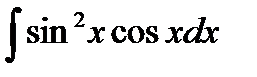
5) Вычислите: 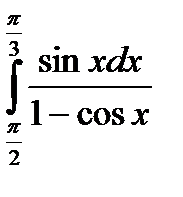
6) Используя признак Даламбера, исследовать на сходимость ряд: 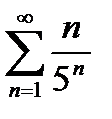
Вариант 10
1) Вычислите предел функции: 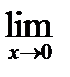
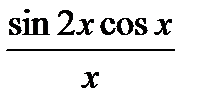 .
.
2) Найдите производную функции при данном значении аргумента: f(x) = cos2x2; f/( 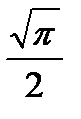 )
)
3) Найдите экстремумы функции: y = 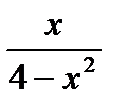
4) Найдите неопределенный интеграл: 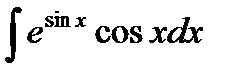
5) Вычислите: 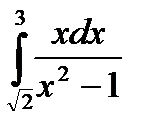
6) Используя признак Даламбера, исследовать на сходимость ряд: 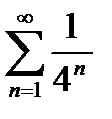
3. Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы
Основные источники:
1. Богомолов Н.Б. Практические занятия по математике: учебное пособие для студентов средних специальных учебных заведений. Высш. шк., 2007
2. Богомолов Н.Б., П.И.Самойленко Математика: учебник для студентов образовательных учреждений среднего профессионального образования. Дрофа, 2006
3. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учебное пособие 2007.
4. Гмурман В.Е. Теория вероятностей и математическая статистика.
5. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в
упражнениях и задачах (в двух частях), 2006г.
6. Лапчук М.П, М.И.Рагулина, Е.К.Хеннер Численные методы: учебное пособие Издательский центр «Академия», 2007
7. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие для студентов образовательных учреждений среднего профессионального образования. – Ростов н/Д: Феникс, 2007
8. Спирина М.С., Спирин П.А. Дискретная математика: учебник для студентов образовательных учреждений среднего профессионального образования. Издательский центр «Академия», 2007.
Дополнительные источники:
1. Вентцель. Е.С. Теория вероятностей образования учебник для студентов высших учебных заведений. Издательский центр «Академия», 2005
2. Григорьев В.П., Ю.А.Дубинский Элементы высшей математики: учебник для студентов образовательных учреждений среднего профессионального образования. Издательский центр «Академия», 2004
3. Саакян С.М., А.М.Гольдман, Д.В.Денисов Задачи по алгебре и началам анализа: пособие для учащихся 10 – 11 кл. Просвещение, 2005
4. Шипачев С.М. Начала высшей математики: пособие для вузов. Дрофа, 2002
Интернет-ресурсы:
1. http://en.edu/ru – естественнонаучный портал;
2. http://schools.techno.ru – сайт «Школы в Интернете»
3. http://www.school.edu.ru – российский образовательный портал
4. http://www.alleng.ru- сайт «Образовательные ресурсы Интернета школьникам и студентам и др.
Нижнетагильский машиностроительный техникум
УТВЕРЖДАЮ
Директор техникума
____________ В.В. Потанин
« ___»_____________2015 г.
Методические рекомендации
по выполнению домашней контрольной работы
для студентов заочной формы обучения
по учебной дисциплине «Математика»
специальность 22.02.03
Литейное производство черных и цветных металлов
Нижний Тагил,
2015
Методические рекомендации разработаны на основе Федерального государственного образовательного стандарта (далее ФГОС) (регистрационный № 357, от 21.04.14) по специальности среднего профессионального образования (далее СПО) 22.02.03 Литейное производство черных и цветных металлов (базовой подготовки), рабочей программы учебной дисциплины «Математика».
| Организация разработчик: | ФГАОУ ВПО «Уральский федеральный университет имени первого Президента России Б.Н. Ельцина» Нижнетагильский технологический и институт Нижнетагильский машиностроительный техникум |
| Разработчик: | преподаватель НТМТ Ведерникова Е.В. |
Методические рекомендации обсуждены и одобрены на заседании цикловой комиссии общеобразовательного, социально-экономического, математического и естественнонаучного цикла
| Протокол № ___________ «____» _________ 2015 г. | Председатель ЦК Ведерникова Е.В. |
Методические рекомендации рассмотрены и ободрены на заседании и Методического Совета НТМТ
| Протокол № ___________ «____» _________ 2015 г. | Председатель Методического Совета _________________ В.В. Потанин |
Содержание
| Введение | |
| 1. Пояснительная записка | |
| 1.1 Результаты освоения учебной дисциплины. | |
| 1.2 Основные понятия, необходимые для выполнения ДКР. | |
| 1.3 Примеры решения упражнений. | |
| 2. Задания для домашней контрольной работы | |
| 3. Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы. |
Введение
Цель методических рекомендаций - помочь студентам освоить курс математики.
В методических указаниях кратко излагаются узловые теоретические вопросы, без знания которых нельзя выполнить домашнюю контрольную работу (ДКР).
В методических указаниях приведены примеры решения упражнений по изучаемым темам курса.
Приведен список учебно-методической и нормативно-правовой литературы, необходимой для успешного выполнения ДКР и освоения учебной программы.
Студентам предлагается для выполнения ДКР, состоящую из десяти вариантов, каждый из которых содержит шесть упражнений по изучаемым темам курс математики. Кроме того, для самостоятельного изучения выдаются темы, включенные в экзаменационные билеты.
Пояснительная записка
1.1 Результаты освоения дисциплины «Математика».
Тематический план и содержание учебной дисциплины соответствует рабочей программе учебной дисциплины «Математика».
С целью формирования элементов соответствующих общих и профессиональных компетенций обучающийся в ходе освоения учебной дисциплины должен
уметь:
- анализировать сложные функции и строить их графики;
- выполнять действия над комплексными числами;
- вычислять значения геометрических величин;
- производить операции над матрицами и определителями;
- решать задачи на вычисление вероятности с использованием элементов комбинаторики;
- решать прикладные задачи с использованием элементов дифференциального и интегрального исчислений;
- решать системы линейных уравнений различными методами.
знать:
- основные математические методы решения прикладных задач;
- основные понятия и методы математического анализа, линейной алгебры, теорию комплексных чисел, теории вероятностей и математической статистики;
- основы интегрального и дифференциального исчисления;
- роль и место математики в современном мире при освоении профессиональных дисциплин и в сфере профессиональной деятельности.
Результатом освоения программы учебной дисциплины является овладение обучающимися профессиональными (ПК) и общими (ОК) компетенциями:
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
ОК 5. Использовать информационно – коммуникационные технологии в профессиональной деятельности.
ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.
ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.
ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности.
ПК 1.3. Выполнять расчёты, необходимые при разработке технологических процессов изготовления отливок
ПК 3.3. Рассчитывать основные технико-экономические показатели работы коллектива,
осуществляется в части следующих результатов обучения.
Основные понятия, необходимые для выполнения ДКР
Теория пределов
Определение предела функции в точке
Сформулируем определение предела функции в точке.
Определение. Пусть функция f( x) определена в некоторой окрестности точки а, кроме, может быть, самой точки а, Число В называется пределом функции f( x) в точке а (или при х, стремящемся к а), если для любой последовательности значений аргумента хп ¹ а, п Î N, сходящейся к а, последовательность соответствующих значений функции f( xп), п Î N, сходится к числу В.
В этом случае пишут: 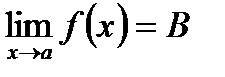 или
или 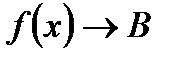 при
при 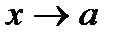 .
.
Если же для некоторой последовательности значений аргумента, сходящейся к а, соответствующая последовательность значений функции не является сходящейся, то функция в данной точке не имеет предела. То же заключение можно сделать, если для двух различных последовательностей значений аргумента последовательности соответствующих значений функции имеют различные пределы.
Очевидно, число В является пределом функции 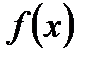 при
при 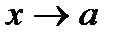 тогда и только тогда, когда
тогда и только тогда, когда 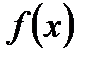 можно представить в виде:
можно представить в виде:
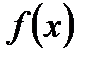 = В +
= В + 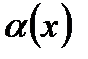 , где
, где 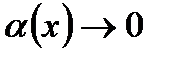 при
при 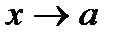 .
.
Отметим, что точка а, в которой рассматривается предел функции 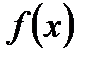 , может принадлежать области определения функции
, может принадлежать области определения функции 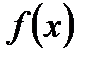 , а может и не принадлежать. При нахождении предела функции в точке не рассматривается значение функции в этой точке.
, а может и не принадлежать. При нахождении предела функции в точке не рассматривается значение функции в этой точке.
Свойства пределов функций
Основные свойства пределов функций аналогичны теоремам о пределах числовых последовательностей:
1) Предел суммы (разности) функций равен сумме (разности) их пределов, если последние существуют: 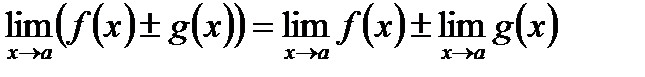 .
.
2) Предел произведения функций равен произведению их пределов, если последние существуют: 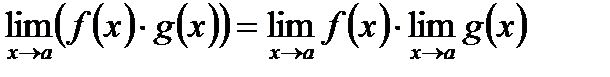 .
.
Следствие. Постоянный множитель можно выносить за знак предела: 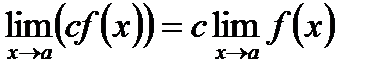 , если
, если 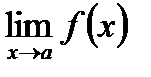 существует.
существует.
3) Предел отношения двух функций равен отношению их пределов, если последние существуют и предел делителя отличен от нуля: 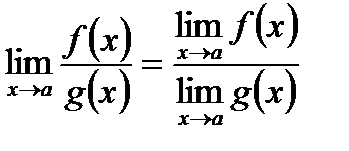 , если
, если 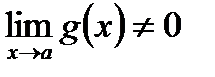 .
.
При изучении пределов функций иногда полезно использовать следующую «теорему о пределе промежуточной функции».
Теорема. Если 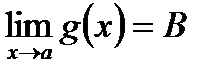 ,
, 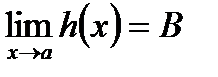 и в некоторой окрестности точки а, кроме, быть может, самой точки а, выполняются неравенства
и в некоторой окрестности точки а, кроме, быть может, самой точки а, выполняются неравенства 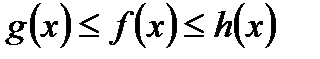 , то
, то 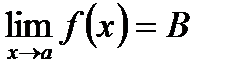 .
.
Дата: 2018-12-21, просмотров: 354.