В качестве определяющих особенностей олигополистического
рынка знаков следует указывать такие, как: ограниченное количество фирм, значительная концентрация производства у отдельных фирм, ограниченный доступ к отрасли, стратегическое поведение фирм.
В зависимости от производимого продукта различают однородные и дифференцированные олигополии. Однородные олигополии производят стандартизированный продукт. Многие промышленные продукты - сталь, цинк, медь, алюминий, свинец, цемент, технический спирт и т.д. - являются
стандартизированными продуктами в физическом смысле и производятся в условиях однородной олигополии. Но существуют и отрасли, где продукт является дифференцированным. Автомобили, станки, покрышки, моющие средства, сигареты, множество бытовых электрических изделий и т.д. - все это примеры дифференцированных олигополии. Независимо от этого, олигополистические рынки всегда характеризуются наличием значительной рыночной власти в фирмах и уменьшающейся кривой спроса на продукцию каждой отдельной фирмы. Однако их особенность заключается в том, что в условиях олигополистического взаимодействия (реакции на действия друг друга) фирмы сталкиваются не только с реакцией потребителей, но и с реакцией их конкурентов. Поэтому, в отличие от других рыночных структур, в случае олигополии фирма ограничена в принятии решений не только с наклоном кривой спроса, но и с действиями конкурентов.
В условиях олигополии конкурентное взаимодействие фирм влияет на все сферы конкуренции: цена, объем продаж, доля рынка, дифференциация продукции, стратегия продвижения товара, инновационная деятельность, услуги. В зависимости от ситуации, фирмы могут выбирать различные конкурентные стратегии. Поэтому для олигополистических рынков нет единой точки равновесия, к которой стремятся фирмы [13].
Поскольку нет общей модели олигополии, фирмы в одной отрасли могут взаимодействовать как монополии, так и конкурирующие фирмы. Все зависит от характера взаимодействия фирм. Когда отраслевые фирмы
координируют свои действия, имитируя стратегии ценообразования и конкуренции друг с другом (стратегия сотрудничества), цена и предложение будут иметь тенденцию монополизировать, и крайняя форма такой стратегии будет картелем. Если фирмы следуют несовместимой стратегии, т. е. проводят независимую стратегию, направленную на укрепление позиции фирмы, цены и предложение будут приближаться к конкурентным. Крайняя форма этого поведения - «ценовые войны» [9].
Модели олигополии
Модель Курно
Исторически первой является модель дуополии (олигополии при наличии на рынке двух фирм), которую в 1838 г. Предложил французский экономист Огюстен Курно.
Предпосылки рассматриваемой версии модели дуополии Курно сводятся к следующим допущениям:
1. На товарном рынке существуют только две фирмы-продавца, которые обслуживают множество покупателей.
2. Барьеры выхода на данный рынок являются непреодолимыми для других фирм-конкурентов.
3. Фирмы-дуополисты продают на рынке однородную продукцию.
4. Хозяйственное поведение фирм-продавцов является некооперированным (сговор между ними отсутствует).
5. Каждая из двух фирм, выбирая оптимальную величину выпуска, предполагает, что ее соперник сохранит объем реализации своей продукции на существующем уровне независимо от изменений ее собственного поведения на рынке .
6. В целях упрощения кривая общего рыночного спроса на продукцию двух фирм задана в виде линейной функции (формула 1).
P = P0 – kQ = P0 – k(q1+q2), (1)
где P- рыночная цена на продукцию двух фирм;
P0- резервная цена продукции, при которой потребительский спрос равен 0;
k- коэффициент чувствительности цены к динамике объема продаж, который показывает, на какую величину изменится цена продукции при изменении отраслевого объема продаж на единицу;
Q - отраслевой (суммарный) объем реализованной продукции двух фирм;
q1 и q2 - объемы продаж фирм 1 и 2.
7. Издержки производства у двух фирм одинаковые и заданы в виде следующих линейных функций:
TC1 = Cq1, и TC2 = Cq2 , (2)
где TC1 и TC2- величины общих издержек фирм 1 и 2;
C- величина предельных издержек каждой фирмы, равная средним издержкам.
В модели олигопольного рынка центральной предпосылкой является поведенческая характеристика фирм - их взаимозависимость. Поэтому, главным допущением модели Курно является то, что каждый дуополист рассматривает выпуск конкурента как заданную величину, которая не зависит от его собственных решений об объемах предложения своей продукции. И хотя это достаточно слабый вид взаимосвязи двух фирм, однако, даже он приводит в результате к тому, что хозяйственное поведение каждой фирмы серьезно влияет на действия ее конкурента [10].
Воспользовавшись графической моделью, проанализируем проблему выбора оптимально объема продаж для одной из фирм, например для фирмы 1. Прежде всего ей необходимо определить кривую спроса на свою продукцию. В соответствии с принятыми предпосылками фирма 1 считает, что объем выпуска фирмы 2 не зависит от принятого фирмой 1 решения и остается неизменным, в общем виде равным q2.
Тогда фирма 1 рассматривает в качестве кривой спроса на свою продукцию только ту часть кривой общего рыночного спроса, которая осталась ей от фирмы 2. С точки зрения фирмы 1, фирма 2 «захватила» первые q2 единиц продаж и соответствующую часть кривой рыночного спроса (D2, или отрезок P0A, на рис. 1), предоставив фирме 1 для работы оставшуюся часть этой кривой (D1, или отрезок AB, на рисунок 1). График D1 по этой причине часто называют кривой остаточного спроса.
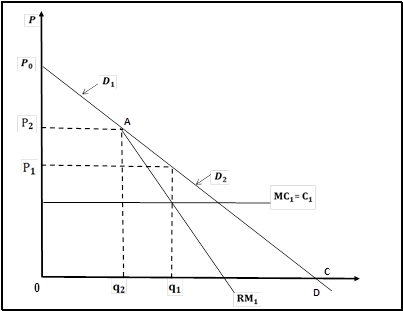
Рисунок 1 – Рыночный спроси и кривые спроса дуополистов
Величина продаж конкурента (q2) по предложению фирмы 1 фиксирована. Поэтому часть общей кривой рыночного спроса P0A является кривой спроса фирмы 2. Остаточная кривая спроса (D1) для фирмы 1 получается путем смещения вертикальной оси P вправо на величину объема продаж (q2) фирмы 2. Исходя из кривой остаточного спроса (D1) фирма 1 определяет график предельного дохода MR1.
Когда фирма 2 совсем ничего не продает (q2 = 0), фирма 1 может располагать всей кривой рыночного спроса (вся прямая линия D на рис. 1). Если величина продаж q2, больше 0, фирма 1 может графически построить свою кривую спроса (D1), сместив ось ординат (P) вправо на величину продаж (q2) конкурента.
На основе своей (остаточной) кривой спроса фирма 1 может определить соответствующий ей график предельного дохода MR1, который делит отрезок q2B ровно пополам. Графические построения фирмы 1 можно дополнить алгебраическим анализом. Функцию спроса на продукцию фирмы 1, которая (в момент принятия решения о величине собственных поставок на рынок) считает объем продаж конкурента фиксированным на уровне q2, можно записать в виде уравнения:
P1 = (P0 – kq2) – kq1, (3)
Общий доход первой фирмы в этом случае будет равняться:
TR1 = ( P0 – kq2)q1-kq12, (4)
Соответственно функция предельного дохода может быть представлена в виде:
MR1 =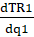 
= P0 – kq2 – 2kq1, (5)
Как и любая фирма на рынке несовершенной конкуренции, фирма-дуополист выбирает выпуск, исходя из принципа максимизации прибыли. А именно: фирма 1 продает столько своей продукции, чтобы было обеспечено равенство предельного дохода и предельных издержек.
Предельные издержки фирмы 1 в нашем случае равны:
MC1 =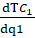 
= C, (6)
Поэтому выпуск фирмы 1, максимизирующий прибыль, является величиной, при которой предельный доход также равен С:
MR1 = MC1 P0 – kq2 – 2kq1 = C, (7)
Отсюда фирма 1 получает оптимальное решение:
q1 = 
- 
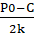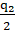, (8)
Полученное выражение, которое показывает, как объем продаж фирмы 1 будет реагировать на уровень поставок, предложенный фирмой 2, называют функцией реакции для фирмы 1, которую в общем виде представляют как q1 = r1(q2).
Проведя аналогичные рассуждения относительно выбора оптимального объема продаж вторым олигополистом, получим функцию реакции фирмы 2, которая имеет точно такой же вид:
q2 = -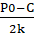 
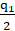, (9)
Таким образом, функция реакции - это кривая, которая показывает, какой объем продаж будет иметь один олигополист при каждом заданном объеме продукции, поставляемом на рынок другим олигополистом.
Как видно из полученных уравнений функции реакции фирм 1 и 2 графически представляют собой прямые линии (рис.2). Точка равновесия дуополистов находится в месте пересечения графиков их функций реакции (точка А на рис. 2). Координаты точки равновесия находятся из решения системы, включающей два уравнения, которые являются функциями реакции фирм 1 и 2:
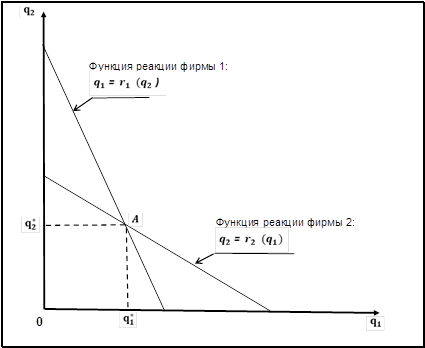
Рисунок 2 – Функции реакции дуополистов
Функция реакции каждого дуополиста определяет максимизирующую прибыль величину продаж как функцию объема продаж другой фирмы. Стабильное равновесие дуополистов возникает в точке пересечения их функций реакции.
 |
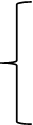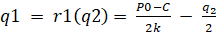функция реакции фирмы 1,
(10)
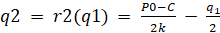функция реакции фирмы 2.
Уровни суммарного объема продаж двух дуополистов и цена их продукции в условиях равновесия по Курно располагаются между соответствующими параметрами равновесия на совершенно конкурентном рынке и рынке чистой монополии [9].
2.2 Ценовая война (Модель Бертрана)
Выводы, полученные из модели Курно, верны только в том случае, когда его предложения о характере взаимозависимости между фирмами-дуополистами являются справедливыми. Изменив эту предпосылку, другой французский экономист – Жозеф Бертран – в 1883 г. В порядке критики своего предшественника разработал альтернативную модель дуополии. Он оставил в силе все допущения модели Курно, изменив только одно из них, а именно: фирма, по Бертрану, выбирает не выпуск, а цену. При этом каждая фирма устанавливает свою цену, предполагая, что цена ее конкурента останется неизменной [11].
Допущение Бертрана приводит к результатам, весьма отличающимся от выводов его предшественника.
Пусть цена фирмы 1 равняется P1 (рис. 3). Тогда у фирмы 2 есть три варианта реагирования:
1. Назначить цену, равную цене продукции фирмы 1. В этом случае она поделит пополам с фирмой 1 существующие при этой цене объеме рыночного спроса и величину отраслевой прибыли.
2. Продавать свою продукцию по более низкой цене, чем фирма 1, и захватить весь рынок.
3. Назначить цену большую, чем у фирмы 1. Однако, в этом случае фирма 2 не сможет продать ничего, так как дуополисты реализуют однородный продукт и покупатели захотят покупать его у продавца с более низкой ценой.
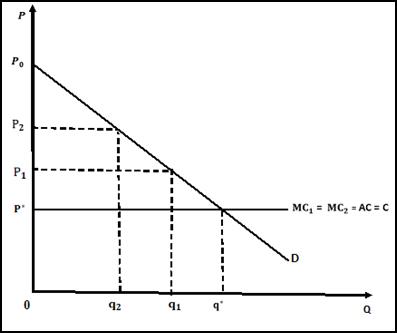
Рисунок 3 – Ценовая война в модели Бертрана
Последовательное уменьшение цены двумя фирмами будет продолжаться до тех пор, пока цена не сравняется со средними издержками и стимулы к её снижению не пропадут. Ценовая война, приводящая рыночные параметры к состоянию, характерному для рынка совершенной конкуренции, выгодна покупателям, но не выгодна продавцам [15].
Очевидно, второй вариант ценовой политики всегда принесёт фирме
наибольшую прибыль. Предположим, что второй продавец, не устояв перед соблазном, устанавливает свою цену P2 немного ниже, чем у фирмы 1, и, следовательно, заполучает весь рынок. При этом фирма 2 полагает (по Бертрану), что первый продавец не собирается отвечать ей тем же, и продажи фирмы 1 упадут до нуля. Однако теперь фирма 1 снижает цену. Она также полагает, как и её конкурент, цену соперника фиксированной и рассчитывает захватить весь рынок. В свою очередь фирма 2 отреагирует аналогично, продолжая снижать свои цены, и так далее. Цикл чередующихся снижений фирмами, конкурирующими на олигополистическом рынке, представляет собой ценовую войну.
Очевидно, что война цен будет продолжаться до тех пор, пока рыночная цена не упадет до уровня предельных (средних) издержек. В равновесии оба продавца назначают одну и ту же цену P* = AC = MC. Отраслевой объём продаж в результате будет таким же, какой имел бы место на рынке совершенной конкуренции.
Такой результат вполне закономерен. Мы убедились в том, что, предполагая неизменность текущей цены у конкурента, фирма всегда может увеличить прибыль, устанавливая цену немного ниже, чем её соперница. Однако, как и в дуополии Курно, положение двух фирм в модели Бертрана абсолютно симметрично. Это означает, что вариант продажи по цене ниже цены конкурента будет стратегией выбора для обеих фирм. Не может быть стабильного состояния равновесия, при котором одна из фирм продаёт продукцию по цене ниже уровня, установленного конкурентом. Поэтому вслед за одной фирмой другая фирма тут же снижает прежнюю цену. Ведь и она прекрасно понимает, что может получить большую прибыль, требуя с покупателя меньше цены, только что объявленной её конкурентом.
Ценовая война фирм будет продолжаться до тех пор, пока не будет достигнут естественный экономический предел, то есть величины предельных (средних) издержек. Дальнейшее снижение цены приведёт к отрицательной экономической прибыли, поэтому, когда каждая фирма снизит цену до величины предельных издержек, она не сможет больше уменьшать её в дальнейшем. При продаже каждой фирмой своей продукции по одной и той же цене, равной предельным издержкам, дуополисты поделят рынок поровну и будут получать нулевую экономическую прибыль [14].
Таким образом, нам пришлось убедиться в том, что кажущееся незначительным изменение только одной предпосылки о рыночном поведении фирмы – каждый дуополист рассматривает в качестве заданной величины цену своего конкурента, а не объём продаж – приводит к совершенно другому состоянию равновесия. В то время как в модели Курно равновесные цены и отраслевой объём продаж располагались в диапазоне между случаями совершенной конкуренции и чистой монополии, в модели Бертрана они точно такие же, как и в случае совершенно конкурентного рынка.
Модели дуополии Бертрана и Курно в первом приближении раскрывают суть и проблемы взаимозависимости при олигопольной структуре рынка. При этом две модели имеют один общий и существенный недостаток: обе построены на предпосылке, что решения, принимаемые фирмой, будут игнорироваться её конкурентами. И хозяйственная практика, и более ранние теоретические представления не соответствуют предположению обеих моделей относительно того, что фирма не берёт в расчёт возможное влияние собственных действий на рыночное поведение конкурента, как будто каждая фирма не понимает важности рыночной стратегии соперника. Поэтому дальнейшее развитие теории олигополии связано с преодолением этого недостатка моделей Курно и Бертрана [9].
2.3 Ассиметричная дуополия (модель Штакельберга)
Попытку преодолеть нереалистичность допущения моделей Курно и Бертрана в 1934 году предпринял немецкий экономист Генрих фон Штакельберг, который предположил, что дуополисты ведут себя на рынке асимметрично. Поэтому он выделил среди двух фирм на рынке фирму – лидера и фирму – последователя. Фирма - последователь ведёт себя на рынке строго по модели Курно. Следовательно, она игнорирует реакцию своего конкурента при принятии решения о собственном объёме поставок на рынке.
Исходя из этого, лидеру хорошо известно, что её единственный конкурент является «наивным» дуополистом Курно. По модели Штакельберга лидер постарается установить объём реализации своей продукции с учётом влияния, которое лидер окажет на уровень производства своего конкурента (последователя) [17].
Возвращаясь к нашему первому примеру, допусти что лидером является фирма 1. Теперь фирма 1 знает, что фирма 2 в своих расчётах будет считать уровень продаж фирмы 1 заданным. Следовательно, лидеру известна функция реакции фирмы 2, которая по модели Курно определяется уравнением:
q 2 = r 2 ( q 1 ) =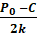 
− 
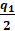, (11)
Для большей вероятности (и сопоставимости моделей Курно и Штакельберга) обозначим фирму-лидера символом L, фирму-последователя – p. Тогда функция реакции фирмы-последователя будет выглядеть следующим образом:
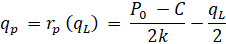, (12)
Таким образом, фирма 1 представляет уровень рыночных поставок фирмы 2 и будет зависеть от собственного объёма продаж, и сможет определить уравнение своей кривой спроса, подставив функцию реакции фирмы-соперника в уравнение отраслевого спроса:
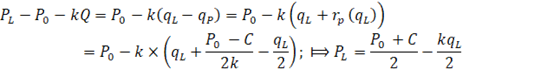(13)
На основе полученной функции полученной функции спроса фирма 1 может определить функцию своего предельного дохода:
MC =AC = C; M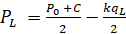 
, (14)
Поскольку предельные издержки и средние издержки равны C объём производства с максимальной прибылью фирмы 1, при условии MP = C, составит:
M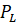 
= C ;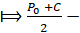 
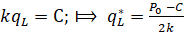, (15)
Кривая спроса фирмы 1 (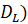 
и соответствующая ей кривая предельного дохода (M 
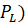показаны на рис. 4 а.
При таком объёме продаж рыночная цена продукции в модели дуополии Штакельберга будет выглядеть следующим образом:
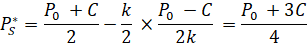, (16)
При этом, величина рыночных поставок лидера в дуополии Штакельберга совпадает с объёмом выпуска чистой монополии:
= 
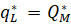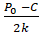, (17)
Заметим, что цены на этих рынках отличаются друг от друга. Для определения большей из них вычтем из цены на дуопольном рынке (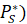 
цену чистой монополии (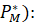 
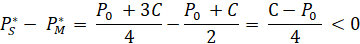, (18)
Таким образом, приходим к выводу, что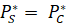 
.
Объём рыночных поставок фирмы – последователя в модели Штакельберга в 2 раза меньше, чем объём выпуска фирмы-лидера (и чистой монополии):
= 
= 
= 
= 
= 
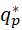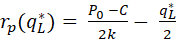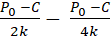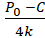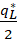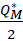, (19)
Для того чтобы определить как принимают решения фирма-лидер и фирма-последователь в модели Штакельберга, рассмотрим графическое изображение функций реакции двух фирм по Курно (рисунок 4 б). Оптимальным объёмом продаж для фирмы 1 (лидера) будет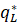 
, при этом фирма 2 (последователь) будет реагировать на выбор фирмы 1 в соответствии с положением в точке B на своей функции реакции. Таким образом, когда фирма 1 продаёт 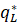, фирма 2 в соответствии со своей функцией ответит реализацией 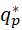единиц продукции [10].
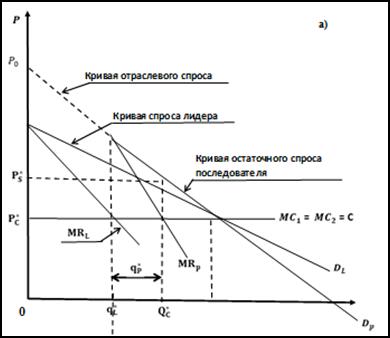
Рисунок 4а– Установление равновесия в модели Штакельберга
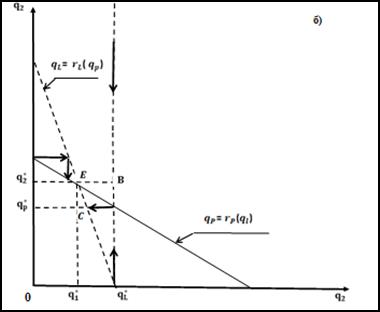
Рисунок 4б - Установление равновесия в модели Штакельберга
Разница между поведением фирмы 1 в моделях Курно и Штакельберга бесспорно. Если бы фирма 1 реагировала по Курно, то она считала бы, что фирма 2 остановится на уровне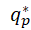 
. Тогда оптимальным вариантом поведения для неё было бы обращение к собственной функции реакции и решение продавать количество продукции, соответствующее точке C.
Фирма 1 (лидер) понимает, что если она сократит продажи до этой величины, то это повлечёт известную ей реакцию фирмы 2 и дальнейшее
движение конъюнктуры вплоть до точки А, точки пересечения двух функций реакции. Поэтому оптимальным решением для фирмы 1 будет оставаться на уровне .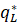
Если сопоставить хозяйственные результаты дуополистов Штакельберга, то, естественно, положение лидера предпочтительнее, чем последователя. Поскольку издержки и цены у фирм одинаковы, то прибыль фирмы-лидера, так же как и объём продаж в 2 раза больше прибыли фирмы – последователя.
Сравнивая общий объём продаж двух фирм, можно отметить, что в модели Штакельберга он выше, чем в модели Курно:
> 
= 
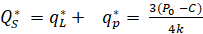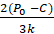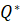, (20)
Напротив, рыночная цена здесь несколько ниже, чем в модели Курно:
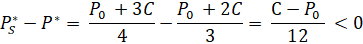, (21)
Как мы уже определили выше, рыночная цена при чистой монополии больше, чем в модели Штакельберга, а объём продаж у монополиста гораздо меньше:
< 
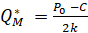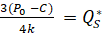, (22)
Таким образом, в модель Штакельберга цена выше, а выпуск меньше, чем при совершенной конкуренции:
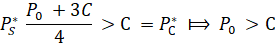, (23)
Отсюда следует, что дуополия по модели Штакельберга представлена более реалистичной, чем в моделях Курно и Бертрана, поскольку Штакельберг моделирует принятие стратегических решений для одной фирмы – лидера. Аналогичным образом может вести себя не только одна фирма
Использовать функцию реакции соперника в собственных стратегических интересах может не только фирма 1; фирма 2 со временем
будет действовать аналогично. А если обе фирмы попытаются одновременно стать лидерами, то каждая из фирм будет игнорировать собственную реакцию и продавать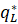 
объём продукции. В данном случае сложившиеся цена и отраслевой объём продаж будут такими же, как и в модели Бертрана.
У фирм появится интерес вступления в сговор. Разберём еще одну модель олигополии - модель Суизи [9].
Дата: 2018-12-21, просмотров: 292.
