Прежде чем приступить к разработке математической модели рассмотрим экономическую интерпретацию двойственной задачи.

Экономическую интерпретацию двойственной задачи рассмотрим на примере задачи оптимального использования ограниченных ресурсов. Для производства п видов продукции используется т видов ресурсов, запасы которых ограничены значениями b₁ ( 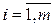 ). Норма расходов каждого ресурса на единицу продукции составляет а_ij  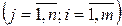. Цена единицы продукции j–го вида равняется с_j  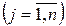. Математическая модель задачи имеет такой вид:

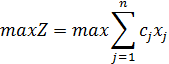
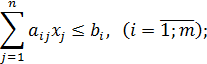
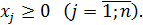
Прямая задача состоит в определении такого оптимального плана производства продукции X * = (х*₁, х*₂, ..., х*_п), который дает максимальный доход.

Двойственная задача по отношению к поставленной прямой имеет вид:

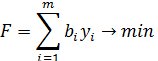
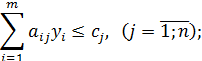
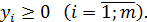
Экономическое содержание двойственной задачи состоит вот в чем. Определить такую оптимальную систему двойственных оценок ресурсов у_i, используемых для производства продукции, для которой общая стоимость всех ресурсов будет наименьшей. Поскольку переменные двойственной задачи означают ценность единицы і–го ресурса, их иногда еще называют теневой ценой соответствующего ресурса. С помощью двойственных оценок можно определить статус каждого ресурса прямой задачи и рентабельность изготавливаемой продукции.

Ресурсы, которые используются для производства продукции, можно условно разделить на дефицитные и недефицитные в зависимости от того, полное или частичное их использование предусмотрено оптимальным планом прямой задачи. Если двойственная оценка y_i, в оптимальном плане двойственной задачи равняется нулю, то соответствующий i–й ресурс используется в производстве продукции не полностью и является недефицитным. Если же двойственная оценка у_і > 0, то и ресурс используется для оптимального плана производства продукции полностью и называется дефицитным. В этом случае величина двойственной оценки показывает, на сколько увеличится значение целевой функции Z, если запас соответствующего ресурса увеличить на одну условную единицу.

Анализ рентабельности изготавливаемой продукции выполняется с помощью двойственных оценок и ограничений двойственной задачи. Левая часть каждого ограничения двойственной задачи является стоимостью всех ресурсов, которые используют для производства единицы j–ой продукции. Если эта величина превышает цену единицы продукции (с _j), изготовлять продукцию не выгодно, она нерентабельная и в оптимальном плане прямой задачи соответствующая х_j = 0. Если же общая оценка всех ресурсов равняется цене единицы продукции, то изготовлять такую продукцию целесообразно, она рентабельная и в оптимальном плане прямой задачи соответствующая переменная x_j > 0.

Экономическая интерпретация двойственных задач и анализ экономико–математических моделей на чувствительность с помощью теории двойственности дают возможность модифицировать оптимальный план задачи линейного программирования соответственно изменяющимся условиям прямой задачи и получить при этом такие результаты.

1. Изменение разных коэффициентов в прямой математической модели может повлиять на оптимальность и допустимость полученного плана и привести к одной из таких ситуаций:

• состав переменных и их значения в оптимальном плане не изменяются;

• состав переменных остается предыдущим, но их оптимальные значения изменяются;

• изменяются состав переменных и их значения в оптимальном плане задачи.

2.Включение дополнительного ограничения в математическую модель задачи влияет на допустимость решения и не может повлиять на улучшение значения целевой функции.

3.Включение новой переменной в математическую модель задачи влияет на оптимальность предыдущего плана и не ухудшает значения целевой функции.