Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Решение задач этой группы требует знаний учебного материала

темы 1 5, умения решать однофазные неразветвленные цепи, знать в трехфазных цепях соотношения между линейными и фазными напряжениями и токами при соединении потребителей «звездой» и «треугольником» и строить векторные диаграммы.

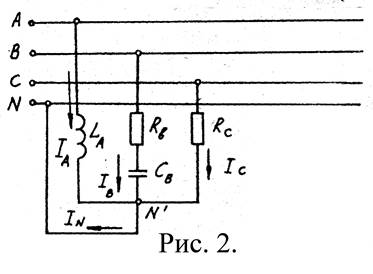
Пример 2. В трехфазную четырехпроводную сеть включили звездой несимметричную нагрузку: в фазу А - индуктивный элемент с индуктивностью L _A=31,8 мГн, в фазу В - резистор с сопротивлением R _B=30 Ом и ёмкостный элемент с ёмкостью C _B=795 мкф, в фазу C – резистор с сопротивлением R _С = 10 Ом. Линейное напряжение сети Uном=380В

Определить фазные токи I _A , I _B , I _C, активную мощность

цепи Р , реактивную мощность Q и полную мощность S, частота сети f=50Гц

Построить векторную диаграмму и по ней определить ток в нейтральном проводе.

Схема цепи дана на рис. 2.

 

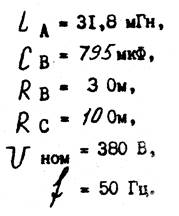Решение

Дано:

 

 

Определить: I _A, I _B, I _C, P, Q, S, I _N.

 

 

1. Определяем фазные напряжения:

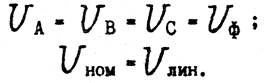
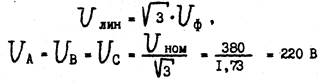В четырехпроводной цепи при любой нагрузке фаз выполняется соотношение:

 

 

2. Определяем сопротивление индуктивного элемента L _A:

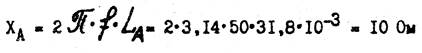
З. Определяем сопротивление емкостного элемента в фазе В:

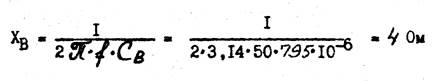
4. Определяем полное сопротивление в фазе В:

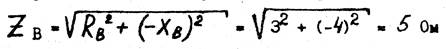
5. Находим фазные токи, применяя закон Ома для участка цепи:

6. Определяем активную мощность фазы А:

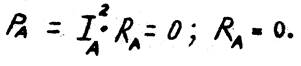
7. Определяем активную мощность фазы В:

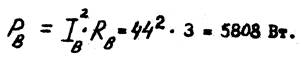
8. Определяем активную мощность фазы С:

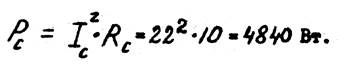
9. Активная мощность трехфазной цепи равна:

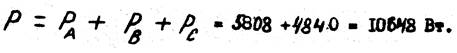
10. Определяем реактивную мощность фазы А:

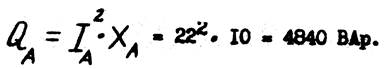
11. Определяем реактивную мощность фазы В:

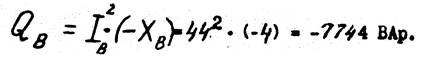
12. Определяем реактивную мощность фазы С:

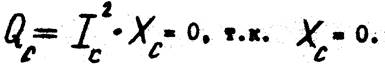
13. Реактивная мощность цепи:

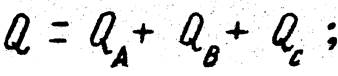
14. Полная мощность трехфазной цепи равна:

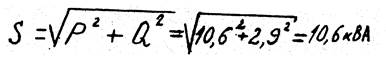
Для построения векторных диаграмм выбираем масштабы по току и напряжению:

Определяем длины векторов токов I _A , I _B , I _C и фазных напряжений U _A, U _B , U _C:

Определяем угол сдвига фаз меж током I _A и фазным напряжением U _A:

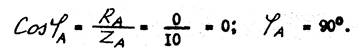
Вектор тока I _A отстаёт от напряжения на 90^o, так как в фазе А включен индуктивный элемент.

Определяем угол сдвига фаз между током I _B и напряжением U _B:

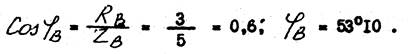
Вектор тока опережает напряжение на 53^о10 так как в фазе включена активно - емкостная нагрузка.

Определяем угол сдвига фаз между током I _C и напряжением U _C :

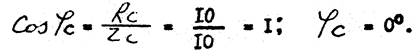
Вектор тока I _C совпадает по фазе с напряжением U_C, в фазе С включена активная нагрузка, на угол сдвига фаз равен

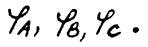Строим векторы фазных напряжений U _A , U _B , U_C под углом 120^о друг относительно друга и векторы фазных токов I _A , I _B , I _C, учитывая углы сдвига фаз

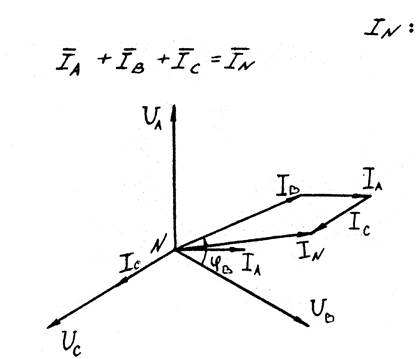На основании уравнения, составленного по 1-му закону Кирхгофа, строим вектор тока в нейтральном проводе

 

 

 

 

 Рис. 3

Измеряя длину вектора I_N получаем: l_IN = 4,4 см, отсюда I_N = l_IN *M_I =4,4*10=44А.

Ответ: I _A =22А, I _B =44А, I _C =22А, I _N =44А, Р=10,65 кВт, Q =2,9 кВАр, S = 10,6 кВА.

 

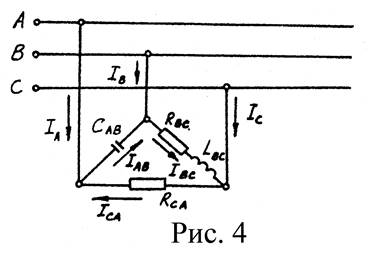
Пример 3. В трехфазную сеть включили треугольником несимметричную нагрузку. В фазу AB – емкостный элемент C_AB=318 мкф, в фазу BC – индуктивный элемент с активным сопротивлением R_BC = 4 Ом и индуктивностью L_BC = 9,6 мГн, в фазу CA – резистор с сопротивлением R_CA = 10 Ом. Линейное напряжение U_HOM = 220 В. Определить фазные токи, активную мощность P, реактивную мощность Q и полную мощность трехфазной цепи S. Частота цепи f = 50 Гц. Построить векторную диаграмму напряжений и токов и по ней определить линейные токи I_A , I_B , I_C . Схема цепи дана на рис. 4.

Решение

Дано:

 

Определить:

 

1. При соединении потребителей треугольником выполняется соотношение:

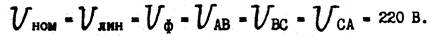
2. Определяем сопротивление емкостного элемента в фазе АВ:

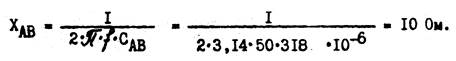
З. Определяем сопротивление индуктивного элемента в фазе ВС:

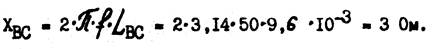
4. Определяем полное сопротивление фазы ВС:

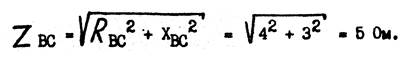
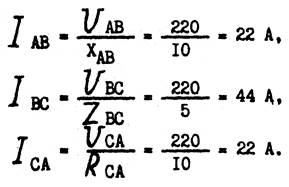
5. Определяем фазные токи:

6. Определяем активную мощность Р _АВ:

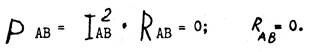
7. Определяем активную мощность Р _ВС :

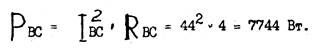
8. Определяем активную мощность фазы СА:

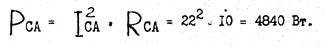
9. Определяем реактивную мощность фазы Q _АВ:

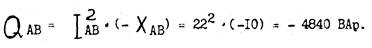
10. Определяем реактивную мощность Q _ВС :

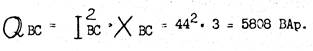
11. Определяем реактивную мощность Q _СА :

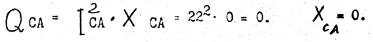
12. Определяем активную мощность трехфазной цепи:

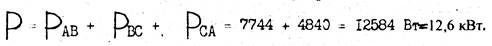
13. Определяем реактивную мощность всей цепи:

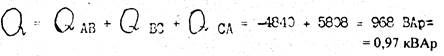
14. Определяем полную мощность трехфазной цепи:

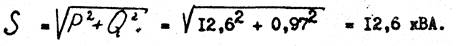
Для построения векторной диаграммы выбираем масштабы по току M_U = 10 А/см и по напряжению M_U = 50 В/см.

Определяем длины векторов фазных токов и фазных (они же линейные) напряжений:

Определяем угол сдвига фаз между током I _АВ и напряжением U_AB:

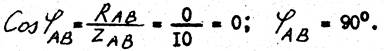
Вектор тока I _АВ опережает вектор напряжения U_A на 90^о так как а фазе АВ включен емкостный элемент.

Определяем угол сдвига фаз между током I _ВС и напряжением U_{B С} :

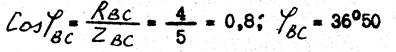
Вектор тока I _ВС отстает от вектора напряжения U_{B С} на угол 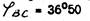, так как в фазе ВС включена активно - индуктивная нагрузка.

Определяем угол сдвига фаз между током I _СА и напряжением U _СА :

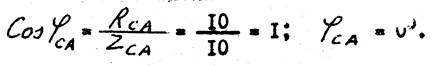
Вектор тока I _СА совпадает по фазе с вектором напряжения U _СА, так как нагрузка в фазе СА чисто активная,  

Строим векторы фазных напряжений U _АВ , U _ВС , U _СА под углом 120° друг относительно друга и векторы фазных токов I _АВ , I _ВС , I _СА с учётом углов сдвига фаз

Затем строим векторы линейных токов на основании уравнений, составленных по 1-му закону Кирхгофа.

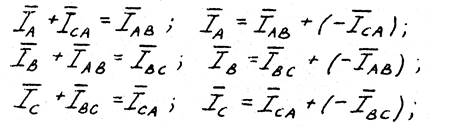
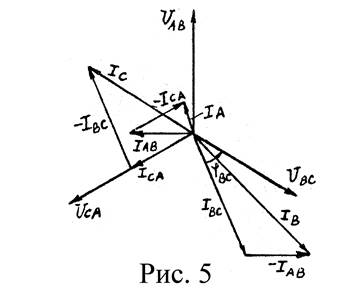
Измеряя длину векторов линейных токов I_A, I_B, I_C, получаем:

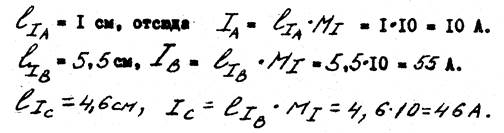
Ответ: I _АВ =22 А, I _{В C} =44 А, I_CA = 22 А, Р = 12,6 кВт, Q = 0,97 кВАр,

S= 12,64 кВА, I _А = 10 А, I_B= 55А, I_C =46 А.