Объемы геометрических тел.
Студент должен:
знать:
- понятия объема геометрического тела;
- формулы для вычисления объемов геометрических тел, перечисленных в содержании учебного материала;
уметь:
- находить объем прямой призмы, пирамиды, прямого кругового цилиндра и конуса, шара.
Объем геометрического тела. Объем призмы, пирамиды, цилиндра, конуса, шара.
Тема 10.2 Площади поверхностей
Студент должен:
знать:
- площади поверхности геометрического тела;
- формулы для вычисления площадей поверхностей геометрических тел, перечисленных в содержании учебного материала;
уметь:
- находить площади поверхностей призмы, пирамиды, цилиндра, конуса и шара.
Площадь поверхности геометрического тела. Площадь поверхности призмы, пирамиды, цилиндра, конуса и шара.
Контрольная работа №1
Примеры решения упражнений
1) Вычислить:
а) 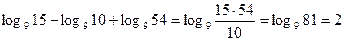
б) 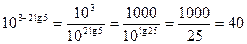
2) Решить уравнение:
а) 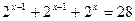 б)
б) 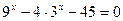
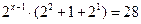
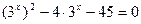
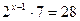
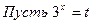
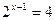
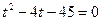
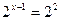

Функция y = 2t монотонна, значит 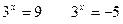
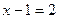
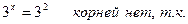
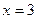

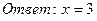
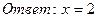
в) 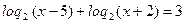
Область допустимых значений:
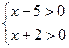
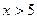
По свойству логарифма:
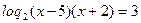
По определению логарифма:
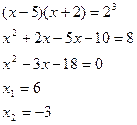
x 2 = -3 не удовлетворяет ОДЗ
Ответ. 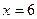
г) 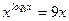
Область допустимых значений
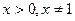
Прологарифмируем обе части уравнения по основанию 3:
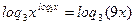
Применим свойства логарифма
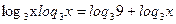
Пусть 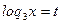
t2 = 2 + t
t2 – t – 2 = 0
t1 = 2 t2 = -1
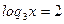
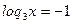
x1 = 32 x2 = 3-1
x1 = 9 x2 = 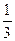
Ответ: x1 = 9, x2 = 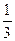 .
.
2) Решить неравенство:
а) 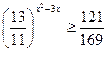
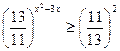
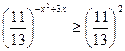
Т.к. 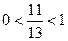 , то функция
, то функция 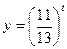 убывает:
убывает:
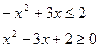

Решим неравенство методом интервалов:
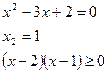
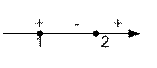
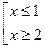
Ответ. 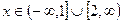

б)
|
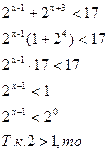

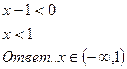
в) 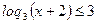

Область допустимых значений:
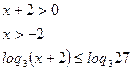
Т.к. 3>1, то функция y=loq3t возрастает:

Таким образом, исходное неравенство равносильно системе неравенств:
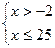
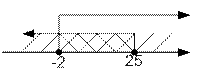
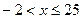
Ответ. 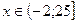
г) 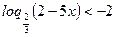
Область допустимых значений:
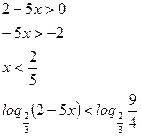
Т.к. 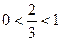 , то функция
, то функция 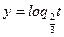 убывает:
убывает:
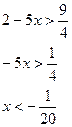
Таким образом, исходное неравенство равносильно системе неравенств:
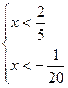
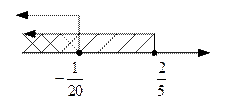
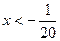
Ответ. 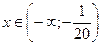
3.Вычислить 
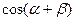 , если sin
, если sin 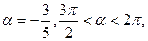 sin
sin 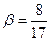 ,
, 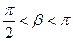
Дано:
sin 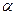 =
= 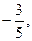
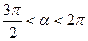

sin 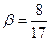 ,
, 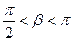
Найти: 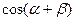
Решение: cos 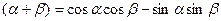 . Т.к.
. Т.к. 
4.Доказать тождество:а)
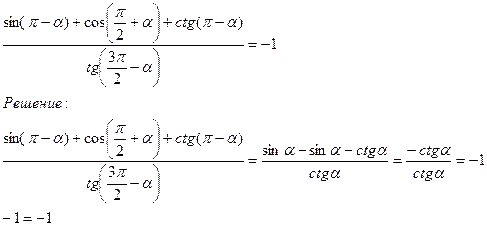
Что и требовалось доказать.
б)
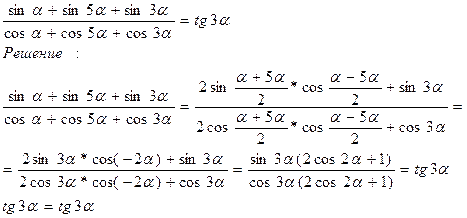
Что и требовалось доказать.
5.Решить уравнение:
a) 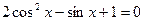
Решение:
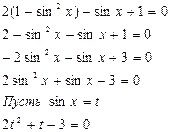
t 1 = - 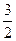
sin x = - 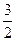
Корней нет, т.к. 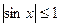
t 2 = 1
sin x = 1
x = 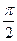 + 2
+ 2 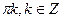
Ответ: x = 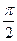 + 2
+ 2 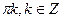
б) 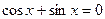
Решение:
Предположим, что cosx = 0. Тогда sinx = 0. Это противоречит основному тригонометрическому тождеству, т.к. 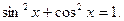 Значит,
Значит, 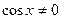
Разделим обе части исходного уравнения на cosx.
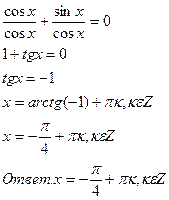
6.Решите задачу.
Прямоугольный треугольник с катетами 12см и 16см. Найдите расстояние от точки, до плоскости треугольника, если расстояния от этой точки до каждой вершины треугольника равны 26 см.
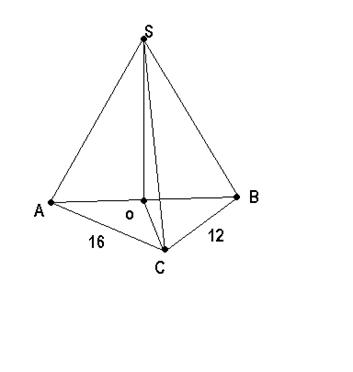
Дано:
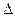 АВС-прямоугольный,
|AC|=16см, |BC|=12см.
|SA|=|SB|=|SC|=26см
Построение: АВС-прямоугольный,
|AC|=16см, |BC|=12см.
|SA|=|SB|=|SC|=26см
Построение:
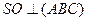 Т.к. |SA|=|SB|=|SC|, то
Т.к. |SA|=|SB|=|SC|, то  (по двум катетам). Значит, |AO|=|OB|=|OC|,
т.е О-центр описанной окружности около (по двум катетам). Значит, |AO|=|OB|=|OC|,
т.е О-центр описанной окружности около 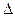 ABC, а т.к. ABC, а т.к. 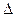 ABC-прямоугольный, то точка О-середина отрезка АВ.
Найти: |SO| ABC-прямоугольный, то точка О-середина отрезка АВ.
Найти: |SO|
|
Решение:
Рассмотрим 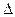 АВС. По теореме Пифагора |AB|=
АВС. По теореме Пифагора |AB|= 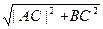
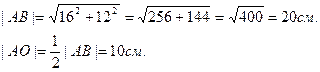
Рассмотрим 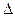 SOA-прямоугольный, т.к. SO
SOA-прямоугольный, т.к. SO 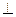 (ABC), по теореме Пифагора
(ABC), по теореме Пифагора
|SO|= 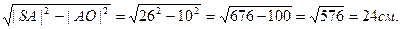
Ответ: |SO|=24 см.
Вариант 1
1) Вычислить:
а) 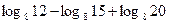
б) 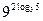
2) Решить уравнение:
а) 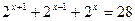
б) 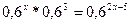
в) 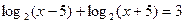
г) 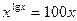
3) Решить неравенство:
а) 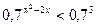
б) 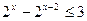
в) 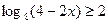
г) 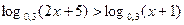
4.Вычислить sin( 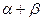 ), если sin
), если sin 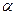 =-
=- 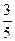 ,
, 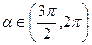 и sin
и sin 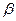 =
= 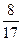 ,
, 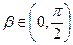 .
.
5.Доказать тождество:
a) 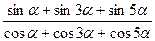 =tg3
=tg3 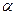 ;
;
b) 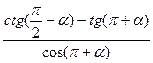 =0.
=0.
6.Решить уравнение:
a) 3cos2x – sin x – 1 =0;
b) cos x = sin x.
7.Катеты прямоугольного треугольника АВС равны 15 м и 20 м. Из вершины прямого угла С проведен к плоскости этого треугольника перпендикуляр CD=35 м. Найдите расстояние от точки D до гипотенузы АВ.
Вариант 2
1) Вычислить:
а) 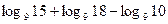
б) 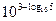
2) Решить уравнение:
а) 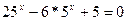
б) 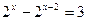
в) 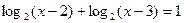
г) 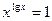
3) Решить неравенство: 
а) 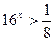
б) 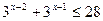
в) 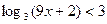
г) 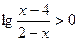
4.Вычислить cos( 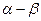 ), если cos
), если cos 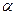 =
= 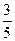 ,
, 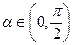 и cos
и cos 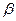 =-
=- 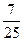 ,
, 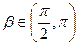 .
.
5.Доказать тождество:
a) 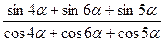 =tg5
=tg5 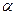 ;
;
b) cos( 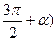 tg (
tg ( 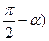 - sin (
- sin ( 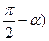 ) + ctg (
) + ctg ( 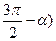 = tg
= tg 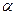
6.Решить уравнение:
a) 2 + cos2x – 2sin x =0;
b) sin2x – sin x cos x – 2 cos2 x = 0.
7.Стороны треугольника 10 см, 17 см и 21 см. Из вершины большего угла этого треугольника проведен перпендикуляр к его плоскости, равный 15 см. Определить расстояние от его концов до большей стороны.
Вариант 3
1) Вычислить:
а) 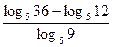
б) 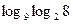
2) Решить уравнение:
а) 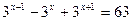
б) 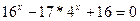
в) 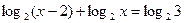
г) 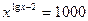
3) Решить неравенство: 
а) 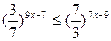
б) 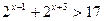
в) 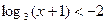
г) 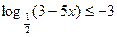
4.Вычислить sin( 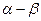 ), если sin
), если sin 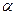 =-
=- 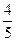 ,
, 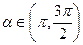 и cos
и cos 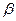 =-
=- 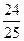 ,
, 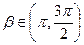 .
.
5.Доказать тождество:
a) 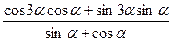 =cos
=cos 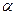 - sin
- sin 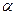 ;
;
b) 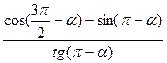 =2cos
=2cos 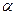 .
.
6.Решить уравнение:
a) sin2x – 3sin x cos x + 2 cos2 x = 0;
b) ccsx + cos3x = 4cos2x.
7.Из точки, отстоящей от плоскости на расстоянии 2 см, проведены две наклонные, образующие с плоскостью углы в 450, а между собой угол в 600. Найти расстояние между концами наклонных.
Вариант 4
1) Вычислить:
а) 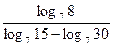
б) 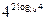
2) Решить уравнение:
а) 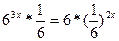
б) 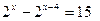
в) 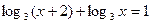
г) 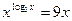
3) Решить неравенство:
а) 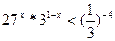
б) 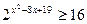
в) 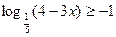
г) 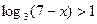
4.Вычислить cos 6300 – sin 14700 – ctg 11250.
5.Доказать тождество:
a) 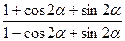 tg
tg  = 1;
= 1;
b) 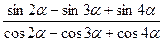 =tg3
=tg3  .
.
6.Решить уравнение:
c) 2sinx + sin2x = 0;
d) 3sin 2x - 5sinx -2 = 0.
7.Стороны треугольника равны 17, 15 и 8 см. Через вершину А меньшего угла треугольника проведена прямая АМ, перпендикулярная к его плоскости. Найти расстояние от точки М до прямой, содержащей меньшую сторону треугольника, если длина отрезка АМ равна 20 см.
Вариант 5
1) Вычислить:
а) 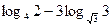
б) 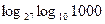
2) Решить уравнение:
а) 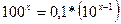
б) 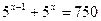
в) 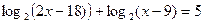
г) 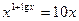
3) Решить неравенство:
а) 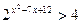
б) 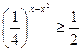
в) 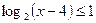
г) 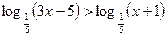
4.Вычислить sin2  , если cos
, если cos  =-
=- 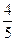 ,
, 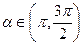 .
.
5.Доказать тождество:
a) 1 + cos 2  + 2 sin2
+ 2 sin2  = 2;
= 2;
b) 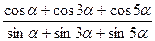 =ctg3
=ctg3  .
.
6.Решить уравнение:
a) 2sin2x + 3cos x = 0;
b) 2sin x + cos x = 0.
7.Из точки, отстоящей от плоскости на расстоянии 3 см, проведены две наклонные, образующие с плоскостью углы в 450 и 300, а между собой прямой угол. Найти расстояние между концами наклонных.
Вариант 6
1) Вычислить:
а) 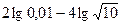
б) 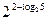
2) Решить уравнение:
а) 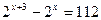
б) 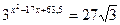
в) 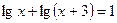
г) 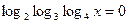
3) Решить неравенство:
а) 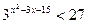
б) 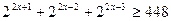
в) 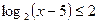
г) 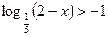
4.Вычислить sin(  +
+ 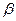 ), если cos
), если cos  =-
=- 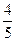 ,
, 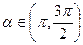 и sin
и sin 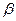 = -
= - 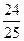 ,
, 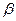
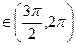 .
.
5.Доказать тождество:
a) 1 - cos( 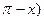 - sin(
- sin( 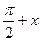 ) = 1;
) = 1;
b) sin( 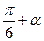 ) + sin(
) + sin( 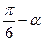 ) = cos
) = cos  .
.
6.Решить уравнение:
a) 1 + cosx + cos2x = 0;
b) sin2x + -3sin2x + 8cos2x = 0.
7.Из точки K, удаленной от плоскости  на 9 см, проведены к плоскости
на 9 см, проведены к плоскости  две наклонные KL и KM, образующие с плоскостью углы в 450 и 300 соответственно, а между собой прямой угол. Найти длину отрезка LM.
две наклонные KL и KM, образующие с плоскостью углы в 450 и 300 соответственно, а между собой прямой угол. Найти длину отрезка LM.
Вариант 7
1) Вычислить:
а) 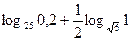
б) 
2) Решить уравнение:
а) 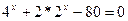
б) 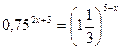
в) 
г) 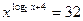
3) Решить неравенство:
а) 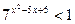
б) 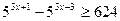
в) 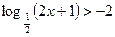
г) 
4.Вычислить cos( 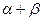 ), если sin
), если sin  =
= 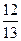 ,
, 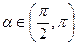 и sin
и sin 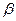 =-
=- 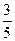 ,
, 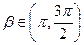 .
.
5.Доказать тождество:
a) 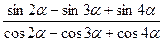 =tg3
=tg3  ;
;
b) tg(-  )ctg (
)ctg ( 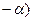 + cos2(
+ cos2( 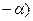 ) + sin2
) + sin2  = 2.
= 2.
6.Решить уравнениие:
a) cos( 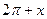 ) + 2sin(
) + 2sin( 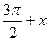 ) = 1;
) = 1;
b) 2sin x cos x – cos 5x sin2x = 0.
7.Из вершины прямого угла прямоугольного треугольника с катетами 15 см и 20 см проведен перпендикуляр длиной 16 см к плоскости треугольника. Найти расстояние от концов перпендикуляра до гипотенузы.
Вариант 8
1) Вычислить:
а) 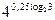
б) 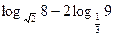
2) Решить уравнение:
а) 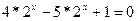
б) 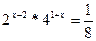
в) 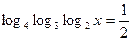
г) 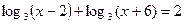
3) Решить неравенство:
а) 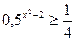
б) 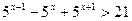
в) 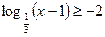
г) 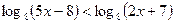
4.Вычислить tg5850 – cos10800 + cos15000.
5.Доказать тождество:
a) 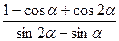 = ctg2
= ctg2  ;
;
b) 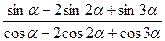 =tg2
=tg2  .
.
6.Решить уравнение:
a) cos 2x – sin2x – sin4xcos2x = 0;
b) sin(2700 - x) + sin(1800 - x) = 0.
7.Стороны треугольника равны 15, 37 и 44 см. Из вершины большего угла треугольника восстановлен к его плоскости перпендикуляр, равный 16 см. Найти расстояние от его концов до большей стороны.
Вариант 9
1) Вычислить:
а) 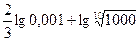
б) 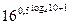
2) Решить уравнение:
а) 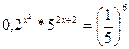
б) 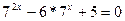
в) 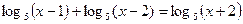
г) 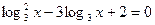
3) Решить неравенство:
а) 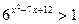
б) 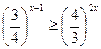
в) 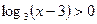
г) 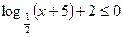
4.Вычислить cos8700 – sin12000 – 3tg5100.
5.Доказать тождество:
a) 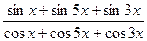 = tg3x;
= tg3x;
b) 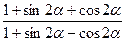 =ctg
=ctg  .
.
6.Решить уравнение:
a) cos5x + cos3x = cos4x;
b) sin2( 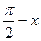 ) + sin(
) + sin( 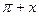 ) + 1 = 0.
) + 1 = 0.
7.Стороны треугольника равны 51, 30 и 27 см. Из вершины меньшего угла треугольника проведен к его плоскости перпендикуляр, равный 10 см. Найти расстояние от его концов до противоположной стороны треугольника.
Вариант 10
1) Вычислить:
а) 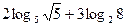
б) 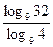
2) Решить уравнение:
а) 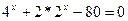
б) 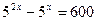
в) 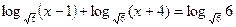
г) 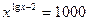
3) Решить неравенство:
а) 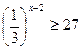
б) 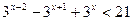
в) 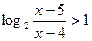
г) 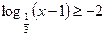
4.Вычислить cos( 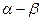 ), если sin
), если sin  =
= 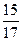 ,
, 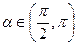 и cos
и cos 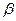 =-
=- 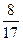 ,
, 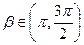 .
.
5.Доказать тождество:
a) 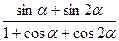 =tg
=tg  ;
;
b) 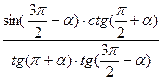 =sin
=sin  ;
;
6.Решить уравнениие:
a) 1 - cosx + sin 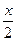 = 0;
= 0;
b) sin2x + sin2x = 3cos2x;
7.В треугольнике АВС длина отрезка АВ равна 13 см, длина отрезка ВС равна 14 см, длина отрезка АС равна 15 см. Из вершины А восстановлен к плоскости треугольника перпендикуляр AD, равный 5 см. Найти расстояние от точки D до стороны ВС.
Контрольная работа №2
Примеры решения упражнений
- Дана функция
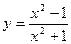 . Найдите
. Найдите 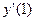 .
.
Решение:
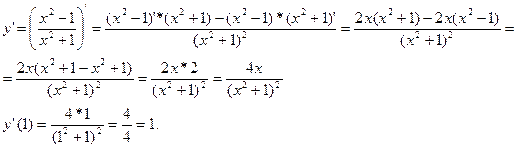
Ответ: 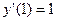
- Дана функция y=lncosx . Найдите
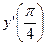
Решение:
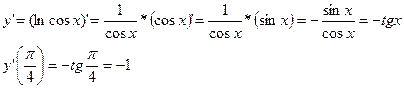
Ответ. 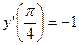
- Найдите экстремумы функции:
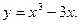
Решение:
Найдем производную функции:
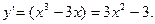
Найдем критические точки:
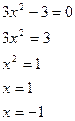
Исследуем знак производной на промежутках, на которые найденные критические точки делят область определения функции:





 + - + y/
+ - + y/
-1 1 y
x = -1 – точка максимума
x = 1 – точка минимума
Найдём значение функции 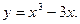 в найденных точках:
в найденных точках:
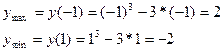
Ответ. max (-1,2), min (1,2)
- Постройте график функции:
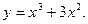
1) Найдем область определения функции:

2) Данная функция не является ни четной, ни нечетной, ни периодической.
3) Найдем область пересечения с осями координат:
С осью Ox:
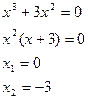
С осью Oy:
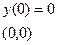
4) Найдем экстремумы функции:



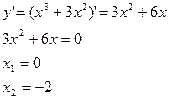
+ - + y/
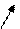

-2 0 y
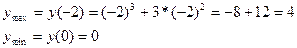
5) Найдём точки перегиба:

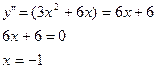 y
y

 - +
- +

 4
4
-1
 2 2
2 2




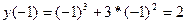
6) Построим график функции: -3-2-1 1
- В прямом параллелепипеде стороны основания равны
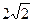 см и 5см и образуют угол в
см и 5см и образуют угол в 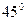 , меньшая диагональ параллелепипеда равна 7 см.
, меньшая диагональ параллелепипеда равна 7 см.
Найдите длину бокового ребра параллелепипеда.
B1 C1
 A1 D1
B C
A D
A1 D1
B C
A D
|
Дано:
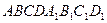 - прямой параллелепипед .
|AB|= - прямой параллелепипед .
|AB|= 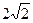 см., |AD|=5 см., см., |AD|=5 см., 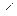 BAD= BAD= 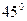 ; | ; | 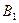 D|=7 см.
Найти. |B D|=7 см.
Найти. |B 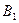 | |
|
Решение:
Рассмотрим треугольник ABD.
По теореме косинусов:
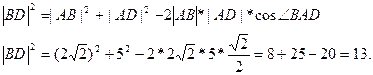
Рассмотрим треугольник 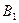 BD- прямоугольный;
BD- прямоугольный;
Т.к. параллелепипед прямой то по теореме Пифагора:
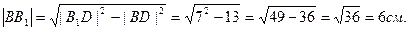
Ответ: | 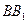 | = 6 см.
| = 6 см.
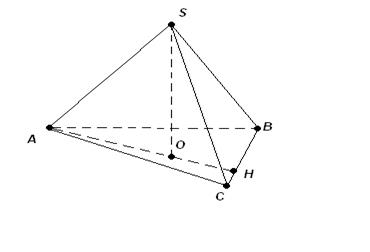
- Основанием пирамиды является треугольник со сторонами 39 см, 17 см, 28см, боковые рёбра равны каждое 22,9 см.
Найдите высоту пирамиды.
| Дано:
SABC-пирамида, |AB|=39 см, |BC|=17 cм, |AC|=28 см,
|SA|=|SB|=|SC|=22,9 см.
Построение:
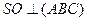 Т.к. |SA|=|SB|=|SC| то, О-центр описанной около
Т.к. |SA|=|SB|=|SC| то, О-центр описанной около 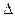 АВС окружности.
Найти |SO|. АВС окружности.
Найти |SO|.
|
Решение:
Рассмотрим 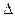 АВС. Найдём площадь этого треугольника по формуле Герона:
АВС. Найдём площадь этого треугольника по формуле Герона:
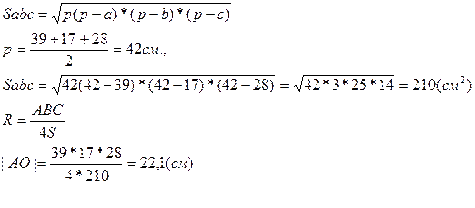
Рассмотрим  SOA-прямоугольный, т.к.
SOA-прямоугольный, т.к.  .
.
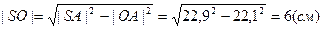
Ответ. |SO| = 6 см.
- Образующая конуса равна 6 см и наклонена к плоскости основания под углом 600. Найдите высоту конуса.
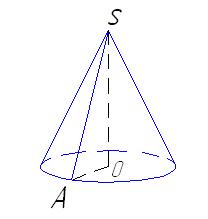
| Дано:
Конус, |SA|=6 см, 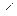 SAO= SAO= 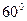 .
Найти |SO|. .
Найти |SO|.
|
Решение:
Рассмотрим 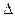 SOА - прямоугольный.
SOА - прямоугольный.
sin 60 0 = 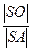
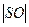 =
= 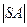 sin 60 0 = 6
sin 60 0 = 6 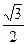 = 3
= 3 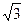 см.
см.
Ответ. |SO| = 3 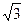 см.
см.
8.Найдите дифференциал функции y = etgx.
Решение:
dy = (etgx)/ dx = 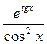 dx.
dx.
9.Найдите все первообразные функции:
а) y = 6sinx + 5
Решение:
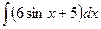 =
= 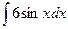 +
+ 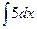 = -6cosx + 5x + C
= -6cosx + 5x + C
б) y = 2x4
Решение:
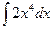 =
= 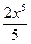 + C
+ C
в) y = 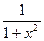 - 4x
- 4x
Решение:
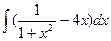 =
= 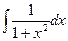 -
- 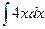 = arctg x -
= arctg x - 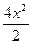 + C = arctg x – 2x2 + C
+ C = arctg x – 2x2 + C
10.Вычислите определенный интеграл:
а) 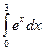
Решение:
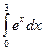 = ex
= ex 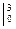 = e3 – e0 = e3 – 1
= e3 – e0 = e3 – 1
б) 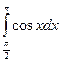
Решение:
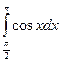 = sinx
= sinx 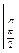 = sin
= sin 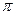 - sin
- sin 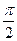 = 0 – 1 = -1
= 0 – 1 = -1
в) 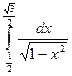
Решение:
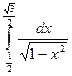 = arcsinx
= arcsinx 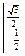 = arcsin
= arcsin 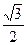 - arcsin
- arcsin 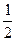 =
= 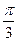 -
- 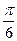 =
= 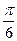
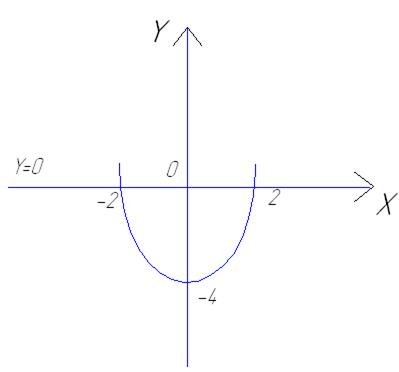
11.Найдите площадь фигуры, ограниченной линиями y = x2 – 4 и y = 0.
Дано:
y = x2 – 4
y = 0
Найти Sфигуры
Решение:
S = 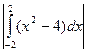 = = 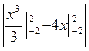 = = = = 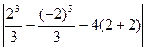 = = 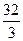 = =10 = =10 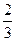 (кв.ед.)
Ответ. Площадь фигуры равна 10 (кв.ед.)
Ответ. Площадь фигуры равна 10  (кв.ед.) (кв.ед.)
| 
|
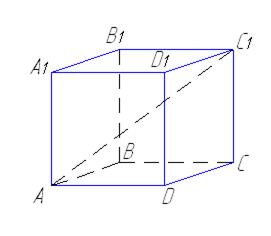
12.В прямом параллелепипеде стороны основания равны 1 м и 2 м и образуют угол в 600. Большая диагональ параллелепипеда равна 4 м. Найдите объем и боковую поверхность параллелепипеда.
 Решение:
V = Soh; Sбок = Роснh
So=
Решение:
V = Soh; Sбок = Роснh
So= 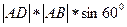 = 2 = 2  1 1  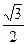 = = 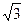 (м2)
По теореме косинусов: (м2)
По теореме косинусов: 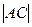 2 = 2 = 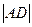 2 + 2 + 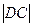 2 – 2 2 – 2  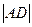  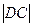  cos1200 = 22 + 12 – 2 cos1200 = 22 + 12 – 2  2 2  1 1  (- (- 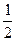 ) = 7 (м2)
Рассмотрим прямоугольный треугольник ACC1. По теореме Пифагора: ) = 7 (м2)
Рассмотрим прямоугольный треугольник ACC1. По теореме Пифагора: 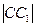 = = 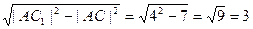 (м).
V = (м).
V = 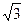  3 = 3 3 = 3 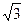 (м3).
Sбок = (2+1) (м3).
Sбок = (2+1)  2 2  3 = 18 (м2).
Ответ. V = 3 3 = 18 (м2).
Ответ. V = 3 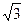 (м3), Sбок = 18 (м2). (м3), Sбок = 18 (м2).
| Дано:
ABCDA1B1C1D1 – прямой параллелепипед
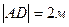 , , 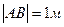 , , 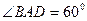 , , 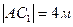 .
Найти: V, Sбок .
Найти: V, Sбок
|
13.Площадь основания конуса равна 16  дм2, а боковая поверхность 20
дм2, а боковая поверхность 20  дм2 . Найдите объем конуса.
дм2 . Найдите объем конуса.
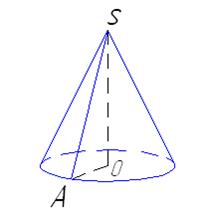 Дано: конус;
So = 16 Дано: конус;
So = 16  дм2, Sбок = 20 дм2, Sбок = 20  дм2.
Найти: V дм2.
Найти: V
|
Решение:
V = 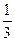 Soh;
Soh;
Так как в основании конуса лежит круг, то 
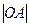 2 = 16
2 = 16  ;
;
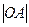 2 = 16;
2 = 16;
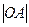 = 7 (дм).
= 7 (дм).
Sбок = 

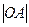

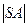 .
.
Подставим в формулу 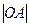 = 4, Sбок = 20
= 4, Sбок = 20 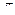 .
.

 4
4 
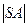 = 20
= 20  ;
;
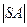 = 5 (дм).
= 5 (дм).
Рассмотрим прямоугольный треугольник SOA. По теореме Пифагора |SO|= 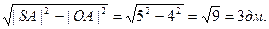
V = 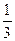
 16
16 
 3 = 16
3 = 16  (дм3).
(дм3).
Ответ. V = 16  (дм3).
(дм3).
Вариант 1
1. Дана функция y= 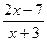 . Найдите y'(-2)
. Найдите y'(-2)
2. Дана функция y=ln sin x. Найдите y' (-π/4)
3. Найдите экстремумы функции: y = 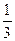 x3 – 2x2.
x3 – 2x2.
4. Постройте график функции: y =2x2 – 8x.
5. В прямом параллелепипеде стороны основания равны 3см и 5см и образуют угол в 60◦. Площадь большого диагонального сечения равна 63 см2. Найдите боковое ребро параллелепипеда.
6. Основанием пирамиды служит прямоугольный треугольник, катеты которого 15 см и 20 см, каждая боковая грань наклонена к основанию под углом 60◦. Найдите высоту пирамиды.
7. Площадь осевого сечения цилиндра равна 10 м2, а площадь основания - 4  м2. Найдите высоту цилиндра.
м2. Найдите высоту цилиндра.
8. Найдите дифференциал функции y = (1 – x2)5.
9. Найдите все первообразные функции:
a) y = 5sinx – 4 б) y = x2 в) y = 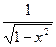 +x
+x
10. Вычислите определенный интеграл:
a) 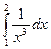 б)
б) 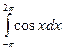 в)
в) 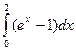
11. Найдите площадь фигуры, ограниченной линиями:
y = 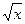 +1, y = 0, x = 0, x = 1.
+1, y = 0, x = 0, x = 1.
12. Основанием пирамиды служит прямоугольный треугольник, катеты которого 15 см и 20 см, каждая боковая грань наклонена к основанию под углом 45◦. Найдите площадь боковой поверхности и объем пирамиды.
13. Высота и образующая конуса относятся как 35:37. Полная поверхность конуса равна 588  см2. Найдите площадь боковой поверхности и объем конуса.
см2. Найдите площадь боковой поверхности и объем конуса.
Вариант 2
1. Дана функция y= 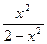 . Найдите y'(1)
. Найдите y'(1)
2. Дана функция y=ctg 4x. Найдите y' ( 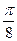 )
)
3. Найдите экстремумы функции: y =2x4 – x
4. Постройте график функции: y = - 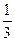 х3 + х2 - 6.
х3 + х2 - 6.
5. Стороны основания прямой треугольной призмы равны 3 см, 25 см и 26 см, а площадь большей боковой грани равна 260 см2. Найдите боковое ребро призмы.
6. Основание пирамиды – треугольник со сторонами, равными 6 см, 10 см и 14 см. каждый двугранный угол при основании равен 30◦. Найдите высоту пирамиды.
7. Высота конуса равна 15 см, а радиус основания равен 8 см. Найдите образующую конуса.
8. Найдите дифференциал функции y = ln sinx.
9. Найдите все первообразные функции:
a) y = cosx + 2 б) y = 4x3 в) y = 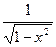 - x
- x
10. Вычислите определенный интеграл:
a) 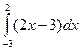 б)
б) 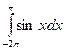 в)
в) 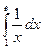
11. Найдите площадь фигуры, ограниченной линиями:
y = 4 – x2, y = 0.
12. В прямом параллелепипеде стороны основания равны 3 дм и 8 дм, угол между ними 600. Зная, что большая диагональ параллелепипеда равна 49 дм, найдите боковую поверхность и объем параллелепипеда.
13. Радиусы оснований усеченного конуса и его высота относятся как 3:6:4. Вычислите боковую поверхность и объем конуса, если его образующая равна 25 см.
Вариант 3
1. Дана функция y= 5х ∙ х5 . Найдите y'(0)
2. Дана функция y=еtgx . Найдите y' (0)
3. Найдите экстремумы функции: y = 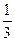 х3 – х2
х3 – х2
4. Постройте график функции: y =х3 - 6х + 16
5. Основание прямого параллелепипеда параллелограмм со сторонами 8 см и 32 см и острым углом 60◦. Большая диагональ параллелепипеда равна 40 см. Найдите высоту параллелепипеда.
6. Основание пирамиды – равнобедренный треугольник, у которого основание равно 6 см, а высота 9 см, боковые ребра равны между собой, и каждое содержит 13 см. Найдите высоту пирамиды.
7. Образующая конуса равна 12 см и наклонена к плоскости основания под углом 300. Найдите радиус основания конуса.
8. Найдите дифференциал функции y = ln cosx.
9. Найдите все первообразные функции:
a) y = 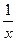 б) y = 6x4 в) y =
б) y = 6x4 в) y = 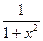 +2
+2
10. Вычислите определенный интеграл:
a) 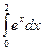 б)
б) 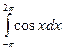 в)
в) 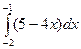
11. Найдите площадь фигуры, ограниченной линиями:
y = 9 – x2, y = 0.
12. Основанием пирамиды служит прямоугольный треугольник, катеты которого 15 см и 20 см, каждая боковая грань наклонена к основанию под углом 600. Найдите полную поверхность пирамиды и объем.
13. Высота усеченного конуса равна 3 см. Радиус одного основания вдвое больше радиуса другого, а образующая наклонена к основанию под углом 450. Найдите боковую поверхность и объем этого конуса.
Вариант 4
1. Дана функция y= 4х3 – 5х2 + 1. Найдите y'(1).
2. Дана функция y=е sinx. Найдите y' (0)
3. Найдите экстремумы функции: y =2х3– 9х2 + 12х – 8
4. Постройте график функции: y =3х3 - х
5. Стороны прямого параллелепипеда равны 5см и 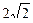 см, образуют угол 45◦ . Меньшая диагональ параллелепипеда равна 7см. Найдите боковое ребро параллелепипеда.
см, образуют угол 45◦ . Меньшая диагональ параллелепипеда равна 7см. Найдите боковое ребро параллелепипеда.
6. Основанием пирамиды служит равнобедренный треугольник, основание которого 12см и высота 18см. каждое из боковых ребер равно 26см. найдите высоту пирамиды.
7. Шар радиуса 41 дм пересечен плоскостью, находящейся на расстоянии 9 дм от центра. Найдите площадь сечения.
8. Найдите дифференциал функции y = sin 2 x.
9. Найдите все первообразные функции:
a) y = x3 б) y = 2 x - 1 в) y = 5sin x +2x
10. Вычислите определенный интеграл:
a) 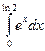 б)
б) 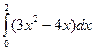 в)
в) 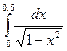
11. Найдите площадь фигуры, ограниченной линиями:
y = x2- 3, y = 0.
12. Основанием пирамиды служит треугольник со сторонами, равными 6 см, 10 см, 14 см. Каждый двугранный угол при основании равен 300. Найдите площадь боковой поверхности и объем этой пирамиды.
13. Боковая поверхность конуса 15 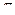 дм2, а полная поверхность 24
дм2, а полная поверхность 24 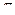 дм2. Найдите объем конуса.
дм2. Найдите объем конуса.
Вариант 5
1. Дана функция y= 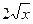 - 3. Найдите y'(1).
- 3. Найдите y'(1).
2. Дана функция y=5 sinx. Найдите y' (0).
3. Найдите экстремумы функции: y =2х3– 3х2 - 12х + 8
4. Постройте график функции: y = - х3 +3х
5. В прямой треугольной призме стороны основания равны 17см, 10см и 9см, а площадь меньшей боковой грани равна 90 см2. Найдите высоту призмы.
6. Основание пирамиды – прямоугольник со сторонами 6см и 8 см, каждое боковое ребро пирамиды равно 13 см. Найдите высоту пирамиды.
7. Найдите образующую усеченного конуса, если радиусы оснований равны 3 см и 6 см, а высота равна 4 см.
8. Найдите дифференциал функции y = cos 2 x.
9. Найдите все первообразные функции:
a) y = 5 x + e x б) y = x 5 в) y = 4 cos x – 3x2
10. Вычислите определенный интеграл:
a) 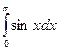 б)
б) 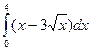 в)
в) 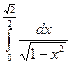
11. Найдите площадь фигуры, ограниченной линиями:
y = x2- 8, y = 0.
12. В основании пирамиды лежит равнобедренный треугольник, основание которого равно 12 дм, а боковая сторона 10 дм. Все боковые грани образуют с основанием углы 450. Найдите площадь боковой поверхности и объем пирамиды.
13. Образующая усеченного конуса равна 4 см и наклонена к плоскости основания под углом 600. Зная, что радиус большего основания равен 5 см, найдите боковую поверхность и объем усеченного конуса.
Вариант 6
1. Дана функция y = 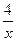 + 5х2. Найдите y'(1).
+ 5х2. Найдите y'(1).
2. Дана функция y = sin7х. Найдите y' (0).
3. Найдите экстремумы функции: y =2х3 + 9x2 + 12x
4. Постройте график функции: y = 9x - 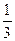 x3
x3
5. В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 300. Найдите высоту параллелепипеда.
6. Основанием пирамиды DABC служит треугольник со сторонами AB=AC=13см, BC=10см, ребро AD перпендикулярно к плоскости основания и равно 9 см. Найдите высоту грани DBC.
7. Угол между образующей и осью конуса равен 450, образующая равна 6,5 см. Найдите радиус основания конуса.
8. Найдите дифференциал функции y = arcsin x2.
9. Найдите все первообразные функции:
a) y = 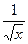 б) y = 2sinx + 1 в) y = 3x + cos x
б) y = 2sinx + 1 в) y = 3x + cos x
10. Вычислите определенный интеграл:
a) 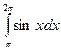 б)
б) 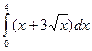 в)
в) 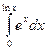
11. Найдите площадь фигуры, ограниченной линиями:
y = x2 + 1, y = 0, x = -1, x = 2.
12. Основание пирамиды – равнобедренный треугольник, у которого основание равно 6 см, а высота 9 см, боковые ребра равны между собой и каждое содержит 13 см. Найдите объем пирамиды.
13. Высота усеченного конуса равна 3 см. Радиус одного основания вдвое больше другого, а образующая наклонена к основанию под углом 450. Найдите площадь боковой поверхности и объем этого конуса.
Вариант 7
1. Дана функция y=3х3 – 4х +1. Найдите y'(1).
2. Дана функция y = ln5х. Найдите y' (-2).
3. Найдите экстремумы функции: y = 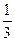 х3 - 4х
х3 - 4х
4. Постройте график функции: y = -0,5х2 + х + 1,5
5. Основанием прямоугольного параллелепипеда является параллелограмм со сторонами 3дм и 8дм, угол между ними 60◦. Найдите боковое ребро параллелепипеда, если большая диагональ параллелепипеда 49 дм.
6. Основанием пирамиды служит равнобедренный треугольник, у которого основание равно 12см, а боковая сторона 10 см. Боковые грани образуют с основанием равные углы по 45◦ . Найдите высоту пирамиды.
7. Радиусы оснований усеченного конуса равны 5 см и 11 см, образующая равна 10 см. Найдите высоту усеченного конуса.
8. Найдите дифференциал функции y = arccos 2x.
9. Найдите все первообразные функции:
a) y = 3cosx – 4sinx б) y = 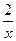 в) y =
в) y = 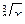
10. Вычислите определенный интеграл:
a) 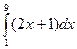 б)
б) 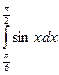 в)
в) 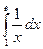
11. Найдите площадь фигуры, ограниченной линиями:
y = x3, y = 0, x = -1, x = 2.
12. Стороны прямого параллелепипеда равны 5 см и 2 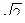 см, образуют угол 450, меньшая диагональ параллелепипеда равна 7 см. Найдите площадь полной поверхности и объем параллелепипеда.
см, образуют угол 450, меньшая диагональ параллелепипеда равна 7 см. Найдите площадь полной поверхности и объем параллелепипеда.
13. Площадь основания конуса 9 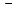 см2 , полная поверхность его 24
см2 , полная поверхность его 24 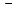 см2 . Найдите объем конуса.
см2 . Найдите объем конуса.
Вариант 8
1. Дана функция y=(3х2 – 2) (2 + 3х2). Найдите y'(-1).
2. Дана функция y = tg3х. Найдите y' (0).
3. Найдите экстремумы функции: y = - х3 + 2х2 – 8x + 1
4. Постройте график функции: y = 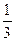 х3 - 9х
х3 - 9х
5. В прямоугольном параллелепипеде стороны основания равны 3см и 4см. Диагональ параллелепипеда образует с плоскостью основания угол в 45◦ . Найдите высоту параллелепипеда.
6. В основании пирамиды лежит прямоугольный треугольник с катетами 12см и 16см. Длина каждого бокового ребра равна 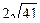 см. Найдите высоту пирамиды.
см. Найдите высоту пирамиды.
7. Образующая конуса, равная 10 см, наклонена к плоскости основания под углом 300. Найдите радиус основания конуса.
8. Найдите дифференциал функции y = e sinx.
9. Найдите все первообразные функции:
a) y = 2x – x2 б) y = 4sinx + 3 в) y = 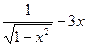
10. Вычислите определенный интеграл:
a) 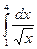 б)
б) 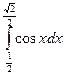 в)
в) 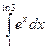
11. Найдите площадь фигуры, ограниченной линиями:
y = x3, y = 0, x = -2, x = 1.
12. Основание пирамиды – прямоугольник со сторонами 6 см и 8 см, каждое боковое ребро пирамиды равно 13 см. Найдите объем пирамиды.
13. Высота цилиндра на 10 см больше радиуса его основания, площадь полной поверхности равна 264 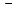 см2. Найдите площадь боковой поверхности и объем цилиндра.
см2. Найдите площадь боковой поверхности и объем цилиндра.
Вариант 9
1. Дана функция y= 5x + x5. Найдите y'(1).
2. Дана функция y = sin3х. Найдите y' (0).
3. Найдите экстремумы функции: y = -х4 + 4х - 4.
4. Постройте график функции: y = 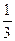 х3 - 2х2.
х3 - 2х2.
5. В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 450. Найдите боковое ребро параллелепипеда.
6. Боковое ребро и апофема правильной треугольной пирамиды соответственно равны 10 см и 6 см. Найдите стороны основания этой пирамиды.
7. Образующая конуса наклонена к плоскости основания под углом 300. Найдите образующую, если радиус основания конуса равен 6 см..
8. Найдите дифференциал функции y = e cosx.
9. Найдите все первообразные функции:
a) y = x3 + 3 б) y = 2sinx – 4x в) y = 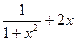
10. Вычислите определенный интеграл:
a) 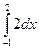 б)
б) 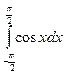 в)
в) 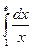
11. Найдите площадь фигуры, ограниченной линиями:
y = x2 – 4x + 3, y = 0.
12. В правильной четырехугольной усеченной пирамиде стороны оснований 16 м и 4 м. Найдите площадь полной поверхности и объем, если высота пирамиды равна 8 м.
13. Радиусы оснований усеченного конуса 6 м и 2 м, образующая наклонена к основанию под углом 450. Найдите площадь боковой поверхности и объем конуса.
Вариант 10
1. Дана функция y= 2 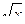 - x4. Найдите y'(1).
- x4. Найдите y'(1).
2. Дана функция y = cos2х. Найдите y' (0).
3. Найдите экстремумы функции: y = 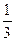 x3 -
x3 - 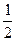 х2 + 6.
х2 + 6.
4. Постройте график функции: y = х3 - 3х.
5. Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 1200 между ними. Наибольшая из площадей боковых граней равна 35 см2. Найдите высоту призмы.
6. Основанием пирамиды является треугольник со сторонами 10 см, 10 см и 12 см. Каждая боковая грань наклонена к основанию под углом 450. Найдите высоту пирамиды.
7. Шар пересекает плоскость на расстоянии 9 см от центра, площадь сечения 1600  см2. Найдите радиус шара.
см2. Найдите радиус шара.
8. Найдите дифференциал функции y = 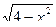
9. Найдите все первообразные функции:
a) y = 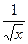 б) y = 3x2 + 1 в) y = 2x -
б) y = 3x2 + 1 в) y = 2x - 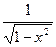
10. Вычислите определенный интеграл:
a) 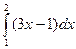 б)
б) 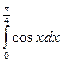 в)
в) 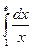
11. Найдите площадь фигуры, ограниченной линиями:
y = x2 + x - 6, y = 0.
12. В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 300. Найдите площадь полной поверхности и объем параллелепипеда.
13. Поверхность шара равна 225  м2. Определите его объем.
м2. Определите его объем.
Литература
Основные источники:
1. Атанасян Л.С. Геометрия (10-11 класс) - учебник для
общеобразовательных учреждений. Просвещение. 2008 г.
2. Богомолов Н.Б. Практические занятия по математике: учебное пособие
для студентов средних специальных учебных заведений.
Высш. шк., 2007г.
3. Богомолов Н.Б., П.И.Самойленко Математика: учебник для студентов
образовательных учреждений среднего профессионального образования.
Дрофа, 2006г.
4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в
упражнениях и задачах (в двух частях), 2006г.
5. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие для
студентов образовательных учреждений среднего профессионального
образования. – Ростов н/Д: Феникс, 2007г.
Дополнительные источники:
1. Григорьев В.П., Ю.А.Дубинский Элементы высшей математики:
учебник для студентов образовательных учреждений среднего
профессионального образования. Издательский центр «Академия»,
2004г.
2. Саакян С.М., А.М.Гольдман, Д.В.Денисов Задачи по алгебре и началам
анализа: пособие для учащихся 10 – 11 кл. Просвещение, 2005г.
3. Шипачев С.М. Начала высшей математики: пособие для вузов. Дрофа,
2002г.
Интернет-ресурсы:
1. http://en.edu/ru – естественнонаучный портал;
2. http://schools.techno.ru – сайт «Школы в Интернете»
3. http://www.school.edu.ru – российский образовательный портал
4. http://www.alleng.ru- сайт «Образовательные ресурсы Интернета
школьникам и студентам»
Дата: 2018-12-21, просмотров: 614.
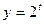 возрастает:
возрастает: