Нижнетагильский машиностроительный техникум
УТВЕРЖДАЮ
И.о. директора техникума
____________ Е.В. Гильдерман
« ___»_____________201 г.
Методические рекомендации
по выполнению домашней контрольной работы
для студентов заочной формы обучения
по дисциплине
«МАТЕМАТИКА»
основной образовательной программы
среднего (полного) общего образования
технический профиль,
базовый уровень
Нижний Тагил,
2017
Методические рекомендации разработаны в соответствии с рабочей программой учебной дисциплины «Математика», разработанной на основе Федерального государственного образовательного стандарта среднего (полного) общего образования, утвержденного приказом Министерства образования и науки Российской Федерации от 17 мая 2012 года № 413 и примерной программой, рекомендованной ФГАУ «ФИРО» для реализации основной профессиональной образовательной программы СПО протокол № 3 от 21.07.2015г.
| Организация разработчик: | ФГАОУ ВО «Уральский федеральный университет имени первого Президента России Б.Н. Ельцина» Нижнетагильский технологический и институт Нижнетагильский машиностроительный техникум |
| Разработчик: | преподаватель НТМТ Ведерникова Е.В. |
Методические рекомендации обсуждены и одобрены на заседании цикловой комиссии общеобразовательного, социально-экономического, математического и естественнонаучного цикла
| Протокол № ____ «___» _______ 201 г. | Председатель ЦК Ведерникова Е.В. |
Содержание
Введение
1. Пояснительная записка
1.1 Результаты освоения дисциплины
1.2 Основные понятия, необходимые для выполнения ДКР
1.3 Примеры решения задач
2. Задания для домашней контрольной работы
3. Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы.
Пояснительная записка
1.1 Результаты освоения дисциплины «Математика».
Тематический план и содержание учебной дисциплины соответствует рабочей программе учебной дисциплины «Математика» и обеспечивает достижение студентами следующих результатов:
• личностных:
−− сформированность представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, идеях и методах математики;
−− понимание значимости математики для научно-технического прогресса, сформированность отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей;
−− развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования;
−− овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для освоения смежных естественно-научных дисциплин и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки;
−− готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;
−− готовность и способность к самостоятельной творческой и ответственной деятельности;
−− готовность к коллективной работе, сотрудничеству со сверстниками в образовательной, общественно полезной, учебно-исследовательской, проектной и других видах деятельности;
−− отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем;
• метапредметных:
−− умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные стратегии в различных ситуациях;
−− умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты;
−− владение навыками познавательной, учебно-исследовательской и проектной деятельности, навыками разрешения проблем; способность и готовность к самостоятельному поиску методов решения практических задач, применению различных методов познания;
−− готовность и способность к самостоятельной информационно-познавательной деятельности, включая умение ориентироваться в различных источниках информации, критически оценивать и интерпретировать информацию, получаемую из различных источников;
−− владение языковыми средствами: умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;
−− владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств для их достижения;
−− целеустремленность в поисках и принятии решений, сообразительность и интуиция, развитость пространственных представлений; способность воспринимать красоту и гармонию мира;
• предметных:
−− сформированность представлений о математике как части мировой культуры и месте математики в современной цивилизации, способах описания явлений реального мира на математическом языке;
−− сформированность представлений о математических понятиях как важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;
−− владение методами доказательств и алгоритмов решения, умение их применять, проводить доказательные рассуждения в ходе решения задач;
−− владение стандартными приемами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств;
−− сформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей;
−− владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать геометрические фигуры на чертежах, моделях и в реальном мире; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием;
−− сформированность представлений о процессах и явлениях, имеющих вероятностный характер, статистических закономерностях в реальном мире, основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин;
−− владение навыками использования готовых компьютерных программ при решении задач.
Методические рекомендации
Работа студента над курсом математики на заочном отделении НТМТ предполагает самостоятельное изучение теоретического материала и выполнение значительного числа задач и упражнений, позволяющих глубже понять содержание курса и выработать необходимые навыки в выполнении стандартных математических операций. Этой цели служит контрольная работа, которую студент должен выполнить в течение семестра.
В данном методическом руководстве содержатся методические указания, необходимые для выполнения работы, а также варианты заданий для выполнения работы. Вариант контрольной работы студент выбирает по последней цифре номера студенческого билета.
При выполнении контрольной работы и представлении ее на проверку студент должен руководствоваться следующими правилами.
1. Каждая контрольная работа должна быть выполнена в отдельной тетради и сдана на проверку на заочное отделение в срок, установленный в индивидуальном графике студента.
2. Если при проверке контрольной работы обнаружены ошибки, то студент должен выполнить работу над ошибками и сдать ее для повторной проверки.
3. Решение задач из контрольной работы должно быть достаточно подробным и логически последовательным. Полезно в тексте решения приводить формулировки теорем и других теоретических сведений, на основании которых делаются Ваши заключения.
Студент – заочник должен иметь в виду, что вдумчивая самостоятельная работа над контрольными заданиями является залогом успешной сдачи зачета по математике.
1 ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Действительные числа. Приближенные вычисления и вычислительные средства.
Студент должен:
знать:
- определение действительного числа, абсолютной и относительной погрешности приближений;
- практические приемы вычислений с приближенными данными;
уметь:
- выполнять с заданной точностью на инженерном или программируемом (в режиме вычислений) микрокалькуляторе арифметические действия;
- вычислять значения элементарных функций.
Действительные числа. Приближение действительных чисел конечными десятичными дробями.
Погрешности приближений и вычислений. Практические приемы вычислений с приближенными данными.
Вычисления с помощью микрокалькуляторов. Вычисление значений выражений.
Определители.
Студент должен:
знать:
- понятия определителей второго и третьего порядка;
- способы решения систем линейных уравнений с двумя и тремя неизвестными;
уметь:
- вычислять определители второго и третьего порядка;
- решать системы линейных уравнений с двумя и тремя неизвестными с помощью определителей второго и третьего порядка.
Определители второго и третьего порядка. Решение систем линейных уравнений с двумя и тремя неизвестными с помощью определителей второго и третьего порядка, методом Крамера.
Предел функции.
Студент должен:
знать:
- определение предела функции в точке;
- свойства предела функции в точке;
- формулы замечательных пределов;
- определение непрерывности функции в точке,
- свойства непрерывных функций;
уметь:
- вычислять пределы функций в точке и на бесконечности.
Предел функции в точке. Основные свойства предела. Предел функции в точке и на бесконечности. Предел числовой последовательности. Первый и второй замечательные пределы. Непрерывность функции в точке и на промежутке. Свойства непрерывных функций.
Степень и ее свойства.
Студент должен:
знать:
- понятие степени с действительным показателем и ее свойства;
уметь:
- выполнять действия над степенями.
Степень с произвольным действительным показателем и ее свойства.
Логарифмы и их свойства.
Студент должен:
знать:
- определение логарифма числа;
- свойства логарифмов;
уметь:
- вычислять значения логарифмических выражений с помощью основных тождеств и вычислительных средств.
Логарифмы и их свойства. Натуральные логарифмы. Десятичные логарифмы. Преобразование и вычисление значений логарифмических выражений.
Показательная, логарифмическая и степенная функции, их свойства и графики.
Студент должен:
знать:
- свойства и графики показательной, логарифмической и степенной функций;
уметь:
- строить графики показательных, логарифмических функций при различных основаниях и на них иллюстрировать свойства функций; преобразовывать эти графики путем сдвига и деформации.
Показательная, логарифмическая, степенная функции, их свойства и графики. Построение показательных логарифмических и степенных графиков функций.
Показательные и логарифмические уравнения и неравенства.
Студент должен:
знать:
- способы решения простейших показательных и логарифмических уравнений;
- способы решения показательных и логарифмических неравенств;
уметь:
- решать несложные уравнения, приводимые к видам;
- решать несложные неравенства, приводимые к видам:
Показательные и логарифмические уравнения. Способы решения простейших и сводящихся к ним показательных и логарифмических уравнении, Показательные и логарифмические неравенства. Решение простейших показательных и логарифмических неравенств.
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Тождественные преобразования.
Студент должен:
знать:
- определение радиана, формулы перевода градусной меры угла в радианную и обратно;
- определения синуса, косинуса, тангенса и котангенса числа;
- основные формулы тригонометрии; понятия обратных тригонометрических функций;
уметь:
- вычислять значения тригонометрических функций с заданной степенью точности;
- преобразовывать тригонометрические выражения, используя тригонометрические формулы.
Радианное измерение углов и дуг. Соотношения между градусной и радианной мерами угла. Синус, косинус, тангенс, котангенс числа. Тригонометрические функции числового аргумента, знаки их значений. Соотношения между тригонометрическими функциями одного аргумента. Формулы приведения. Четность и нечетность тригонометрических функций. Формулы сложения. Формулы двойного и половинного аргумента. Преобразования сумм тригонометрических функций в произведения. Преобразование произведений тригонометрических функций в суммы. Периодичность тригонометрических функций. Вычисление значений и тождественные преобразования тригонометрических выражений. Обратные тригонометрические функции.
Свойства и графики тригонометрических функций.
Студент должен:
знать:
- свойства и графики тригонометрических функций; свойства и графики обратных тригонометрических функций;
уметь:
- строить графики тригонометрических функций и на них иллюстрировать свойства функций;
- применять геометрические преобразования (сдвиг и деформацию) при построении графиков.
Свойства и графики тригонометрических функций. Построение геометрических преобразований (сдвига и деформации). Свойства и графики обратных тригонометрических функций.
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Производная функции
Студент должен:
знать:
- определение производной, ее геометрический и механический смысл;
- правила и формулы дифференцирования функций;
- определение второй производной, ее физический смысл;
- определение дифференциала функции.
уметь:
- дифференцировать функции, используя таблицу производных и правила дифференцирования, находить производные сложных функций;
- вычислять значение производной функции в указанной точке;
- находить угловой коэффициент и угол наклона касательной, составлять уравнение касательной и нормали к графику функции в данной точке;
- находить скорость изменения функции в точке;
- находить дифференциал функции.
Производная, ее геометрический и механический смысл. Производные суммы, произведения и частного двух функций. Производная степенной функции с натуральным показателем. Производная - тригонометрических функций. Правило дифференцирования сложной и обратной функций. Производные показательной, логарифмической и обратных тригонометрических функций. Вторая производная и ее физический смысл. Дифференциал функции.
Исследование функции с помощью производной.
Студент должен:
знать:
- необходимые и достаточные условия возрастания и убывания функции, существования экстремума;
- необходимые и достаточные условия выпуклости и вогнутости графика функции;
- определение точки перегиба;
- общую схему построения графиков функций с помощью производной;
- правило нахождения наибольшего и наименьшего значения функции на промежутке;
уметь:
- применять производную для нахождения промежутков монотонности и экстремумов функции;
- находить с помощью производной промежутки выпуклости и вогнутости графика функции, точки перегиба;
- проводить исследования и строить графики многочленов;
- находить наибольшее и наименьшее значения функции, непрерывной на промежутке,
Признаки возрастания и убывания функции. Экстремум функции. Исследование функции на экстремум. Выпуклость и вогнутость графика функции. Точки перегиба. Применение производной к построению графиков функции. Наибольшее и наименьшее значения функции на промежутке.
1111
6. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Неопределенный интеграл.
Студент должен:
знать:
- определение первообразной функции;
- определение неопределенного интеграла и его свойства; формулы интегрирования;
- способы вычисления неопределенного интеграла;
уметь:
- находить неопределенные интегралы, сводящиеся к табличным с помощью основных свойств и простейших преобразований;
- выделять первообразную функции, удовлетворяющую заданным начальным условиям;
- восстанавливать закон движения по заданной скорости, скорость по ускорению, количество электричества по силе тока и т.д.
Первообразная. Неопределенный интеграл и его свойства. Нахождение неопределенного интеграла. Приложение неопределенного интеграла к решению прикладных задач.
Определенный интеграл.
Студент должен:
знать:
- определение определенного интеграла, его геометрический смысл и свойства;
- способы вычисления определенного интеграла;
- понятие криволинейной трапеции, способы вычисления площадей криволинейных трапеций с помощью определенного интеграла;
- способы вычисления объемов тел вращения с помощью определенного интеграла;
уметь:
- вычислять определенный интеграл с помощью основных свойств и формулы Ньютона-Лейбница;
- находить площади криволинейных трапеций;
- находить объемы тел вращения;
- решать простейшие прикладные задачи, сводящиеся к нахождению интеграла.
Определенный интеграл и его геометрический смысл. Основные свойства определенного интеграла. Способы вычисления определенного интеграла. Вычисление площадей плоских фигур с помощью определенного интеграла. Вычисление объемов тел вращения.
Решение прикладных задач с помощью определенного интеграла.
ВЕКТОРЫ И КООРДИНАТЫ
Контрольная работа №1
Примеры решения упражнений
1) Вычислить:
а) 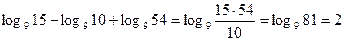
б) 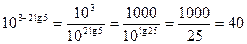
2) Решить уравнение:
а) 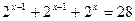 б)
б) 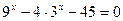
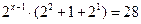
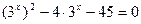
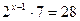
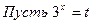
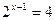
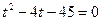
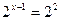

Функция y = 2t монотонна, значит 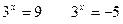
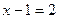
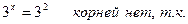
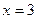

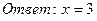
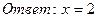
в) 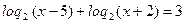
Область допустимых значений:
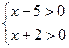
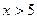
По свойству логарифма:
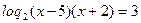
По определению логарифма:
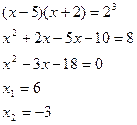
x 2 = -3 не удовлетворяет ОДЗ
Ответ. 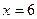
г) 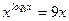
Область допустимых значений
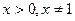
Прологарифмируем обе части уравнения по основанию 3:
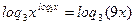
Применим свойства логарифма
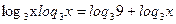
Пусть 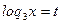
t2 = 2 + t
t2 – t – 2 = 0
t1 = 2 t2 = -1
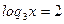
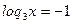
x1 = 32 x2 = 3-1
x1 = 9 x2 = 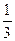
Ответ: x1 = 9, x2 = 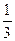 .
.
2) Решить неравенство:
а) 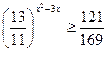
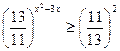
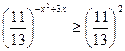
Т.к. 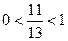 , то функция
, то функция 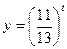 убывает:
убывает:
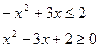

Решим неравенство методом интервалов:
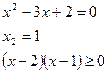
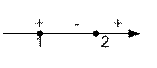
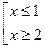
Ответ. 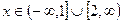

б)
|
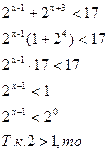

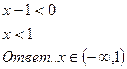
в) 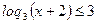

Область допустимых значений:
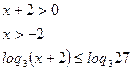
Т.к. 3>1, то функция y=loq3t возрастает:

Таким образом, исходное неравенство равносильно системе неравенств:
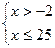
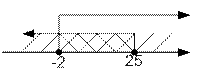
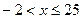
Ответ. 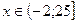
г) 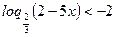
Область допустимых значений:
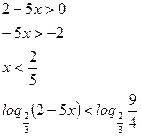
Т.к. 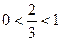 , то функция
, то функция 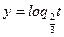 убывает:
убывает:
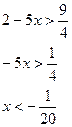
Таким образом, исходное неравенство равносильно системе неравенств:
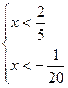
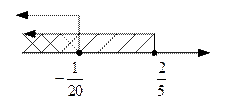
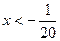
Ответ. 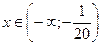
3.Вычислить 
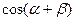 , если sin
, если sin 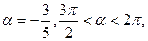 sin
sin 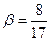 ,
, 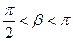
Дано:
sin 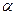 =
= 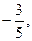
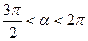

sin 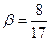 ,
, 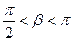
Найти: 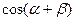
Решение: cos 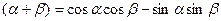 . Т.к.
. Т.к. 
4.Доказать тождество:а)
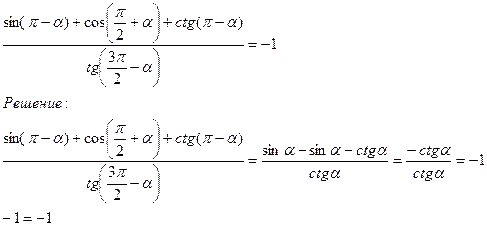
Что и требовалось доказать.
б)
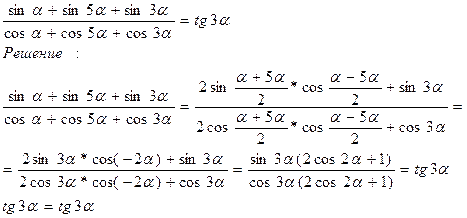
Что и требовалось доказать.
5.Решить уравнение:
a) 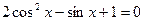
Решение:
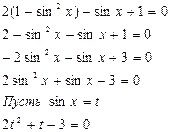
t 1 = - 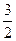
sin x = - 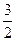
Корней нет, т.к. 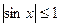
t 2 = 1
sin x = 1
x = 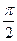 + 2
+ 2 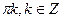
Ответ: x = 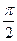 + 2
+ 2 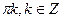
б) 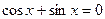
Решение:
Предположим, что cosx = 0. Тогда sinx = 0. Это противоречит основному тригонометрическому тождеству, т.к. 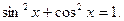 Значит,
Значит, 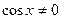
Разделим обе части исходного уравнения на cosx.
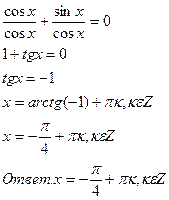
6.Решите задачу.
Прямоугольный треугольник с катетами 12см и 16см. Найдите расстояние от точки, до плоскости треугольника, если расстояния от этой точки до каждой вершины треугольника равны 26 см.
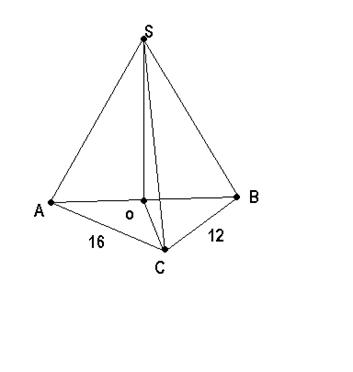
Дано:
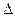 АВС-прямоугольный,
|AC|=16см, |BC|=12см.
|SA|=|SB|=|SC|=26см
Построение: АВС-прямоугольный,
|AC|=16см, |BC|=12см.
|SA|=|SB|=|SC|=26см
Построение:
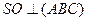 Т.к. |SA|=|SB|=|SC|, то
Т.к. |SA|=|SB|=|SC|, то  (по двум катетам). Значит, |AO|=|OB|=|OC|,
т.е О-центр описанной окружности около (по двум катетам). Значит, |AO|=|OB|=|OC|,
т.е О-центр описанной окружности около 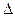 ABC, а т.к. ABC, а т.к. 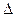 ABC-прямоугольный, то точка О-середина отрезка АВ.
Найти: |SO| ABC-прямоугольный, то точка О-середина отрезка АВ.
Найти: |SO|
|
Решение:
Рассмотрим 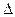 АВС. По теореме Пифагора |AB|=
АВС. По теореме Пифагора |AB|= 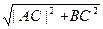
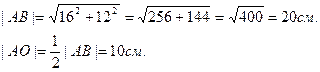
Рассмотрим 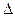 SOA-прямоугольный, т.к. SO
SOA-прямоугольный, т.к. SO 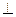 (ABC), по теореме Пифагора
(ABC), по теореме Пифагора
|SO|= 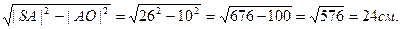
Ответ: |SO|=24 см.
Вариант 1
1) Вычислить:
а) 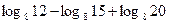
б) 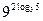
2) Решить уравнение:
а) 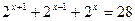
б) 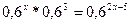
в) 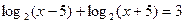
г) 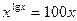
3) Решить неравенство:
а) 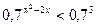
б) 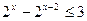
в) 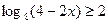
г) 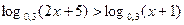
4.Вычислить sin( 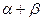 ), если sin
), если sin 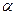 =-
=- 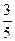 ,
, 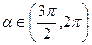 и sin
и sin 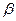 =
= 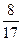 ,
, 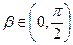 .
.
5.Доказать тождество:
a) 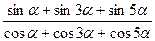 =tg3
=tg3 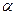 ;
;
b) 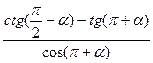 =0.
=0.
6.Решить уравнение:
a) 3cos2x – sin x – 1 =0;
b) cos x = sin x.
7.Катеты прямоугольного треугольника АВС равны 15 м и 20 м. Из вершины прямого угла С проведен к плоскости этого треугольника перпендикуляр CD=35 м. Найдите расстояние от точки D до гипотенузы АВ.
Вариант 2
1) Вычислить:
а) 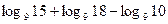
б) 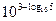
2) Решить уравнение:
а) 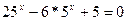
б) 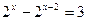
в) 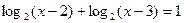
г) 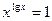
3) Решить неравенство: 
а) 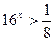
б) 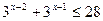
в) 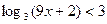
г) 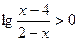
4.Вычислить cos( 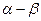 ), если cos
), если cos 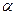 =
= 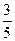 ,
, 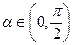 и cos
и cos 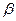 =-
=- 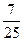 ,
, 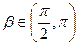 .
.
5.Доказать тождество:
a) 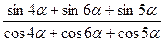 =tg5
=tg5 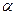 ;
;
b) cos( 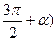 tg (
tg ( 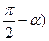 - sin (
- sin ( 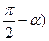 ) + ctg (
) + ctg ( 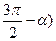 = tg
= tg 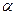
6.Решить уравнение:
a) 2 + cos2x – 2sin x =0;
b) sin2x – sin x cos x – 2 cos2 x = 0.
7.Стороны треугольника 10 см, 17 см и 21 см. Из вершины большего угла этого треугольника проведен перпендикуляр к его плоскости, равный 15 см. Определить расстояние от его концов до большей стороны.
Вариант 3
1) Вычислить:
а) 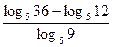
б) 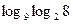
2) Решить уравнение:
а) 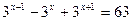
б) 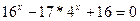
в) 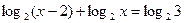
г) 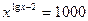
3) Решить неравенство: 
а) 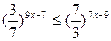
б) 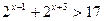
в) 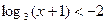
г) 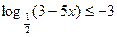
4.Вычислить sin( 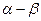 ), если sin
), если sin 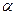 =-
=- 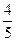 ,
, 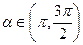 и cos
и cos 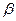 =-
=- 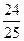 ,
, 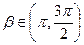 .
.
5.Доказать тождество:
a) 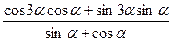 =cos
=cos 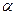 - sin
- sin 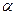 ;
;
b) 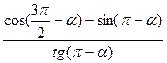 =2cos
=2cos 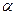 .
.
6.Решить уравнение:
a) sin2x – 3sin x cos x + 2 cos2 x = 0;
b) ccsx + cos3x = 4cos2x.
7.Из точки, отстоящей от плоскости на расстоянии 2 см, проведены две наклонные, образующие с плоскостью углы в 450, а между собой угол в 600. Найти расстояние между концами наклонных.
Вариант 4
1) Вычислить:
а) 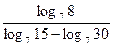
б) 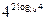
2) Решить уравнение:
а) 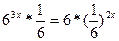
б) 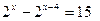
в) 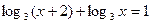
г) 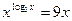
3) Решить неравенство:
а) 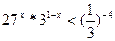
б) 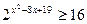
в) 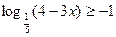
г) 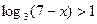
4.Вычислить cos 6300 – sin 14700 – ctg 11250.
5.Доказать тождество:
a) 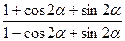 tg
tg  = 1;
= 1;
b) 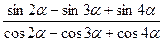 =tg3
=tg3  .
.
6.Решить уравнение:
c) 2sinx + sin2x = 0;
d) 3sin 2x - 5sinx -2 = 0.
7.Стороны треугольника равны 17, 15 и 8 см. Через вершину А меньшего угла треугольника проведена прямая АМ, перпендикулярная к его плоскости. Найти расстояние от точки М до прямой, содержащей меньшую сторону треугольника, если длина отрезка АМ равна 20 см.
Вариант 5
1) Вычислить:
а) 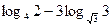
б) 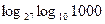
2) Решить уравнение:
а) 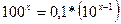
б) 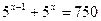
в) 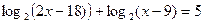
г) 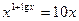
3) Решить неравенство:
а) 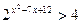
б) 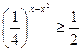
в) 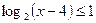
г) 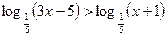
4.Вычислить sin2  , если cos
, если cos  =-
=- 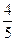 ,
, 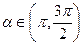 .
.
5.Доказать тождество:
a) 1 + cos 2  + 2 sin2
+ 2 sin2  = 2;
= 2;
b) 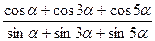 =ctg3
=ctg3  .
.
6.Решить уравнение:
a) 2sin2x + 3cos x = 0;
b) 2sin x + cos x = 0.
7.Из точки, отстоящей от плоскости на расстоянии 3 см, проведены две наклонные, образующие с плоскостью углы в 450 и 300, а между собой прямой угол. Найти расстояние между концами наклонных.
Вариант 6
1) Вычислить:
а) 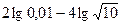
б) 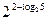
2) Решить уравнение:
а) 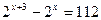
б) 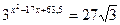
в) 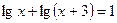
г) 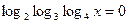
3) Решить неравенство:
а) 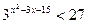
б) 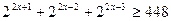
в) 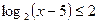
г) 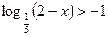
4.Вычислить sin(  +
+ 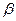 ), если cos
), если cos  =-
=- 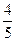 ,
, 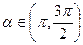 и sin
и sin 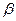 = -
= - 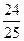 ,
, 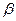
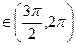 .
.
5.Доказать тождество:
a) 1 - cos( 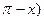 - sin(
- sin( 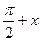 ) = 1;
) = 1;
b) sin( 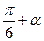 ) + sin(
) + sin( 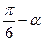 ) = cos
) = cos  .
.
6.Решить уравнение:
a) 1 + cosx + cos2x = 0;
b) sin2x + -3sin2x + 8cos2x = 0.
7.Из точки K, удаленной от плоскости  на 9 см, проведены к плоскости
на 9 см, проведены к плоскости  две наклонные KL и KM, образующие с плоскостью углы в 450 и 300 соответственно, а между собой прямой угол. Найти длину отрезка LM.
две наклонные KL и KM, образующие с плоскостью углы в 450 и 300 соответственно, а между собой прямой угол. Найти длину отрезка LM.
Вариант 7
1) Вычислить:
а) 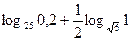
б) 
2) Решить уравнение:
а) 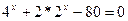
б) 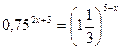
в) 
г) 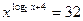
3) Решить неравенство:
а) 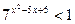
б) 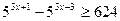
в) 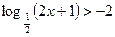
г) 
4.Вычислить cos( 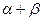 ), если sin
), если sin  =
= 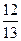 ,
, 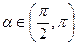 и sin
и sin 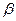 =-
=- 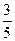 ,
, 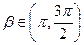 .
.
5.Доказать тождество:
a) 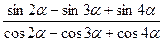 =tg3
=tg3  ;
;
b) tg(-  )ctg (
)ctg ( 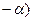 + cos2(
+ cos2( 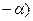 ) + sin2
) + sin2  = 2.
= 2.
6.Решить уравнениие:
a) cos( 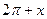 ) + 2sin(
) + 2sin( 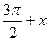 ) = 1;
) = 1;
b) 2sin x cos x – cos 5x sin2x = 0.
7.Из вершины прямого угла прямоугольного треугольника с катетами 15 см и 20 см проведен перпендикуляр длиной 16 см к плоскости треугольника. Найти расстояние от концов перпендикуляра до гипотенузы.
Вариант 8
1) Вычислить:
а) 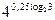
б) 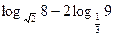
2) Решить уравнение:
а) 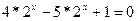
б) 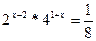
в) 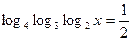
г) 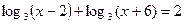
3) Решить неравенство:
а) 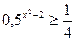
б) 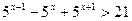
в) 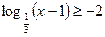
г) 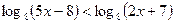
4.Вычислить tg5850 – cos10800 + cos15000.
5.Доказать тождество:
a) 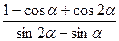 = ctg2
= ctg2  ;
;
b) 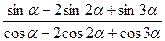 =tg2
=tg2  .
.
6.Решить уравнение:
a) cos 2x – sin2x – sin4xcos2x = 0;
b) sin(2700 - x) + sin(1800 - x) = 0.
7.Стороны треугольника равны 15, 37 и 44 см. Из вершины большего угла треугольника восстановлен к его плоскости перпендикуляр, равный 16 см. Найти расстояние от его концов до большей стороны.
Вариант 9
1) Вычислить:
а) 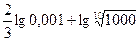
б) 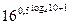
2) Решить уравнение:
а) 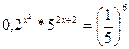
б) 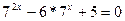
в) 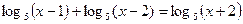
г) 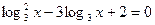
3) Решить неравенство:
а) 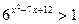
б) 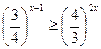
в) 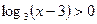
г) 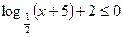
4.Вычислить cos8700 – sin12000 – 3tg5100.
5.Доказать тождество:
a) 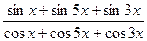 = tg3x;
= tg3x;
b) 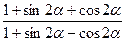 =ctg
=ctg  .
.
6.Решить уравнение:
a) cos5x + cos3x = cos4x;
b) sin2( 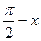 ) + sin(
) + sin( 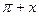 ) + 1 = 0.
) + 1 = 0.
7.Стороны треугольника равны 51, 30 и 27 см. Из вершины меньшего угла треугольника проведен к его плоскости перпендикуляр, равный 10 см. Найти расстояние от его концов до противоположной стороны треугольника.
Вариант 10
1) Вычислить:
а) 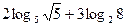
б) 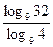
2) Решить уравнение:
а) 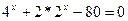
б) 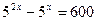
в) 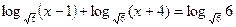
г) 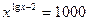
3) Решить неравенство:
а) 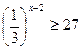
б) 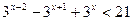
в) 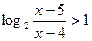
г) 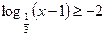
4.Вычислить cos( 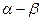 ), если sin
), если sin  =
= 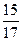 ,
, 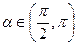 и cos
и cos 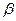 =-
=- 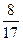 ,
, 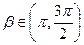 .
.
5.Доказать тождество:
a) 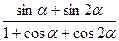 =tg
=tg  ;
;
b) 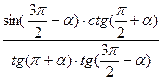 =sin
=sin  ;
;
6.Решить уравнениие:
a) 1 - cosx + sin 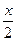 = 0;
= 0;
b) sin2x + sin2x = 3cos2x;
7.В треугольнике АВС длина отрезка АВ равна 13 см, длина отрезка ВС равна 14 см, длина отрезка АС равна 15 см. Из вершины А восстановлен к плоскости треугольника перпендикуляр AD, равный 5 см. Найти расстояние от точки D до стороны ВС.
Контрольная работа №2
Примеры решения упражнений
- Дана функция
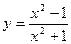 . Найдите
. Найдите 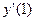 .
.
Решение:
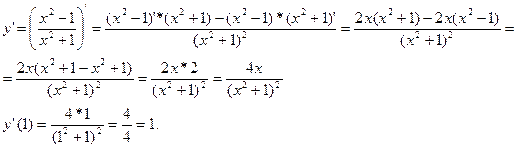
Ответ: 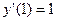
- Дана функция y=lncosx . Найдите
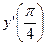
Решение:
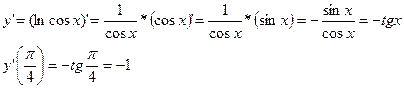
Ответ. 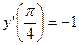
- Найдите экстремумы функции:
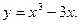
Решение:
Найдем производную функции:
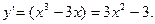
Найдем критические точки:
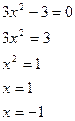
Исследуем знак производной на промежутках, на которые найденные критические точки делят область определения функции:





 + - + y/
+ - + y/
-1 1 y
x = -1 – точка максимума
x = 1 – точка минимума
Найдём значение функции 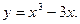 в найденных точках:
в найденных точках:
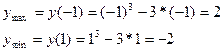
Ответ. max (-1,2), min (1,2)
- Постройте график функции:
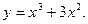
1) Найдем область определения функции:

2) Данная функция не является ни четной, ни нечетной, ни периодической.
3) Найдем область пересечения с осями координат:
С осью Ox:
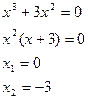
С осью Oy:
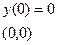
4) Найдем экстремумы функции:



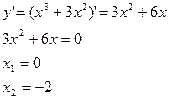
+ - + y/
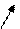
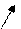

-2 0 y
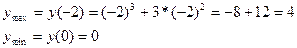
5) Найдём точки перегиба:

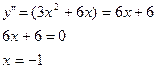 y
y

 - +
- +

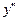
 4
4
-1
 2 2
2 2




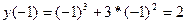
6) Построим график функции: -3-2-1 1
- В прямом параллелепипеде стороны основания равны
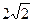 см и 5см и образуют угол в
см и 5см и образуют угол в 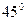 , меньшая диагональ параллелепипеда равна 7 см.
, меньшая диагональ параллелепипеда равна 7 см.
Найдите длину бокового ребра параллелепипеда.
B1 C1
 A1 D1
B C
A D
A1 D1
B C
A D
|
Дано:
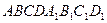 - прямой параллелепипед .
|AB|= - прямой параллелепипед .
|AB|= 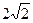 см., |AD|=5 см., см., |AD|=5 см., 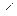 BAD= BAD= 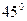 ; | ; | 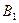 D|=7 см.
Найти. |B D|=7 см.
Найти. |B 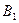 | |
|
Решение:
Рассмотрим треугольник ABD.
По теореме косинусов:
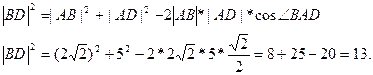
Рассмотрим треугольник 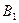 BD- прямоугольный;
BD- прямоугольный;
Т.к. параллелепипед прямой то по теореме Пифагора:
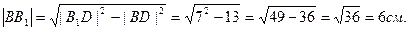
Ответ: | 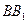 | = 6 см.
| = 6 см.
- Основанием пирамиды является треугольник со сторонами 39 см, 17 см, 28см, боковые рёбра равны каждое 22,9 см.
Найдите высоту пирамиды.
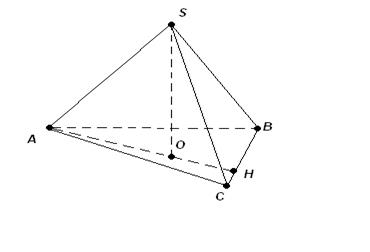
| Дано:
SABC-пирамида, |AB|=39 см, |BC|=17 cм, |AC|=28 см,
|SA|=|SB|=|SC|=22,9 см.
Построение:
 Т.к. |SA|=|SB|=|SC| то, О-центр описанной около
Т.к. |SA|=|SB|=|SC| то, О-центр описанной около  АВС окружности.
Найти |SO|. АВС окружности.
Найти |SO|.
|
Решение:
Рассмотрим  АВС. Найдём площадь этого треугольника по формуле Герона:
АВС. Найдём площадь этого треугольника по формуле Герона:
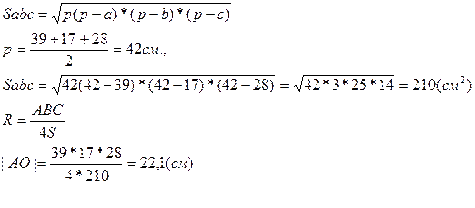
Рассмотрим  SOA-прямоугольный, т.к.
SOA-прямоугольный, т.к.  .
.
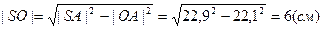
Ответ. |SO| = 6 см.
- Образующая конуса равна 6 см и наклонена к плоскости основания под углом 600. Найдите высоту конуса.
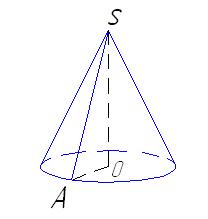
| Дано:
Конус, |SA|=6 см,  SAO= SAO= 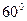 .
Найти |SO|. .
Найти |SO|.
|
Решение:
Рассмотрим 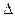 SOА - прямоугольный.
SOА - прямоугольный.
sin 60 0 = 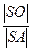
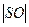 =
= 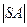 sin 60 0 = 6
sin 60 0 = 6 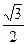 = 3
= 3 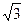 см.
см.
Ответ. |SO| = 3 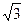 см.
см.
8.Найдите дифференциал функции y = etgx.
Решение:
dy = (etgx)/ dx = 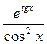 dx.
dx.
9.Найдите все первообразные функции:
а) y = 6sinx + 5
Решение:
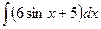 =
= 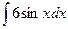 +
+ 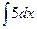 = -6cosx + 5x + C
= -6cosx + 5x + C
б) y = 2x4
Решение:
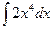 =
= 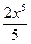 + C
+ C
в) y = 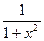 - 4x
- 4x
Решение:
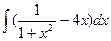 =
= 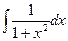 -
- 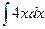 = arctg x -
= arctg x - 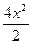 + C = arctg x – 2x2 + C
+ C = arctg x – 2x2 + C
10.Вычислите определенный интеграл:
а) 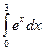
Решение:
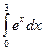 = ex
= ex 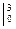 = e3 – e0 = e3 – 1
= e3 – e0 = e3 – 1
б) 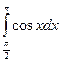
Решение:
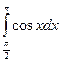 = sinx
= sinx 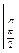 = sin
= sin 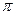 - sin
- sin 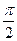 = 0 – 1 = -1
= 0 – 1 = -1
в) 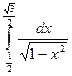
Решение:
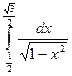 = arcsinx
= arcsinx 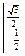 = arcsin
= arcsin 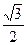 - arcsin
- arcsin 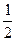 =
= 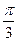 -
- 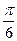 =
= 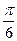
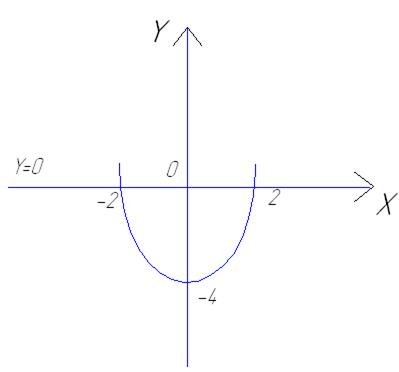
11.Найдите площадь фигуры, ограниченной линиями y = x2 – 4 и y = 0.
Дано:
y = x2 – 4
y = 0
Найти Sфигуры
Решение:
S = 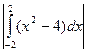 = = 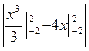 = = = = 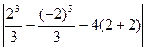 = = 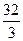 = =10 = =10 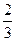 (кв.ед.)
Ответ. Площадь фигуры равна 10 (кв.ед.)
Ответ. Площадь фигуры равна 10  (кв.ед.) (кв.ед.)
| 
|
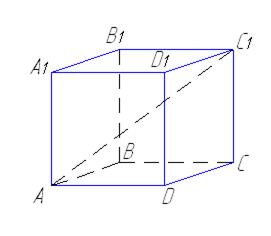
12.В прямом параллелепипеде стороны основания равны 1 м и 2 м и образуют угол в 600. Большая диагональ параллелепипеда равна 4 м. Найдите объем и боковую поверхность параллелепипеда.
 Решение:
V = Soh; Sбок = Роснh
So=
Решение:
V = Soh; Sбок = Роснh
So= 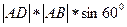 = 2 = 2  1 1  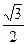 = = 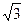 (м2)
По теореме косинусов: (м2)
По теореме косинусов: 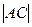 2 = 2 = 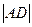 2 + 2 + 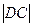 2 – 2 2 – 2  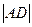  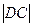  cos1200 = 22 + 12 – 2 cos1200 = 22 + 12 – 2  2 2  1 1  (- (- 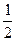 ) = 7 (м2)
Рассмотрим прямоугольный треугольник ACC1. По теореме Пифагора: ) = 7 (м2)
Рассмотрим прямоугольный треугольник ACC1. По теореме Пифагора: 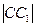 = = 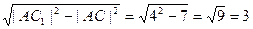 (м).
V = (м).
V = 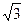  3 = 3 3 = 3 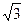 (м3).
Sбок = (2+1) (м3).
Sбок = (2+1)  2 2  3 = 18 (м2).
Ответ. V = 3 3 = 18 (м2).
Ответ. V = 3 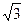 (м3), Sбок = 18 (м2). (м3), Sбок = 18 (м2).
| Дано:
ABCDA1B1C1D1 – прямой параллелепипед
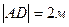 , , 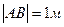 , , 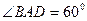 , , 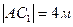 .
Найти: V, Sбок .
Найти: V, Sбок
|
13.Площадь основания конуса равна 16  дм2, а боковая поверхность 20
дм2, а боковая поверхность 20  дм2 . Найдите объем конуса.
дм2 . Найдите объем конуса.
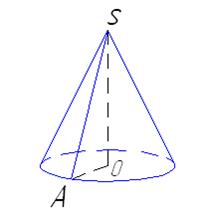 Дано: конус;
So = 16 Дано: конус;
So = 16  дм2, Sбок = 20 дм2, Sбок = 20  дм2.
Найти: V дм2.
Найти: V
|
Решение:
V = 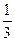 Soh;
Soh;
Так как в основании конуса лежит круг, то 
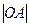 2 = 16
2 = 16  ;
;
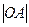 2 = 16;
2 = 16;
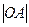 = 7 (дм).
= 7 (дм).
Sбок = 

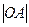

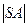 .
.
Подставим в формулу 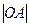 = 4, Sбок = 20
= 4, Sбок = 20 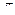 .
.

 4
4 
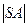 = 20
= 20  ;
;
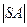 = 5 (дм).
= 5 (дм).
Рассмотрим прямоугольный треугольник SOA. По теореме Пифагора |SO|= 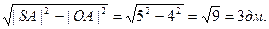
V = 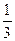
 16
16 
 3 = 16
3 = 16  (дм3).
(дм3).
Ответ. V = 16  (дм3).
(дм3).
Вариант 1
1. Дана функция y= 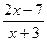 . Найдите y'(-2)
. Найдите y'(-2)
2. Дана функция y=ln sin x. Найдите y' (-π/4)
3. Найдите экстремумы функции: y = 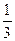 x3 – 2x2.
x3 – 2x2.
4. Постройте график функции: y =2x2 – 8x.
5. В прямом параллелепипеде стороны основания равны 3см и 5см и образуют угол в 60◦. Площадь большого диагонального сечения равна 63 см2. Найдите боковое ребро параллелепипеда.
6. Основанием пирамиды служит прямоугольный треугольник, катеты которого 15 см и 20 см, каждая боковая грань наклонена к основанию под углом 60◦. Найдите высоту пирамиды.
7. Площадь осевого сечения цилиндра равна 10 м2, а площадь основания - 4  м2. Найдите высоту цилиндра.
м2. Найдите высоту цилиндра.
8. Найдите дифференциал функции y = (1 – x2)5.
9. Найдите все первообразные функции:
a) y = 5sinx – 4 б) y = x2 в) y = 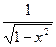 +x
+x
10. Вычислите определенный интеграл:
a) 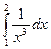 б)
б) 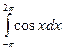 в)
в) 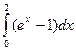
11. Найдите площадь фигуры, ограниченной линиями:
y = 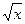 +1, y = 0, x = 0, x = 1.
+1, y = 0, x = 0, x = 1.
12. Основанием пирамиды служит прямоугольный треугольник, катеты которого 15 см и 20 см, каждая боковая грань наклонена к основанию под углом 45◦. Найдите площадь боковой поверхности и объем пирамиды.
13. Высота и образующая конуса относятся как 35:37. Полная поверхность конуса равна 588  см2. Найдите площадь боковой поверхности и объем конуса.
см2. Найдите площадь боковой поверхности и объем конуса.
Вариант 2
1. Дана функция y= 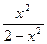 . Найдите y'(1)
. Найдите y'(1)
2. Дана функция y=ctg 4x. Найдите y' ( 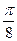 )
)
3. Найдите экстремумы функции: y =2x4 – x
4. Постройте график функции: y = - 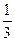 х3 + х2 - 6.
х3 + х2 - 6.
5. Стороны основания прямой треугольной призмы равны 3 см, 25 см и 26 см, а площадь большей боковой грани равна 260 см2. Найдите боковое ребро призмы.
6. Основание пирамиды – треугольник со сторонами, равными 6 см, 10 см и 14 см. каждый двугранный угол при основании равен 30◦. Найдите высоту пирамиды.
7. Высота конуса равна 15 см, а радиус основания равен 8 см. Найдите образующую конуса.
8. Найдите дифференциал функции y = ln sinx.
9. Найдите все первообразные функции:
a) y = cosx + 2 б) y = 4x3 в) y = 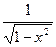 - x
- x
10. Вычислите определенный интеграл:
a) 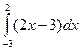 б)
б) 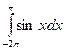 в)
в) 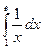
11. Найдите площадь фигуры, ограниченной линиями:
y = 4 – x2, y = 0.
12. В прямом параллелепипеде стороны основания равны 3 дм и 8 дм, угол между ними 600. Зная, что большая диагональ параллелепипеда равна 49 дм, найдите боковую поверхность и объем параллелепипеда.
13. Радиусы оснований усеченного конуса и его высота относятся как 3:6:4. Вычислите боковую поверхность и объем конуса, если его образующая равна 25 см.
Вариант 3
1. Дана функция y= 5х ∙ х5 . Найдите y'(0)
2. Дана функция y=еtgx . Найдите y' (0)
3. Найдите экстремумы функции: y = 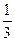 х3 – х2
х3 – х2
4. Постройте график функции: y =х3 - 6х + 16
5. Основание прямого параллелепипеда параллелограмм со сторонами 8 см и 32 см и острым углом 60◦. Большая диагональ параллелепипеда равна 40 см. Найдите высоту параллелепипеда.
6. Основание пирамиды – равнобедренный треугольник, у которого основание равно 6 см, а высота 9 см, боковые ребра равны между собой, и каждое содержит 13 см. Найдите высоту пирамиды.
7. Образующая конуса равна 12 см и наклонена к плоскости основания под углом 300. Найдите радиус основания конуса.
8. Найдите дифференциал функции y = ln cosx.
9. Найдите все первообразные функции:
a) y = 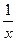 б) y = 6x4 в) y =
б) y = 6x4 в) y = 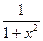 +2
+2
10. Вычислите определенный интеграл:
a) 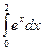 б)
б) 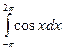 в)
в) 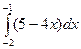
11. Найдите площадь фигуры, ограниченной линиями:
y = 9 – x2, y = 0.
12. Основанием пирамиды служит прямоугольный треугольник, катеты которого 15 см и 20 см, каждая боковая грань наклонена к основанию под углом 600. Найдите полную поверхность пирамиды и объем.
13. Высота усеченного конуса равна 3 см. Радиус одного основания вдвое больше радиуса другого, а образующая наклонена к основанию под углом 450. Найдите боковую поверхность и объем этого конуса.
Вариант 4
1. Дана функция y= 4х3 – 5х2 + 1. Найдите y'(1).
2. Дана функция y=е sinx. Найдите y' (0)
3. Найдите экстремумы функции: y =2х3– 9х2 + 12х – 8
4. Постройте график функции: y =3х3 - х
5. Стороны прямого параллелепипеда равны 5см и 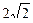 см, образуют угол 45◦ . Меньшая диагональ параллелепипеда равна 7см. Найдите боковое ребро параллелепипеда.
см, образуют угол 45◦ . Меньшая диагональ параллелепипеда равна 7см. Найдите боковое ребро параллелепипеда.
6. Основанием пирамиды служит равнобедренный треугольник, основание которого 12см и высота 18см. каждое из боковых ребер равно 26см. найдите высоту пирамиды.
7. Шар радиуса 41 дм пересечен плоскостью, находящейся на расстоянии 9 дм от центра. Найдите площадь сечения.
8. Найдите дифференциал функции y = sin 2 x.
9. Найдите все первообразные функции:
a) y = x3 б) y = 2 x - 1 в) y = 5sin x +2x
10. Вычислите определенный интеграл:
a) 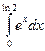 б)
б) 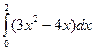 в)
в) 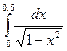
11. Найдите площадь фигуры, ограниченной линиями:
y = x2- 3, y = 0.
12. Основанием пирамиды служит треугольник со сторонами, равными 6 см, 10 см, 14 см. Каждый двугранный угол при основании равен 300. Найдите площадь боковой поверхности и объем этой пирамиды.
13. Боковая поверхность конуса 15 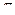 дм2, а полная поверхность 24
дм2, а полная поверхность 24 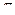 дм2. Найдите объем конуса.
дм2. Найдите объем конуса.
Вариант 5
1. Дана функция y= 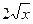 - 3. Найдите y'(1).
- 3. Найдите y'(1).
2. Дана функция y=5 sinx. Найдите y' (0).
3. Найдите экстремумы функции: y =2х3– 3х2 - 12х + 8
4. Постройте график функции: y = - х3 +3х
5. В прямой треугольной призме стороны основания равны 17см, 10см и 9см, а площадь меньшей боковой грани равна 90 см2. Найдите высоту призмы.
6. Основание пирамиды – прямоугольник со сторонами 6см и 8 см, каждое боковое ребро пирамиды равно 13 см. Найдите высоту пирамиды.
7. Найдите образующую усеченного конуса, если радиусы оснований равны 3 см и 6 см, а высота равна 4 см.
8. Найдите дифференциал функции y = cos 2 x.
9. Найдите все первообразные функции:
a) y = 5 x + e x б) y = x 5 в) y = 4 cos x – 3x2
10. Вычислите определенный интеграл:
a) 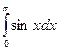 б)
б) 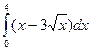 в)
в) 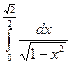
11. Найдите площадь фигуры, ограниченной линиями:
y = x2- 8, y = 0.
12. В основании пирамиды лежит равнобедренный треугольник, основание которого равно 12 дм, а боковая сторона 10 дм. Все боковые грани образуют с основанием углы 450. Найдите площадь боковой поверхности и объем пирамиды.
13. Образующая усеченного конуса равна 4 см и наклонена к плоскости основания под углом 600. Зная, что радиус большего основания равен 5 см, найдите боковую поверхность и объем усеченного конуса.
Вариант 6
1. Дана функция y = 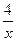 + 5х2. Найдите y'(1).
+ 5х2. Найдите y'(1).
2. Дана функция y = sin7х. Найдите y' (0).
3. Найдите экстремумы функции: y =2х3 + 9x2 + 12x
4. Постройте график функции: y = 9x - 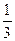 x3
x3
5. В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 300. Найдите высоту параллелепипеда.
6. Основанием пирамиды DABC служит треугольник со сторонами AB=AC=13см, BC=10см, ребро AD перпендикулярно к плоскости основания и равно 9 см. Найдите высоту грани DBC.
7. Угол между образующей и осью конуса равен 450, образующая равна 6,5 см. Найдите радиус основания конуса.
8. Найдите дифференциал функции y = arcsin x2.
9. Найдите все первообразные функции:
a) y = 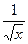 б) y = 2sinx + 1 в) y = 3x + cos x
б) y = 2sinx + 1 в) y = 3x + cos x
10. Вычислите определенный интеграл:
a) 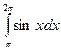 б)
б) 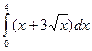 в)
в) 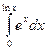
11. Найдите площадь фигуры, ограниченной линиями:
y = x2 + 1, y = 0, x = -1, x = 2.
12. Основание пирамиды – равнобедренный треугольник, у которого основание равно 6 см, а высота 9 см, боковые ребра равны между собой и каждое содержит 13 см. Найдите объем пирамиды.
13. Высота усеченного конуса равна 3 см. Радиус одного основания вдвое больше другого, а образующая наклонена к основанию под углом 450. Найдите площадь боковой поверхности и объем этого конуса.
Вариант 7
1. Дана функция y=3х3 – 4х +1. Найдите y'(1).
2. Дана функция y = ln5х. Найдите y' (-2).
3. Найдите экстремумы функции: y = 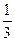 х3 - 4х
х3 - 4х
4. Постройте график функции: y = -0,5х2 + х + 1,5
5. Основанием прямоугольного параллелепипеда является параллелограмм со сторонами 3дм и 8дм, угол между ними 60◦. Найдите боковое ребро параллелепипеда, если большая диагональ параллелепипеда 49 дм.
6. Основанием пирамиды служит равнобедренный треугольник, у которого основание равно 12см, а боковая сторона 10 см. Боковые грани образуют с основанием равные углы по 45◦ . Найдите высоту пирамиды.
7. Радиусы оснований усеченного конуса равны 5 см и 11 см, образующая равна 10 см. Найдите высоту усеченного конуса.
8. Найдите дифференциал функции y = arccos 2x.
9. Найдите все первообразные функции:
a) y = 3cosx – 4sinx б) y = 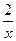 в) y =
в) y = 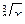
10. Вычислите определенный интеграл:
a) 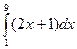 б)
б) 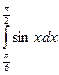 в)
в) 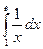
11. Найдите площадь фигуры, ограниченной линиями:
y = x3, y = 0, x = -1, x = 2.
12. Стороны прямого параллелепипеда равны 5 см и 2 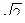 см, образуют угол 450, меньшая диагональ параллелепипеда равна 7 см. Найдите площадь полной поверхности и объем параллелепипеда.
см, образуют угол 450, меньшая диагональ параллелепипеда равна 7 см. Найдите площадь полной поверхности и объем параллелепипеда.
13. Площадь основания конуса 9 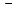 см2 , полная поверхность его 24
см2 , полная поверхность его 24 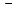 см2 . Найдите объем конуса.
см2 . Найдите объем конуса.
Вариант 8
1. Дана функция y=(3х2 – 2) (2 + 3х2). Найдите y'(-1).
2. Дана функция y = tg3х. Найдите y' (0).
3. Найдите экстремумы функции: y = - х3 + 2х2 – 8x + 1
4. Постройте график функции: y = 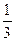 х3 - 9х
х3 - 9х
5. В прямоугольном параллелепипеде стороны основания равны 3см и 4см. Диагональ параллелепипеда образует с плоскостью основания угол в 45◦ . Найдите высоту параллелепипеда.
6. В основании пирамиды лежит прямоугольный треугольник с катетами 12см и 16см. Длина каждого бокового ребра равна 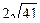 см. Найдите высоту пирамиды.
см. Найдите высоту пирамиды.
7. Образующая конуса, равная 10 см, наклонена к плоскости основания под углом 300. Найдите радиус основания конуса.
8. Найдите дифференциал функции y = e sinx.
9. Найдите все первообразные функции:
a) y = 2x – x2 б) y = 4sinx + 3 в) y = 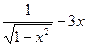
10. Вычислите определенный интеграл:
a) 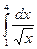 б)
б) 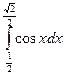 в)
в) 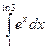
11. Найдите площадь фигуры, ограниченной линиями:
y = x3, y = 0, x = -2, x = 1.
12. Основание пирамиды – прямоугольник со сторонами 6 см и 8 см, каждое боковое ребро пирамиды равно 13 см. Найдите объем пирамиды.
13. Высота цилиндра на 10 см больше радиуса его основания, площадь полной поверхности равна 264  см2. Найдите площадь боковой поверхности и объем цилиндра.
см2. Найдите площадь боковой поверхности и объем цилиндра.
Вариант 9
1. Дана функция y= 5x + x5. Найдите y'(1).
2. Дана функция y = sin3х. Найдите y' (0).
3. Найдите экстремумы функции: y = -х4 + 4х - 4.
4. Постройте график функции: y = 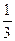 х3 - 2х2.
х3 - 2х2.
5. В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 450. Найдите боковое ребро параллелепипеда.
6. Боковое ребро и апофема правильной треугольной пирамиды соответственно равны 10 см и 6 см. Найдите стороны основания этой пирамиды.
7. Образующая конуса наклонена к плоскости основания под углом 300. Найдите образующую, если радиус основания конуса равен 6 см..
8. Найдите дифференциал функции y = e cosx.
9. Найдите все первообразные функции:
a) y = x3 + 3 б) y = 2sinx – 4x в) y = 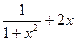
10. Вычислите определенный интеграл:
a) 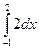 б)
б) 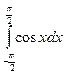 в)
в) 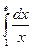
11. Найдите площадь фигуры, ограниченной линиями:
y = x2 – 4x + 3, y = 0.
12. В правильной четырехугольной усеченной пирамиде стороны оснований 16 м и 4 м. Найдите площадь полной поверхности и объем, если высота пирамиды равна 8 м.
13. Радиусы оснований усеченного конуса 6 м и 2 м, образующая наклонена к основанию под углом 450. Найдите площадь боковой поверхности и объем конуса.
Вариант 10
1. Дана функция y= 2 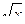 - x4. Найдите y'(1).
- x4. Найдите y'(1).
2. Дана функция y = cos2х. Найдите y' (0).
3. Найдите экстремумы функции: y = 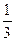 x3 -
x3 - 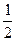 х2 + 6.
х2 + 6.
4. Постройте график функции: y = х3 - 3х.
5. Основание прямой призмы – треугольник со сторонами 5 см и 3 см и углом 1200 между ними. Наибольшая из площадей боковых граней равна 35 см2. Найдите высоту призмы.
6. Основанием пирамиды является треугольник со сторонами 10 см, 10 см и 12 см. Каждая боковая грань наклонена к основанию под углом 450. Найдите высоту пирамиды.
7. Шар пересекает плоскость на расстоянии 9 см от центра, площадь сечения 1600  см2. Найдите радиус шара.
см2. Найдите радиус шара.
8. Найдите дифференциал функции y = 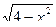
9. Найдите все первообразные функции:
a) y = 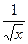 б) y = 3x2 + 1 в) y = 2x -
б) y = 3x2 + 1 в) y = 2x - 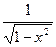
10. Вычислите определенный интеграл:
a) 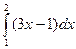 б)
б) 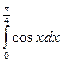 в)
в) 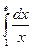
11. Найдите площадь фигуры, ограниченной линиями:
y = x2 + x - 6, y = 0.
12. В прямоугольном параллелепипеде стороны основания равны 12 см и 5 см. Диагональ параллелепипеда образует с плоскостью основания угол в 300. Найдите площадь полной поверхности и объем параллелепипеда.
13. Поверхность шара равна 225  м2. Определите его объем.
м2. Определите его объем.
Литература
Основные источники:
1. Атанасян Л.С. Геометрия (10-11 класс) - учебник для
общеобразовательных учреждений. Просвещение. 2008 г.
2. Богомолов Н.Б. Практические занятия по математике: учебное пособие
для студентов средних специальных учебных заведений.
Высш. шк., 2007г.
3. Богомолов Н.Б., П.И.Самойленко Математика: учебник для студентов
образовательных учреждений среднего профессионального образования.
Дрофа, 2006г.
4. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в
упражнениях и задачах (в двух частях), 2006г.
5. Омельченко В.П., Курбатова Э.В. Математика: учебное пособие для
студентов образовательных учреждений среднего профессионального
образования. – Ростов н/Д: Феникс, 2007г.
Дополнительные источники:
1. Григорьев В.П., Ю.А.Дубинский Элементы высшей математики:
учебник для студентов образовательных учреждений среднего
профессионального образования. Издательский центр «Академия»,
2004г.
2. Саакян С.М., А.М.Гольдман, Д.В.Денисов Задачи по алгебре и началам
анализа: пособие для учащихся 10 – 11 кл. Просвещение, 2005г.
3. Шипачев С.М. Начала высшей математики: пособие для вузов. Дрофа,
2002г.
Интернет-ресурсы:
1. http://en.edu/ru – естественнонаучный портал;
2. http://schools.techno.ru – сайт «Школы в Интернете»
3. http://www.school.edu.ru – российский образовательный портал
4. http://www.alleng.ru- сайт «Образовательные ресурсы Интернета
школьникам и студентам»
Нижнетагильский машиностроительный техникум
УТВЕРЖДАЮ
И.о. директора техникума
____________ Е.В. Гильдерман
« ___»_____________201 г.
Методические рекомендации
по выполнению домашней контрольной работы
для студентов заочной формы обучения
по дисциплине
«МАТЕМАТИКА»
основной образовательной программы
среднего (полного) общего образования
технический профиль,
базовый уровень
Нижний Тагил,
2017
Методические рекомендации разработаны в соответствии с рабочей программой учебной дисциплины «Математика», разработанной на основе Федерального государственного образовательного стандарта среднего (полного) общего образования, утвержденного приказом Министерства образования и науки Российской Федерации от 17 мая 2012 года № 413 и примерной программой, рекомендованной ФГАУ «ФИРО» для реализации основной профессиональной образовательной программы СПО протокол № 3 от 21.07.2015г.
| Организация разработчик: | ФГАОУ ВО «Уральский федеральный университет имени первого Президента России Б.Н. Ельцина» Нижнетагильский технологический и институт Нижнетагильский машиностроительный техникум |
| Разработчик: | преподаватель НТМТ Ведерникова Е.В. |
Методические рекомендации обсуждены и одобрены на заседании цикловой комиссии общеобразовательного, социально-экономического, математического и естественнонаучного цикла
| Протокол № ____ «___» _______ 201 г. | Председатель ЦК Ведерникова Е.В. |
Содержание
Введение
1. Пояснительная записка
1.1 Результаты освоения дисциплины
1.2 Основные понятия, необходимые для выполнения ДКР
1.3 Примеры решения задач
2. Задания для домашней контрольной работы
3. Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы.
Пояснительная записка
1.1 Результаты освоения дисциплины «Математика».
Тематический план и содержание учебной дисциплины соответствует рабочей программе учебной дисциплины «Математика» и обеспечивает достижение студентами следующих результатов:
• личностных:
−− сформированность представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, идеях и методах математики;
−− понимание значимости математики для научно-технического прогресса, сформированность отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей;
−− развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, для продолжения образования и самообразования;
−− овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для освоения смежных естественно-научных дисциплин и дисциплин профессионального цикла, для получения образования в областях, не требующих углубленной математической подготовки;
−− готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности;
−− готовность и способность к самостоятельной творческой и ответственной деятельности;
−− готовность к коллективной работе, сотрудничеству со сверстниками в образовательной, общественно полезной, учебно-исследовательской, проектной и других видах деятельности;
−− отношение к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем;
• метапредметных:
−− умение самостоятельно определять цели деятельности и составлять планы деятельности; самостоятельно осуществлять, контролировать и корректировать деятельность; использовать все возможные ресурсы для достижения поставленных целей и реализации планов деятельности; выбирать успешные стратегии в различных ситуациях;
−− умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности, эффективно разрешать конфликты;
−− владение навыками познавательной, учебно-исследовательской и проектной деятельности, навыками разрешения проблем; способность и готовность к самостоятельному поиску методов решения практических задач, применению различных методов познания;
−− готовность и способность к самостоятельной информационно-познавательной деятельности, включая умение ориентироваться в различных источниках информации, критически оценивать и интерпретировать информацию, получаемую из различных источников;
−− владение языковыми средствами: умение ясно, логично и точно излагать свою точку зрения, использовать адекватные языковые средства;
−− владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств для их достижения;
−− целеустремленность в поисках и принятии решений, сообразительность и интуиция, развитость пространственных представлений; способность воспринимать красоту и гармонию мира;
• предметных:
−− сформированность представлений о математике как части мировой культуры и месте математики в современной цивилизации, способах описания явлений реального мира на математическом языке;
−− сформированность представлений о математических понятиях как важнейших математических моделях, позволяющих описывать и изучать разные процессы и явления; понимание возможности аксиоматического построения математических теорий;
−− владение методами доказательств и алгоритмов решения, умение их применять, проводить доказательные рассуждения в ходе решения задач;
−− владение стандартными приемами решения рациональных и иррациональных, показательных, степенных, тригонометрических уравнений и неравенств, их систем; использование готовых компьютерных программ, в том числе для поиска пути решения и иллюстрации решения уравнений и неравенств;
−− сформированность представлений об основных понятиях математического анализа и их свойствах, владение умением характеризовать поведение функций, использование полученных знаний для описания и анализа реальных зависимостей;
−− владение основными понятиями о плоских и пространственных геометрических фигурах, их основных свойствах; сформированность умения распознавать геометрические фигуры на чертежах, моделях и в реальном мире; применение изученных свойств геометрических фигур и формул для решения геометрических задач и задач с практическим содержанием;
−− сформированность представлений о процессах и явлениях, имеющих вероятностный характер, статистических закономерностях в реальном мире, основных понятиях элементарной теории вероятностей; умений находить и оценивать вероятности наступления событий в простейших практических ситуациях и основные характеристики случайных величин;
−− владение навыками использования готовых компьютерных программ при решении задач.
Методические рекомендации
Работа студента над курсом математики на заочном отделении НТМТ предполагает самостоятельное изучение теоретического материала и выполнение значительного числа задач и упражнений, позволяющих глубже понять содержание курса и выработать необходимые навыки в выполнении стандартных математических операций. Этой цели служит контрольная работа, которую студент должен выполнить в течение семестра.
В данном методическом руководстве содержатся методические указания, необходимые для выполнения работы, а также варианты заданий для выполнения работы. Вариант контрольной работы студент выбирает по последней цифре номера студенческого билета.
При выполнении контрольной работы и представлении ее на проверку студент должен руководствоваться следующими правилами.
1. Каждая контрольная работа должна быть выполнена в отдельной тетради и сдана на проверку на заочное отделение в срок, установленный в индивидуальном графике студента.
2. Если при проверке контрольной работы обнаружены ошибки, то студент должен выполнить работу над ошибками и сдать ее для повторной проверки.
3. Решение задач из контрольной работы должно быть достаточно подробным и логически последовательным. Полезно в тексте решения приводить формулировки теорем и других теоретических сведений, на основании которых делаются Ваши заключения.
Студент – заочник должен иметь в виду, что вдумчивая самостоятельная работа над контрольными заданиями является залогом успешной сдачи зачета по математике.
1 ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Действительные числа. Приближенные вычисления и вычислительные средства.
Студент должен:
знать:
- определение действительного числа, абсолютной и относительной погрешности приближений;
- практические приемы вычислений с приближенными данными;
уметь:
- выполнять с заданной точностью на инженерном или программируемом (в режиме вычислений) микрокалькуляторе арифметические действия;
- вычислять значения элементарных функций.
Действительные числа. Приближение действительных чисел конечными десятичными дробями.
Погрешности приближений и вычислений. Практические приемы вычислений с приближенными данными.
Вычисления с помощью микрокалькуляторов. Вычисление значений выражений.
Дата: 2018-12-21, просмотров: 470.
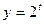 возрастает:
возрастает: