| – Я взяла 4 палочки-отрезка (учитель работает на фланелеграфе). Получился ли у меня квадрат? Почему? (Незамкнутая линия.) Я замкну линию. Как называется такая фигура? (Многоугольник.) | 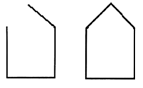
|
Вывод : замкнутая фигура, имеющая несколько углов и столько же сторон, называется многоугольником.
– Сегодня мы познакомимся с разными многоугольниками, узнаем, почему они так называются, от чего зависят их названия. Будем учиться их выкладывать из палочек и вычерчивать. Как вы понимаете слово «многоугольник»? (Много углов.)
– Я расскажу вам сейчас историю, которая произошла с нашими гостями – Треугольником и Квадратом.
| Жили-были два брата: Треугольник с Квадратом. Старший – квадратный, Добродушный, приятный. Младший – треугольный, Вечно недовольный. Стал расспрашивать Квадрат: «Почему ты злишься, брат?». Тот кричит ему: «Смотри, Ты полней меня и шире, У меня углов лишь три, У тебя же их четыре!». | Но Квадрат ответил: «Брат! Я же старший, я – Квадрат!». И сказал еще нежней: «Не известно, кто нужней!..» Вот настала ночь, и к брату, Натыкаясь на столы, Младший лезет воровато Срезать старшему углы. Уходя, сказал: «Приятных Я тебе желаю снов! Спать ложился – был квадратным, А проснешься без углов!..» |
– Что сделал младший брат? (Срезал углы.)
– У вас на столе лежат квадраты. Загните у них углы. Посчитайте, сколько углов получилось. (Восемь.) Послушайте, что было дальше.
| …Но наутро младший брат Страшной мести был не рад. Поглядел он – нет Квадрата! | Онемел, стоял без слов… Вот так месть! Теперь у брата Восемь новеньких углов. |
– Какое название можно дать этой фигуре? (Восьмиугольник.)
– От чего же зависит название многоугольника?
Вывод : название многоугольника зависит от количества углов.
– Выложите на парте многоугольники (два ученика работают на фланелеграфе): I вариант – пятиугольник; II вариант – шестиугольник.
– Сколько палочек-отрезков потребовалось? Почему?
Вывод : название многоугольника зависит и от количества сторон.
– Одинаково ли количество углов и сторон у каждого многоугольника? (Да.)
– Рассмотрите фигуры на доске.
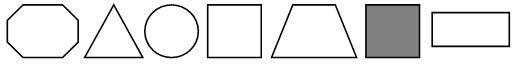
– Покажите четырехугольники; треугольники; восьмиугольники.
– Как одним словом назвать фигуры, которые вы показали? (Многоугольники.)
– Все ли здесь многоугольники? Покажите «лишнюю» фигуру. Почему?
На доске – геометрические фигуры.

– Как называются все эти фигуры? (Многоугольники.)
– А если я возьму два отрезка, получится ли многоугольник? (Нет.)
– Какое минимальное количество сторон и углов может быть у многоугольника? (Три.)
V. Самостоятельная работа (тест).
1. Сосчитайте число сторон и углов многоугольников и назовите их.
Обведите красным цветом пятиугольники, синим – четырехугольники, зеленым – семиугольники.
Как называется оставшийся многоугольник?
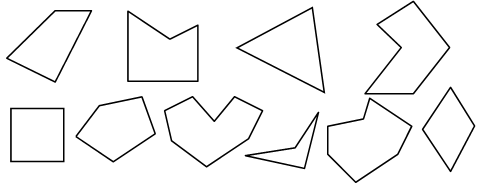
2. Посчитайте количество многоугольников на чертеже.
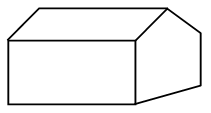
3. Графический диктант.
– Пишем: 8 кл. вверх, 4 кл. вправо вниз по диагонали, 4 кл. влево вниз по диагонали, 5 кл. вправо, 8 кл. вверх, 4 кл. вправо вниз по диагонали, 4 кл. влево вниз по диагонали, 6 кл. вправо, 3 кл. влево вниз по диагонали, 8 кл. влево, 3 кл. влево вверх по диагонали, 3 кл. вправо.
| – Какую фигуру напоминает корпус лодки? С какими фигурами познакомились? От чего зависит название многоугольников? Какое количество углов и сторон должно быть у каждого многоугольника? Какое минимальное количество сторон у многоугольников? | 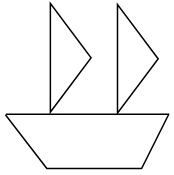
|
4. Кроссворд.
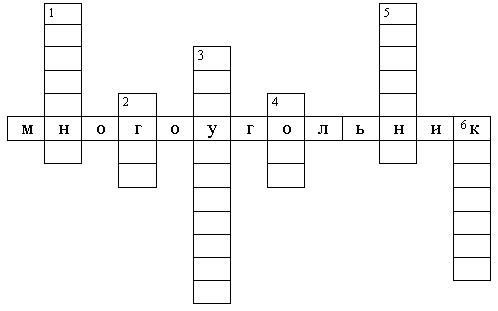
Задание: 1. Точка, из которой исходят лучи. 2. Уголь, но без ь. 3. Фигура, у которой 3 угла, 3 стороны, 3 вершины. 4. Фигура, у которой 4 стороны и противоположные углы равны. 5. Как называются лучи, образующие угол? 6. Фигура, у которой все стороны равны.
Ответы: 1. Вершина. 2. Угол. 3. Треугольник. 4. Ромб. 5. Стороны. 6. Квадрат.
VI. Итог урока.
– Какие фигуры называют четырехугольниками?
Урок 42
ТРЕУГОЛЬНИКИ
Цели деятельности учителя: познакомить с видами треугольников (прямоугольный, остроугольный, тупоугольный, равносторонний); содействовать развитию умения различать виды треугольников на чертеже, определять площадь фигур по клеткам, разрезать прямоугольник на два треугольника.
Планируемые результаты образования.
Предметные: умеют различать прямой, острый и тупой углы на рисунках, распознавать прямоугольный треугольник, определять площадь прямоугольника (в условных единицах с опорой на иллюстрации).
Личностные: оценивают собственные успехи в освоении вычислительных навыков; сопоставляют собственную оценку своей деятельности с оценкой её товарищами, учителем.
Метапредметные (критерии сформированности/оценки компонентов универсальных учебных действий – УУД): регулятивные: организуют взаимопроверку выполненной работы; планируют собственную вычислительную деятельность; познавательные: экспериментируют с треугольниками (количество прямых и тупых углов); выполняют вычисления по аналогии; вычисляют площадь многоугольной фигуры, разбивая ее на прямоугольники; конструируют фигуры из частей прямоугольника; коммуникативные: отвечают на вопросы, задают вопросы, уточняют непонятное.
Ход урока
Дата: 2018-12-21, просмотров: 416.