1. Посчитайте, сколько на рисунке прямоугольников и сколько квадратов. (Прямоугольников – 19, квадратов – 10.)

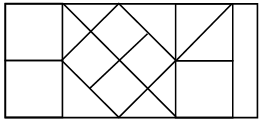
2. Сколько таких прямоугольников поместится в этом квадрате?

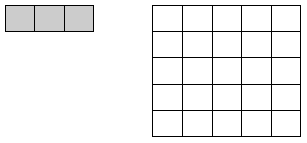
3. Сколько таких квадратов поместится в этом прямоугольнике?

II. Изучение нового материала.

Работа по учебнику.

– Сегодня мы применим наши знания по геометрии на практике и спроектируем парк Винни-Пуха.

Задание 1. С помощью линейки проведите по сторонам клеток в верхней части тетрадного листа прямую линию, как показано на рисунке. Это верхняя граница парка.

Задание 2. Слева проведите по сторонам клеток прямую сверху вниз.

Задание 3. От точки пересечения отложите по линейке вниз по прямой 6 см. Отметьте получившуюся точку и проведите через нее нижнюю границу парка.

Задание 4. По верхней (или нижней) прямой отметьте от точки пересечения прямых 8 см, поставьте точку. Через эту точку проведите сверху вниз ещё одну прямую.

Задание 5. Какие углы образовались при пересечении прямых? (Прямые углы.)

– Какую фигуру ограничивают проведенные прямые? (Прямоугольник.)

– Сотрите ластиком лишние линии так, чтобы получился прямоугольник.

Задание 6. С помощью линейки соедините противоположные вершины прямоугольника. Построенные отрезки называют диагоналями прямоугольника.

Задание 7. Поставьте в центре парка домик Винни-Пуха – нарисуйте точку. Обозначьте её буквой В.

– В левом верхнем углу обозначьте точкой К домик Кролика.

– В правом верхнем углу – домик Пятачка. В левом нижнем углу – домик Иа-Иа. А в правом нижнем углу – домик Совы.

– Измерьте расстояния между домиками. Расставьте эти числа на плане.

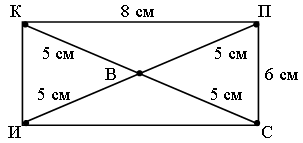
– Друзья любят ходить в гости. После завтрака Винни-Пух навестил Сову и потом зашел пообедать к Пятачку. После обеда друзья заглянули к Кролику и пришли поужинать к Винни-Пуху.

– Сколько прошёл Винни-Пух до обеда? А сколько после? (До обеда: 5 + 6 = 11; после обеда: 8 + 5 = 13.)

Задание 9. Какие углы образуют между собой тропинки между домиками?

а) КВ и ВП – тупой угол;      г) КИ и ИС – прямой угол;

б) ИВ и ВК – острый угол;  д) ИП и ПК – острый угол.

в) СП и ПК – прямой угол;

Задание 10. Обозначим маршруты прогулок буквами. Чтобы сообщить важное известие, Кролику нужно обежать всех жителей парка. Какой маршрут длиннее: КИСПВ или КИВПС? (Маршрут КИСПВ: 6 + 8 + + 6 + 5 = 25, маршрут КИВПС: 6 + 5 + 5 + 6 = 22.)

– Винни-Пух пришёл к Пятачку, и они решили навестить всех-всех-всех. Какой маршрут короче: ВПСИК или ВПСКИ? (Маршрут ВПСИК: 5 + 6 + 8 + 6 = 25, маршрут впски: 5 + 6 + 10 + 6 = 27.)

Задание 11. Раскрасьте парк. Придумайте еще задачи к этому рисунку и решите их.

III. Самостоятельная работа по карточкам.

1. Сколько нужно сделать распилов, чтобы распилить бревно на 4 части? Подчеркните правильный ответ: 2, 3, 4.

2. Нарисуйте пропущенные фигуры.

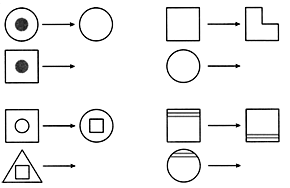
3. Вырежите из бумаги в клетку квадрат со стороной 3 см. Отрежьте все его углы. Посчитайте, сколько получилось углов. Подчеркните правильный ответ: 4, 6, 8.

4. Вычислите длину ломаной линии, если длина первого звена 6 см, а длина каждого следующего звена на 2 см больше предыдущего. Ломаная состоит из трех звеньев.

Урок 41
четырЁхугольники

Цели деятельности учителя : познакомить со свойствами сторон и углов четырёхугольников; способствовать развитию умения измерять диагонали прямоугольника, квадрата, ромба, выполнять построение фигур на клетчатой бумаге; содействовать закреплению умения сравнивать площади фигур и делить четырёхугольник на треугольники.

Планируемые результаты образования.

Предметные: умеют измерять длину заданного отрезка, чертить с помощью линейки отрезок заданной длин, определять площадь прямоугольника (в условных единицах с опорой на иллюстрации).

Личностные: проявляют положительное отношение и интерес к урокам математики; воспринимают математику как часть общечеловеческой культуры.

Метапредметные (критерии сформированности/оценки компонентов универсальных учебных действий – УУД): регулятивные: планируют собственные действия по устранению пробелов в знаниях (знание геометрических фигур); планируют собственную вычислительную деятельность; познавательные: исследуют простейшие свойства четырехугольников: измеряют стороны и диагонали, сравнивают, делают выводы, проверяют их на других фигурах, моделируют квадрат и ромб с помощью конструктора, экспериментируют с моделями, вычисляют площадь многоугольной фигуры, разбивая ее на прямоугольники; коммуникативные: высказывают своё мнение при обсуждении задания; при выполнении заданий в паре слушают друг друга, договариваются, объединяют полученные результаты при совместной презентации решения.

Ход урока