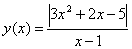.
Решение:
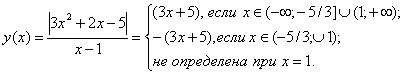
Отсюда график:
2. Решите в целых числах уравнение x²-3 xy+2 y²=7.
Решение: Разложим -3ху на два слагаемых –ху и -2ху. Тогда получим: х²-ху-2ху+2у²=7. Сгруппируем и вынесем за скобки (х-у) и получим: (х-у)(х-2у)=7. Учитывая, что 7=1·7=7·1=-1·(-7)=-7·(-1), получим следующие четыре системы уравнений:
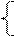
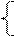
х-у=1, х-у=7, х-у=-1, х-у=-7,
х-2у=7, х-2у=1, х-2у=-7, х-2у=-1.
Решая данные системы, найдем решения уравнения: (-5;-6), (5;6), (13;6), (-13;-6).
Ответ: (-5;-6), (5;6), (13;6), (-13;-6).
3. Сторона ВС в ∆АВС на 2 см больше стороны АВ, а АС = 5 см, ∠ А = 2 ∠ C . Найти АВ и ВС.
Решение:
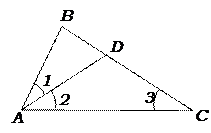Проведем биссектрису AD. Тогда ∠1 = ∠2 = ∠3. В DA D C AD = DC. Пусть АВ = х, AD = DC = y, тогда ВС = х + 2, BD = x + 2 – y. Заметим, что DAB D ~ DABC по двум углам (∠В – общий, ∠1 = ∠3).
Из подобия имеем: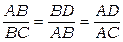 
, или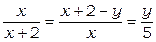 
.
Для нахождения х и у получим систему уравнений:
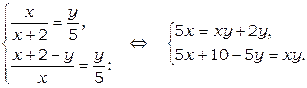
Вычитая из первого уравнения второе, получим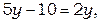 
откуда 
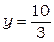, тогда 
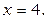значит АВ = 4см, ВС = 6см.
II способ. Указание: применить теорему синусов.
Ответ: AB = 4см, ВС = 6см.
Можно ли число 1234 представить в виде разности квадратов двух целых чисел?
Решение:
Допустим, что 1234= а2 -b2 , где а и b – целые числа. Тогда 1234 = (а+ b)(а- b).
Рассмотрим четыре случая: а) а – четное, b – четное; б) а - четное, b – нечетное; в) а – нечетное, b – четное; г) а – нечетное, b – нечетное.
В случаях б) и в) числа (а+ b) и (а- b) нечетны, значит, их произведение нечетно и не может равняться четному числу 1234.
В случаях а) и г) числа (а+ b) и (а- b) четны, значит, их произведение делится на 4 и не может равняться числу 1234, на 4 не делящемуся.
Следовательно, число 1234 нельзя представить в виде разности квадратов двух целых чисел.
Ответ: нельзя.
5. Двое по очереди закрашивают клетки таблицы 8 ´ 8. одним ходом разрешается закрасить одну или несколько клеток, расположенных либо в одной строке, либо в одном столбце таблицы. Клетки, закрашенные ранее, закрашивать вторично запрещается, проигравшим считается тот, кто не может сделать очередной ход. Кто выигрывает при правильной игре: начинающий или его партнёр?
Решение:
Для того чтобы победить, он должен каждым своим ходом закрашивать клетки, симметричные клеткам, закрашенным предыдущим ходом начинающего (относительно центра доски или одной из осей симметрии доски, параллельной её краям).
Ответ: выигрывает партнёр начинающего.
Всероссийская олимпиада школьников – 2018
Школьный этап
Математика
Класс
1. Решить в целых числах уравнение: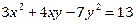 
.
Решение:
Разложением на множители получим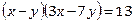 
, заметим, что в данном случае мы ничего не прибавляли к обеим частям уравнения. Так как число 13 – это 13⋅1, 1⋅13, −13⋅(−1), −1⋅(−13) ,
то мы получаем совокупность четырех систем:
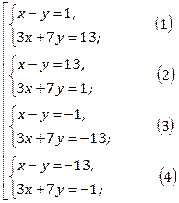
Решая системы выражением одной переменной через другую, получаем, что системы (2) и (4) решений в целых числах не имеют, а ответами систем (1) и (3) являются соответственно
x = 2, y = 1 и x = −2 , y = −1
Ответ: (2;1), (-2;-1).
2. Постройте график функции: у =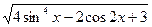 
+ 
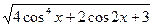
Решение :
y= +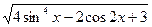
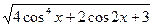
y=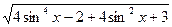 
+ 
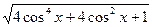
y=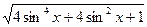 
+ 
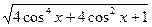
y= 2sin²x+1+2cos²x+1
y=4
Ответ: графиком функции является прямая, заданная уравнением у=4.
3. При каких значениях параметра m уравнение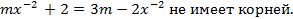 
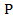ешение :
ОДЗ: х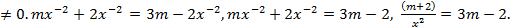 
1-й случай. Если 3m-2=0, то m =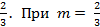 
имеем m + 2 = 
+2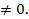 
В этом случае в левой части преобразованного уравнения будет выражение, отличное от нуля при любом х из ОДЗ уравнения, а в правой части – нуль. Следовательно, при m = 
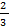данное уравнение решений не имеет, то есть m =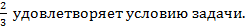 
2-й случай. 3m-2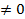 
. Тогда х2 = 
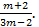Так как х≠0, то полученное уравнение не имеет решений тогда и только тогда, когда 
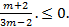Решая это неравенство, получим -2 
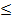m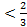 
.
Так как в первом случае показано, что m = , также удовлетворяет условию задачи, то получим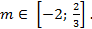 
Ответ: m∈ [-2; ].
Дата: 2018-11-18, просмотров: 328.
