Школьный этап
Математика
Класс
1. Допишите к числу 523 три цифры так, чтобы полученное шестизначное число делилось на 7, 8 и 9. Обоснуйте ответ.
Ответ. 523152, 523656.
Решение.
1) 7*8*9 = 504,
2) 523000=504*1037+352,
3) 504-352=152,
4) 523000+152=523152, 523152+504=523656, 523656+504>523000
2. Дана линейная функция у = kx +b. При каком значении b график этой функции проходит через точку пересечения графиков функций у= 1,2-х и у= х+4 и параллельно прямой у=-3х+5?
Ответ. -1,6.
Решение.
1,2-х=х+4, х=-1,4; у= 2,6, т.е. (-1,4; 2,6)- точка пересечения графиков у= 1,2-х и у= х+4;
т.к. прямые у = kx +b и у=-3х+5 параллельны, то k=-3;
2,6=-3 
(-1,4)+ b, отсюда b=-1,6.
3. От пластмассового равнобедренного треугольника отломились два угла при основании, от которого осталась одна точка (на рисунке это точка M). Как восстановить этот треугольник на бумаге?
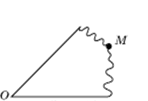
Решение.
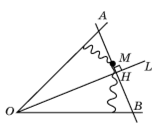Воспользуемся признаком равнобедренного треугольника. Обведем на бумаге контур оставшегося треугольника, проведем биссектрису OL данного угла O, проведем прямую MH перпендикулярно к OL (H 
OL); точки A и B – точки пересечения MH со сторонами данного угла O. Отрезок ОН является высотой и биссектрисой в 
AOB, значит, 
AOB – искомый равнобедренный треугольник.
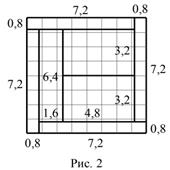
4. Разрежьте квадрат со стороной 8 см на семь прямоугольников, каждый из которых имеет периметр 16 см. Не забудьте указать размеры полученных прямоугольников.
Решение. Возможны два варианта.
| 
|
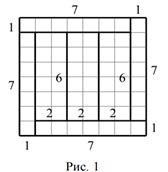
5. Задача Я. Перельмана.
Может ли алгебра понадобиться в парикмахерской? Оказывается, что такие случаи бывают.
Мне пришлось убедиться в этом, когда однажды в парикмахерской подошел ко мне мастер с неожиданной просьбой:
- Не поможете ли нам разрешить задачу, с которой мы никак не справимся?
- Уж сколько раствора испортили из-за этого! - добавил другой.
- В чем задача? - осведомился я.
- У нас имеется два раствора перекиси водорода: 30-процентный и 3-процентный. Нужно их смешать так, чтобы составился 12-процентный раствор. Не можем подыскать правильной пропорции…
Мне дали бумажку, и требуемая пропорция была найдена.
Она оказалась очень простой. Какой именно?
Ответ. 3-процентного раствора надо взять вдвое больше, чем 30-процентного.
Решение.
Пусть для составления 12-процентной смеси требуется взять х граммов 3-процентного раствора и у граммов 30-процентного. Тогда в первой порции содержится 0,03x граммов чистой перекиси водорода, во второй 0,3y, а всего 0,03x + 0,3y. В результате получается (х + у) граммов раствора, в котором чистой перекиси должно быть 0,12(х + у). Имеем уравнение 0,03x + 0,3y = 0,12(x + y).
Из этого уравнения находим х = 2у, т. е. 3-процентного раствора надо взять вдвое больше, чем 30-процентного.
Всероссийская олимпиада школьников – 2018
Школьный этап
Математика
Класс
1. Решите в натуральных числах:
.
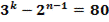Ответ: k = 4; n = 1.
Решение: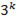 
- нечетно, то и 
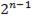нечетно. Это может случиться только тогда, когда 
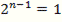⇒ n – 1 = 0 ⇒ n =1. 
⇒ 
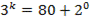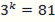; k = 4.
2. Решите уравнение:
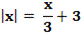
Ответ: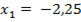 
; 
.
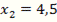Решение: 1 способ: 1 сл: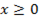 
;
;
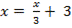3x < x + 9;
2x = 9;
x = 4,5 – удовлетворяет, т.к. x ≥ 0.
2 сл: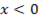 
;
;
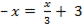– 3x = x + 9;
– 4x = 9;
x = -2, 25 – удовлетворяет, т.к. x < 0.
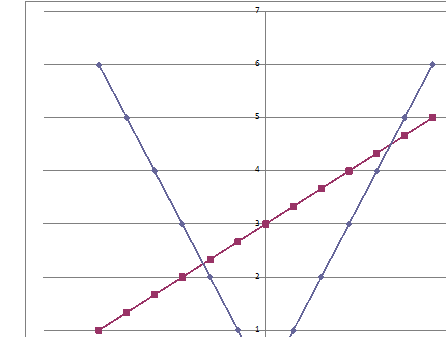
2 способ: Рассмотрим и построим графики функций:
.
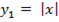
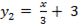3. В классе провели контрольную работу по математике. Средняя оценка мальчиков 3,8; девочек - 3,5; в классе -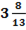 
Сколько человек писало контрольную работу, если их больше 20 и меньше 30?
Ответ: 26 учеников.
Решение: «М» - количество мальчиков и «Д» - количество девочек, то согласно условию задачи:
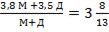; или 3,8 * 13 М + 3,5 * 13 Д = 47 М
М (3,8 * 13 - 47) = Д (47 – 3,5 * 13).
М =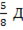 
;
Всего детей писавших контрольную работу: Д +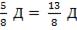 
; где 
целое число.
Пусть 
= k; то по условию 20 < 13 k < 30.
Значит, контрольную писали 26 учеников.
4. Внутри ΔABC взята точка K так, что ∠ ABK = 30˚, ∠ KAB = 10˚, ∠ ACB = 80˚ и AC = BC. Найти ∠ AKC.
Ответ: ∠ AKC = 70˚.
 |
|
|
|
|
|
|
|
| ||||
| ||||
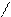
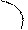
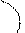
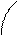
Пусть E — пересечения высоты CD и прямой BK. Так как Δ ABC — равнобедренный и CD — высота, проведенная к основанию AB, то AE = BE и
∠ EAK = ∠ EAB – ∠ KAB = 30˚ – 10˚ = 20˚ ,
∠ ACD = 
∠ ACB = 40˚,
∠ EAC = ∠ CAD – ∠ EAB = (90˚ – 40˚) – 30˚ = 20˚,
∠ AKE = ∠ KAB + ∠KBA = 10˚ + 30˚ = 40˚ ⇒ Δ AEK = Δ ACE (по стороне и прилежащим к ней углам) ⇒ AK = AC, ∠ AKC = ∠ ACK = 
(180˚ – ∠ CAK) = 
(180˚ – 40˚) = 70˚.
5. Двое играют в следующую игру: на столе лежит коробок спичек, и они по очереди берут оттуда спички. За один ход разрешается взять от одной до десяти спичек. Выиграет тот, кто заберёт последнюю спичку. Может ли начинающий выиграть при любой игре соперника, т.е. существует ли у него выигрышная стратегия, если вначале в коробке было 15 спичек? 50 спичек?
Ответ: 15 и 50 спичек. Выигрывает начинающий (первый ход соответственно 4 спички и 6 спичек).
Решение:
Случай 15 спичек. Начинающий выигрывает, взяв 4 спички. Остается 11спичек, сколько бы не взял соперник, начинающий может забрать оставшиеся.
Случай 50 спичек: Мы уже заметили, что после любого хода одного из игроков другой может взять несколько спичек так, что в сумме получится 11 спичек (если один берёт k спичек, то другой берёт «11-k», а из неравенства «1 ≤ k < 10» следует «1 ≤ 11-k ≤ 10»), поэтому начинающему следует взять несколько спичек так, чтобы в коробке осталось количество спичек кратно 11, то есть он должен взять 6 спичек. В коробке останется 44 спички. После ответа соперника надо оставить 3 спички, затем 22, 11 и, наконец, 0. То есть взять последние несколько спичек.
Следует заметить, что начинающему ни на что нельзя отступать от этой стратегии – иначе инициативу перехватит соперник, и выигрышная стратегия будет у него. Например, если начинающий первым ходом возьмёт не 6 спичек, а 5, что второй возьмёт 1 спичку и уже после его хода останется 44 спички. Если же начинающий возьмёт не 6 спичек, а 7, то второй возьмёт 10, и останется 33 спички.
Дата: 2018-11-18, просмотров: 316.
