Школьный этап
Математика
Класс
1. В шахматном турнире играли пять человек. Каждый из них сыграл с каждым по одному разу. Победитель партии получал 1 очко, проигравший – 0 очков, а если партия заканчивалась вничью, то каждый получал по 0,5 очка. Известно, что половина партий турнира закончилась вничью, а игрок, занявший последнее место, проиграл все партии. Какое место занял игрок, набравший 3 очка?
Ответ: первое место.
Решение Всего в этом турнире было сыграно 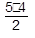 = 10 партий. Так как половина партий закончилась вничью, то результативных партий было пять. Четыре из них были сыграны с шахматистом, занявшим последнее место, то есть в партиях между остальными игроками была одержана только одна победа. Игрок, набравший три очка, должен был выиграть, по крайней мере, две партии, поэтому именно он заработал это очко. Любой из оставшихся шахматистов одержал не более одной победы, то есть набрал не более, чем 1 + 0,5 + 0,5 + 0,5 = 2,5 очка. Следовательно, игрок, набравший 3 очка, стал победителем турнира.
= 10 партий. Так как половина партий закончилась вничью, то результативных партий было пять. Четыре из них были сыграны с шахматистом, занявшим последнее место, то есть в партиях между остальными игроками была одержана только одна победа. Игрок, набравший три очка, должен был выиграть, по крайней мере, две партии, поэтому именно он заработал это очко. Любой из оставшихся шахматистов одержал не более одной победы, то есть набрал не более, чем 1 + 0,5 + 0,5 + 0,5 = 2,5 очка. Следовательно, игрок, набравший 3 очка, стал победителем турнира.
2. В озере водятся караси и окуни. Два рыбака поймали 70 рыб, причём 5/9 улова первого рыбака составляли караси, а 7/17 улова второго - окуни. Сколько рыб поймал каждый рыбак?
Решение. Количество рыб, пойманных вторым рыбаком, кратно 17, следовательно, оно может быть равно: 17, 34, 51 или 68. Количество рыб, пойманных первым, может равняться (соответственно) 53, 36, 19 или 2. Но количество рыб, пойманных первым, должно быть кратно 9, откуда получим ответ: первый рыбак поймал 36 рыб, второй - 34.
Заметим, что для данного решения несущественно, что в озере не водится иных рыб, кроме карасей и окуней.
Ответ. Улов 36 рыб и 34 рыбы.
3. В некотором натуральном числе цифры заменили буквами (одинаковые – одинаковыми, разные ‑ разными) и получили слово МАТЕМАТИКА. После этого стерли часть букв, а остальные переписали в обратном порядке. Получилось число 235405. Какое наибольшее число могло быть вначале?
Ответ. 9504950325.
4. На бильярдном столе лежат 15 шаров с номерами 1,2,3, … ,14,15. Как разложить их на шесть групп, чтобы сумма номеров шаров в каждой группе была квадратом натурального числа?
Решение: 1,3;4;2,14;5,11;6,10;7,8,9,12,13,15.
5. Три наследника разделили квадратный садовый участок со стороной 60 метров на три прямоугольные части равной площади. При этом каждые два наследника стали соседями. Какова общая длина забора, построенного внутри участка для отделения трех частей друг от друга?
Решение: Рассмотрим возможные способы разбиения квадрата на три прямоугольника. Один прямоугольник «отрезается» прямой, параллельной стороне квадрата, после чего есть ровно два способа разбиения одного из получившихся прямоугольников на два (см. рис. а), б).
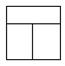 а) а)
|  б) б)
|
Второй способ разбиения квадрата (см. рис. б) не удовлетворяет условию, так как в этом случае два участка не имеют общей границы.
Для разбиения, показанного на рис. а), найдем общую длину границы между участками. Площадь садового участка равна 602 = 3600 (м2), поэтому каждому наследнику достался прямоугольный участок площадью 1200 м2. Ширина каждого из прямоугольников, расположенных на рис. 2а вертикально, равна половине стороны квадрата, то есть 30 м, поэтому их высота равна
1200 : 30 = 40 (м). Следовательно, длина внутреннего забора равна
40 + 60 = 100 (м).
Ответ: 100 метров
Дата: 2018-11-18, просмотров: 345.