ВВЕДЕНИЕ
Дисциплины «Химия кремния» и «Физическая химия силикатов» являются базовыми для технологических дисциплин, охватывающими такие вопросы, как учение о фазовых равновесиях поликомпонентных систем, строении и свойств силикатных материалов при различных температурах, термодинамику силикатов, структурно-механические и реологические свойства силикатных суспензий и расплавов, процессы спекания керамических масс, взаимодействие силикатов в твердом состоянии.
Силикатная промышленность является одной из наиболее старых, ее изделия датируются вторым тысячелетием до нашей эры. Романцемент использовался в Римской империи в период ее расцвета для возведения грандиозных сооружений.
Необходимость научного обоснования процессов, происходящих с исходным сырьем в процессе обжига, направленного формирования структуры строительных силикатных материалов, проектирования новых материалов и эффективных технологий их изготовления, в том числе при использовании техногенных отходов промышленности – все это явилось причиной выделения физической химии силикатов в самостоятельную дисциплину.
В настоящее время использование современных научных знаний позволяет получать высококачественные материалы со специальными свойствами, используемыми как в строительстве, так и в других отраслях, промышленности: металлокерамика, специальное стекло и ситаллы, оптическое волокно и др.
Пособие имеет целью развитие у студента интереса к изучаемой дисциплине, практической отработке вопросов теоретического курса по решению задач, связанных с фазовым равновесием одно-, двух- и трехкомпонентных систем в порядке возрастания их сложности.
Самостоятельная проработка предлагаемых задач позволит студенту научно обосновать выбор параметров технологических процессов производства силикатных материалов, изучаемых на старших курсах.
Таблица 1
Кварцсодержащая порода
Значения коэффициентов
ДИАГРАММЫ РАВНОВЕСИЯ ДВУХКОМПОНЕНТНЫХ СИСТЕМ
Силикаты щелочных металлов
3.3.1. Система Na2O – SiO2
Диаграмма Na2O – SiO2 (рис. 5) имеет в своем составе следующие химические соединения.
Ортосиликат натрия 2Na2O∙SiO2: Na2[SiO4]. Доля оксида натрия в составе соединения составляет 68,1 %.
Метасиликат натрия Na2O∙SiO2: Na2[SiO4]. Доля оксида натрия в составе соединения составляет 50,8 %.
Дисиликат натрия Na2O∙2SiO2. Доля оксида натрия в составе соединения составляет 34,0 %.
Эвтектика с минимальной температурой плавления 793 °С по мере увеличения доли кремнезема в исходном составе возрастает.
Составы, содержащие от 20 до 50 % оксида натрия, полностью переходят в расплав в интервале температур 790 – 1200 °С.
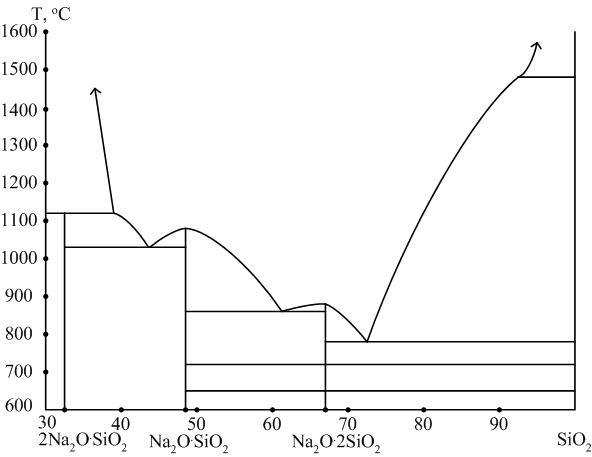
Рис. 5. Диаграмма Na2O – SiO2
Силикаты натрия растворимы в воде и используются для производства натриевого растворимого стекла состава Na2O∙nSiO2, где n – силикатный модуль стекла, изменяющийся от единицы до 4.
Растворимость силикатов натрия увеличивается со снижением силикатного модуля.
Жидкое стекло получают растворением силикат-глыбы, как правило, при избыточном давлении в автоклаве. Жидкое стекло обладает вяжущими свойствами и используется при изготовлении бумажных, деревянных и силикатных материалов, конструкций и изделий как вяжущее в кислотоупорных композициях, как средство для химического закрепления грунтов.
Задача № 32. Для системы Na2O – SiO2 определить максимальную температуру термообработки исходного сырья (сульфат натрия и кварцевый песок) для получения стекол с силикатным модулем 2,2.
Задача № 33. Для системы Na2O – SiO2 рассчитать состав шихты (исходное сырье карбонат натрия и кварцевый песок, содержащий 8 % органических примесей) для получения в системе при температуре 1000 °С расплава, содержащего 56 % SiO2.
Задача № 34. Известно, что в системе Na2O – SiO2 при температуре 1020 °С в равновесии с кристаллической фазой находится 40 % расплава. Определите все возможные для этих условий точки исходных составов и поясните, для какой из них растворимость силикат-глыбы будет выше.
Задача № 35. Рассматриваемый состав системы Na2O – SiO2, находящейся в равновесии, характеризуется следующими термодинамическими параметрами: температура 950 °С, количество расплава 30 %. Каким образом (не изменяя температуры) можно увеличить количество расплава до 50 %?
Задача № 36. Определить фазовый состав силиката (90 % SiO2 и 10 % Na2O) при температурах 1000 °С и 700 °С.
3.3.2. Система K2О – SiО2
В системе существует четыре химических соединения (рис. 6).
Ортосиликат калия 2K2О∙SiО2: K2[SiО4].
Доля оксида калия в составе силиката составляет 75,8 %. Соединение плавится конгруэнтно при температуре 513 °С, хорошо растворяется в воде. На диаграмме (рис. 6) соединение не показано.
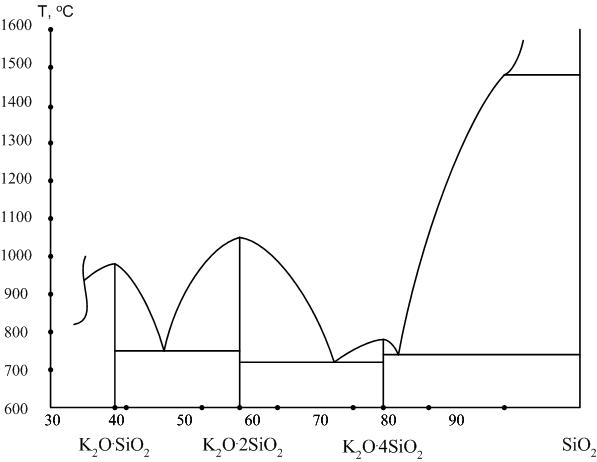
Рис. 6. Диаграмма K2О – SiО2
Метасиликат калия K2О∙SiО2: K2[SiО3].
Доля оксида калия в составе силиката составляет 61,0 %. Кристаллическая фаза гигроскопична, на воздухе кристаллы метасиликата легко растворяются парами воды.
Дисиликат натрия K2О∙2SiО2 и тетрасиликат калия K2О∙4SiО2, доля оксида калия в которых соответственно составляет 43,9 и 28,1 %.
Калиевые растворимые стекла по своим свойствам сходны с натриевыми, но в воде растворяются лучше последних.
Задача № 37. Определить, до каких температур следует нагреть исходные составы системы Na2O – SiO2 и K2О – SiО2 (доля SiO2 в составах 43 %), чтобы в равновесии с кристаллической фазой находилось 50 % расплава.
Задача № 38. Проведите анализ максимальной температуры обработки калиевых и натриевых силикатов одинакового состава с силикатным модулем 2 и 4 для получения в результате термообработки 80 % расплава. В каком случае энергозатраты будут выше?
Силикаты других металлов
3.4.1. Система MgO – SiO2
Интерес к изучению силикатов магния определяется их использованием в технологии производства магнезиальных огнеупоров и магнезиальных керамических материалов. Диаграмма системы MgO – SiO2 приведена на рис. 7.
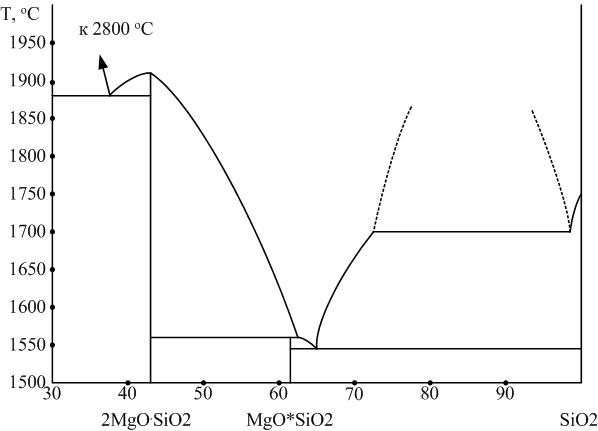
Рис. 7. Диаграмма двухкомпонентной системы MgO – SiО2
Ортосиликат магния 2MgO∙SiO2: Mg2[SiO4].
Природный аналог этого химического соединения носит название форстерит. Ортосиликат магния имеет высокую (1860...1890 °С) температуру плавления. В природе и в технических продуктах встречается главным образом в виде твердых растворов с фаялитом, называемых оливинами.
Метасиликат магния MgO∙SiO2: Mg[SiO3].
Плавится инконгруэнтно при температуре 1557 °С. Имеет несколько полиморфных модификаций, области фазовых равновесий которых и схемы полиморфных превращений которых на сегодня окончательно не установлены. Устойчивой при высоких температурах считается α-Mg[SiO3] – клиноэнстатит.
Диаграмма MgO – SiO2 интересна тем, что имеет высокую тугоплавкость бинарных составов. Даже эвтектические составы имеют температуру плавления не ниже 1543 °С.
Задача № 39. Для силиката магния, содержащего в своем составе 50 % SiO2, определить температуру, при которой степень спекания (массовая доля расплава в системе) достигает 30 %.
Задача № 40. Предложите параметры технологического процесса производства магнезиальных огнеупоров (исходные составы), для которых в процессе обжига при температуре 1860 оС образуется от 7 до 10 % расплава.
Задача № 41. Снизится ли огнеупорность силиката магния, нагретого до температуры 1700 °С, если в исходном составе доля кремнезема возрастет с 40 до 45 %?
Задача № 42. Можно ли магнезиальные огнеупоры использовать для футеровки стекловаренных печей (температура обработки не выше 1600 °С).
3.4.2. Система FeO – SiO2
Данная система играет важную роль в технологии силикатов.
Ортосиликат железа 2FeO∙SIO2: Fe2[SiO4].
Природный аналог этого химического соединения носит название фаялит. Ортосиликат железа плавится при температуре 1205 °С и при этом в расплаве образуется 2,25 % Fe2O3 и выделяется металлическое железо. Поэтому фаялит, несмотря на наличие максимума на кривой ликвидуса, относится к инконгруэнтно плавящимся соединениям. Фаялит образуется в богатых железом сварочных шлаках, в керамических изделиях в местах с повышенным содержанием в них железа.
В богатой кремнеземом части диаграммы наблюдается широкая область ликвации. При температуре 1698 °С одна жидкость содержит 97 %. другая – 60 % SiO2. Благодаря ликвации линия ликвидуса идет круто, а возникающее при введении добавки FeO к кремнезему количество жидкой фазы растет очень медленно с повышением температуры. Это позволяет применять в производстве динаса железистые минерализаторы и использовать такие огнеупоры в мартеновских печах без снижения их огневых свойств.
Задача № 43. Определить исходные составы в системе FeO – SiO2, для которых в продуктах кристаллизации находится 40 % фаялита. Для какого из этих составов кристаллизация начнется при более низкой температуре?
Задача № 44. Опишите процесс фазовых превращений в системе FeO – SiO2. (с изображением кривой охлаждения) исходного состава, для которого при некоторой температуре в равновесии в соотношении 3:2 находятся α-тридимит и расплав, содержащий 61 % SiO2.
Задача № 45. Определить объем, который при температуре 1730 °С будет занимать исходный состав системы массой 1 кг, содержащий 75 % SiO2, если плотности компонентов при этом будут составлять для SiO2 2,21 г/см3 и для FeO – 4,2 г/см3.
Задача № 46. Сравнить скорость нарастания количества жидкой фазы в системе FeO – SiO2 для исходных составов, содержащих 52 и 85 % SiO2 соответственно в температурном интервале от 1200 до 1350 °С.
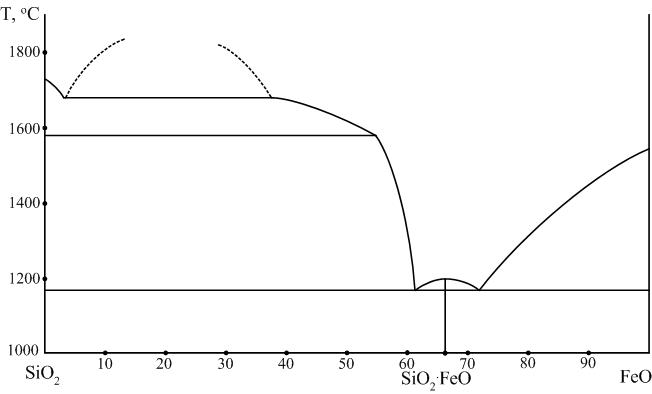
Рис. 8. Диаграмма двухкомпонентной системы FeO – SiO2
Задача № 47. Определить фазовый состав силиката (60 % SiO2, 40 % FeO) при температурах 1600 °С и 1300 °С.
3.4.3. Система PbO – SiO2
Диаграмма равновесия PbO – SiO2 представлена на рис. 9. Система является важной составной частью стекол и глазурей, содержащих свинец.
Тетрасиликат свинца 4PbO∙SiО2 среди других силикатов свинца обладает наибольшим светопреломлением (табл.2).
Таблица 2
Силикат свинца
Показатель светопреломления
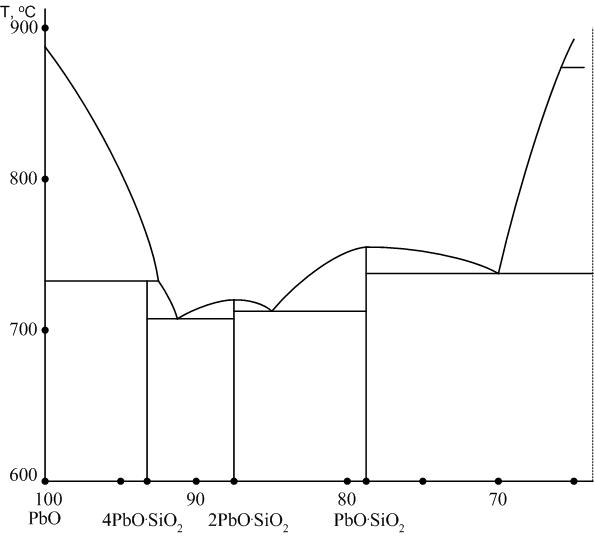
Рис. 9. Диаграмма двухкомпонентной системы PbO – SiO2
Именно по этой причине при производстве высококачественного хрусталя указывается молярный процент содержания оксида свинца в составе стекла (для хрусталя фирмы BOGEMIA молярная доля свинца достигает 32 %).
Задача № 48. Определить, какое количество тетрасиликата свинца получится в системе PbO – SiО2 при охлаждении исходного состава, содержащего 7 % по массе SiO2, до температуры 710 °С.
Ортосиликат свинца 2PbO∙SiО2 можно подучить кристаллизацией из расплава и при длительном отжиге свинцовых стекол.
Метасиликат свинца PbO∙SiО2 кристаллизуется из расплавов и при расстекловывании (кристаллизации) стекол.
Задача № 49. Определить исходный состав в системе PbO – SiО2, если известно, что в продуктах кристаллизации обнаружено 35 % кристаллов, имеющих показатель светопреломления 2,18.
Пример решения задач с использованием правила рычага
В трехкомпонентных системах
В решение задачи в обязательном порядке должно входить описание пути кристаллизации исходного или найденного в ходе решения задачи состава.
Задача №50. В системе A – В – C (рис. 10) в данный момент кристаллизации из расплава, количество которого составляет 30%, выделяются кристаллы АС и С в соотношении 1:3, а твердая фаза, выделившаяся к этому моменту за весь период, состоит из 28 %. кристаллов АС и 72 % кристаллов С. Определить исходный состав расплава и температуру, соответствующую данному моменту кристаллизации.
Решение
1. Совместно кристаллы АС и С могут выделяться только на конгруэнтной пограничной кривой G2E, следовательно точка состава расплава принадлежит данной кривой. Соотношение выделяющихся при данной температуре твердых фаз соответствует отрезкам, на которые делит соединительную прямую АС – С касательная, проведенная к пограничной кривой G2E.
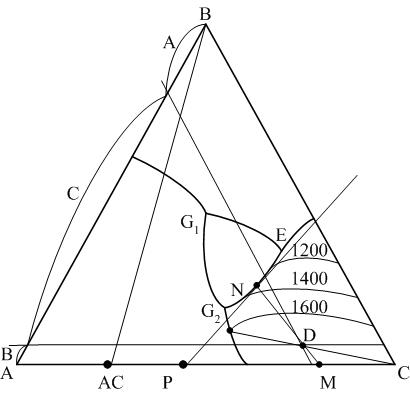
Рис. 10. Диаграмма состояния трехкомпонентной системы с двойным химическим соединение, разлагающимся в твердой фазе
Точка, в которой одновременно кристаллизующиеся фазы АС и С соотносятся как 1:3, это точка Р на соединительной линии АС – С (отрезок АС – Р – (1 часть) определяет количество кристаллов АС, отрезок Р – С – (3 части) определяет количество кристаллов АС). Из полученной точки Р проводим касательную РN к пограничной кривой G2E и находим точку состава расплава и температуру, соответствующую данному моменту кристаллизации. С учетом интерполяции температура точки N соответствует 1360 оС.
2. Точка исходного состава определяется из следующих соображений. Если из точки состава расплава при температуре 1360 °С (точка N) провести прямую через точку исходного (искомого) расплава, то эта прямая должна разделить соединительную линию АС – С в соотношении 28:72. Это точка М. Следовательно, точка исходного состава находится на прямой МN и делит эту прямую на отрезки, находящиеся в соотношении 30:70 (равновесное количество расплава и твердой фазы). Этому условию соответствует точка D, состав которой 20 % компонента А, 8 % компонента В, 72 % компонента С.
Ответ. Исходный расплав имеет следующий состав: 20 % компонента А, 8 % компонента В и 72 % компонента С, температура, соответствующая данному моменту кристаллизации – 1360 °С.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Физическая химия силикатов: Учебник для студентов вузов/ А.А. Пащенко, А.А. Мясников, Е.А. Мясникова и др. ; Под ред. А.А. Пащенко. – М.: Высшая школа, 1986. – 368 с.
2. Горбунов С.П. Физическая химия силикатов: Текст лекций. – Челябинск: ЧГТУ, 1996. –95 с.
З. Куколев Г.В.Химия кремния и физическая химия силикатов. –М.: Высшая школа, 1966. – 455 с.
4. Сборник вопросов и задач по физической химии для самостоятельного контроля: Учебное пособие для вузов/ А. Г. Атанасянц, С.Ф. Блевский, Г.С. Каретников и др.; Под ред. С.Ф. Блевского. – М.: Высшая школа, 1979. – 119 с.
ПРИЛОЖЕНИЯ

ВВЕДЕНИЕ
Дисциплины «Химия кремния» и «Физическая химия силикатов» являются базовыми для технологических дисциплин, охватывающими такие вопросы, как учение о фазовых равновесиях поликомпонентных систем, строении и свойств силикатных материалов при различных температурах, термодинамику силикатов, структурно-механические и реологические свойства силикатных суспензий и расплавов, процессы спекания керамических масс, взаимодействие силикатов в твердом состоянии.
Силикатная промышленность является одной из наиболее старых, ее изделия датируются вторым тысячелетием до нашей эры. Романцемент использовался в Римской империи в период ее расцвета для возведения грандиозных сооружений.
Необходимость научного обоснования процессов, происходящих с исходным сырьем в процессе обжига, направленного формирования структуры строительных силикатных материалов, проектирования новых материалов и эффективных технологий их изготовления, в том числе при использовании техногенных отходов промышленности – все это явилось причиной выделения физической химии силикатов в самостоятельную дисциплину.
В настоящее время использование современных научных знаний позволяет получать высококачественные материалы со специальными свойствами, используемыми как в строительстве, так и в других отраслях, промышленности: металлокерамика, специальное стекло и ситаллы, оптическое волокно и др.
Пособие имеет целью развитие у студента интереса к изучаемой дисциплине, практической отработке вопросов теоретического курса по решению задач, связанных с фазовым равновесием одно-, двух- и трехкомпонентных систем в порядке возрастания их сложности.
Самостоятельная проработка предлагаемых задач позволит студенту научно обосновать выбор параметров технологических процессов производства силикатных материалов, изучаемых на старших курсах.
ОБЩИЕ СВЕДЕНИЯ О ДИАГРАММАХ СОСТОЯНИЯ
Диаграмма состояния представляет собой графическое изображение возможных равновесных состояний системы при различных условиях.
В основу построения диаграмм состояния положены принципы, сформулированные Н.С. Курнаковым.
1. Принцип непрерывности: при неизменном фазовом состоянии системы непрерывное изменение состава и внешних условий приводит к непрерывному изменению свойств отдельных фаз и системы в целом. Скачкообразное изменение свойств фаз и системы в целом является индикатором фазовых превращений.
2. Принцип соответствия: каждому равновесному состоянию системы соответствуют определенные геометрические образы на диаграмме.
Изменения, происходящие в системе, следует рассматривать как цепь последовательных равновесных состояний при бесконечно малом изменении термодинамических параметров (в реальных силикатных системах такими параметрами чаще всего выступают температура и концентрация компонентов системы).
Диаграммы состояния являются тем инструментом исследования для ученого и технолога, с помощью которого можно решать комплекс задач практического и теоретического характера.
Например, читателю хорошо известно из курса "Строительные, материалы", что свойства керамического черепка зависят от степени спекания сырца, то есть от доли расплава в объеме изделия. Назначение температуры обжига керамических изделий в зависимости от состава сырья для их производства – типичная технологическая задача, легко решаемая по соответствующим диаграммам.
Какие же задачи можно решать с помощью диаграмм? К часто встречающимся на практике можно отнести следующие:
· определение температуры начала и завершения в рассматриваемой системе при любом соотношении компонентов различных процессов: плавления, кристаллизации, изменения составов расплава и твердых растворов и т.п.;
· определение минералогического и химического составов равновесных фаз;
· расчет количественного соотношения равновесных фаз;
· определение степени достижения равновесного состояния системы.
Широкие возможности, которые дают диаграммы состояния как инструмента исследования, лежат в основе объяснения и усовершенствования процессов, протекающих при синтезе различных минералов и материалов. Диаграммы помогают устанавливать и объяснять влияние фазового состава конечного продукта технологического процесса на его свойства, что позволяет решать задачи оптимизационного характера при производстве обжиговых строительных материалов.
В изучаемом Вами пособии будут рассматриваться, в основном, диаграммы силикатных систем, то есть систем, одним из компонентов которых является кремнезем – SiO 2. При этом исходные сырьевые смеси в процессе переработки подвергаются действию высоких температур.
Общие положения диаграмм состояния применимы и для анализа, например, продуктов гидратационных процессов минералов портландцементного клинкера и иных гидравлически активных веществ.
Итак, приступим к рассмотрению диаграмм состояния общего вида. Естественно, что наиболее простыми диаграммами являются те, количество компонентов которых минимально, то есть диаграммы состояния однокомпонентных систем. Если вспомнить правило Гиббса, то для однокомпонентных неконденсированных систем, находящихся в равновесии, максимальное количество степеней свободы
Fmax=K – Pmin + 2.
Таким образом, существует всего два независимых термодинамических параметра, изменения значений которых не приведет к изменению количества равновесных фаз. Для однокомпонентной системы такими параметрами являются температура системы и давление паров над поверхностью жидкой фазы.
Именно по этой причине диаграммы однокомпонентных систем называют Т (температура) – Р(давление)-диаграммами.
Дата: 2018-11-18, просмотров: 755.