В основе инерциальной навигации лежат следующие законы классической механики.

Первый закон Ньютона (закон инерции). Материальная точка, на которую не действуют никакие силы, имеет постоянную по модулю и направлению скорость. Всякая свободная материальная точка совершает простейшее «инерциальное» движение, т. е. движется прямолинейно и равномерно ( 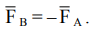= const) или находится в покое ( 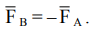= 0).

Второй закон Ньютона (основной закон динамики). Производная по времени от количества движения материальной точки равна действующей на неѐ силе, т. е.

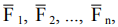                                        (5.1)

Поскольку, d( 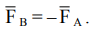)/dt = 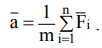, где 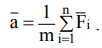 – ускорение точки, то при m = const

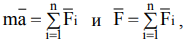                                             (5.2)

Третий закон Ньютона (закон действия и противодействия). Две материальные точки A и B двух тел действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны. Таким образом 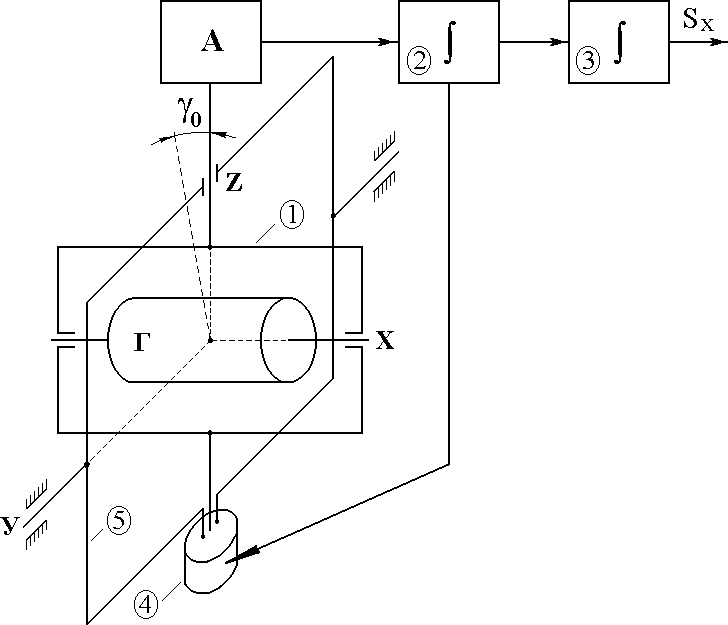                                               (5.3)

Этот закон предполагает дальнодействие, т. е. возможность действия материальных тел друг на друга на расстоянии, что характерно для классической механики Ньютона.

Закон независимости действия сил. Если на материальную точку действуют одновременно несколько сил, то каждая из этих сил действует независимо от других и сообщает точке ускорение, равное этой силе, делѐнной на массу точки. Следовательно, если на точку с массой m действует система сил , то ускорение, получаемое точкой,                                              (5.4)

Из формулы (5.4) следует, что , т. е. система нескольких сил F1, F2, ..., Fn действует на материальную точку так же, как одна сила F, равная сумме F1, F2, ..., Fn. Это следствие представляет обобщѐнный закон параллелограмма сил.

Всякое движение материального тела в пространстве является по своему существу относительным и требует обязательного указания системы отсчѐта (системы координат), по отношению к которой оно рассматривается. Сформулированные выше законы механики Ньютона справедливы только по отношению к некоторой определѐнной системе отсчѐта, которая называется «абсолютной» или «инерциальной».

Происхождение термина «инерциальный» связано с тем, что только в инерциальных системах координат справедлив первый закон Ньютона. Отсюда произошло и название «инерциальные системы координат», так как только в них справедлив закон инерции. Если наряду с инерциальной системой отсчѐта ввести другую систему, движущуюся относительно первой прямолинейно и равномерно, то законы механики по отношению к этой новой системе будут теми же, что и по отношению к первоначальной.

Физические принципы, лежащие в основе инерциальной навигации, неразрывно связаны с решением второй (основной) задачи динамики: зная действующие на тело силы, а также его начальное положение и скорость, определить закон движения тела, т. е. его положение в любой момент времени относительно выбранной системы отсчѐта.

В системе полуаналитического типа акселерометр жѐстко связан со стабилизатором и удерживается в горизонтальной плоскости. На рис. 5.7 показан гиростабилизатор, управляемый сигналами, пропорциональными интегралу по времени от измеренных ускорений.

Рис. 5.7. Полуаналитическая ИНС

Акселерометр A укреплѐн на внутренней раме 1 гироскопа Г. Сигнал акселерометра, после интегрирования первым интегратором 2, подаѐтся на двигатель 4. Статор двигателя 4 жѐстко укреплѐн на наружной раме 5 под- веса гироскопа, а ротор связан с осью вращения рамы 1. Момент этого двигателя, работающего в заторможенном режиме, вызывает скорость прецессии гироскопа вокруг горизонтальной оси У. С выхода второго ин- тегратора 3 получают расстояние S_x, пройденное в направлении оси Х.