 Рис. 3.25. Диаграммы направленности антенн наземного радиомаяка:
Рис. 3.25. Диаграммы направленности антенн наземного радиомаяка:
fон(j)–ДН остронаправленной антенны; fна(j) –ДН ненаправленной антенны
Датчики опорных импульсов установлены таким образом, чтобы в момент совмещения оси симметрии диаграммы направленности вращающейся антенны с северным направлением меридиана происходило совпадение одного из импульсов серии «35» с одним из импульсов серии «36». Это совпадение называют северным и используют в качестве сигнала начала отчёта времени при измерении азимута A. Для повышения точности фиксации момента прохождения оси симметрии диаграммы направленности вращающейся антенны через точку, где находится самолёт, используют двухлепестковую диаграмму направленности
 Рис. 3.26. Упрощённая функциональная схема угломерного канала РСБН:
Рис. 3.26. Упрощённая функциональная схема угломерного канала РСБН:
1) приёмник; 2,3) каналы выделения опорных импульсов;4) каскад совпадения; 5) канал выделения азимутального сигнала;6) измеритель временной задержки; 7) индикатор азимута

Рис. 3.27. Временные диаграммы сигналов на выходе самолётного
приёмника РСБН: «35» и «36» –опорные импульсы; «АС» –азимутальный сигнал
29.Доплеровские измерители скорости и угла сноса. Методы построения, функциональные схемы, основные уравнения.
Изменение частоты тем больше, чем больше скорость движения приёмника относительно передатчика. Такой же эффект имеет место, если передатчик и приёмник неподвижны относительно друг друга и находятся на движущемся объекте, а колебания принимаются после отражения от неподвижного объекта.
На летательном аппарате находится (РЛС), передатчик которой вырабатывает немодулированные колебания U1 = U1msinw1t = U1msinj1. (3.69)
Излучаемые колебания отражаются от точечного объекта на поверхности Земли, тогда принимаемые колебания будут U2 = U2msinw1(t – tд) = U2msinj2, (3.70)
здесь Д – расстояние от самолёта до точки отражения; tд = 2Д/C. (3.71)
Частота принимаемых колебаний определяется из выражения (3.70)
дифференцированием фазы w2 = dj2/dt = w1(1 – dtд/dt). (3.72)
Получим w2 = w1(1 – 2·Vд /C), (3.73)
Vд = dД/dt – радиальная скорость, т. е. скорость изменения расстояния в направлении распространения радиоволн.
Из уравнения (3.73) видно, что отражённые колебания отличаются по
частоте от излучаемых колебаний на величину WД
WД = w1(2·Vд /C), (3.74)-доплеровским смещением частоты (доплеровской частотой).
При приближении РЛС к точечному объекту на поверхности Земли
WД > 0, при удалении WД < 0, при неизменном расстоянии WД = 0.
Доплеровскую частоту можно выразить как FД = f1(2·Vд /C) = 2·Vд /l1. (3.75)
Выражение (3.75) показывает связь между доплеровской частотой и радиальной скоростью, последнюю можно связать с вектором путевой скорости W и углом сноса самолёта УС.
Углы  и υ называют установочными
и υ называют установочными
а) проекция на вертикальную плоскость; б) проекция на плоскость горизонта; V вектор истинной воздушной скорости; U вектор скорости ветра.
Vд = W·cos υ ·cos(  – УС). (3.76)
– УС). (3.76)
Подставляя (3.76) в (3.75), получим основное уравнение ДИСС:
W = {  1/[2cos υ ·cos(
1/[2cos υ ·cos(  – УС)]}·FД = MW ·FД, (3.77)
– УС)]}·FД = MW ·FД, (3.77)
здесь MW = 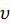 1/[2cos υ ·cos(
1/[2cos υ ·cos(  – УС)] – масштабный коэффициент.
– УС)] – масштабный коэффициент.
Рис. 3.30. Зависимость доплеровского сдвига частот от угла поворота антенны
При методе максимума антенна, снабжѐнная поворотным устройством, устанавливается так, чтобы измеритель частоты, включѐнный на выходе приѐмника, давал максимальные показания. При этом угол поворота антенны  равен углу сноса УС.
равен углу сноса УС.
При методе максимума антенна, снабжѐнная поворотным устрой-ством, устанавливается так, чтобы измеритель частоты, включѐнный на выходе приѐмника, давал максимальные показания. При этом угол поворота антенны  равен углу сноса УС.
равен углу сноса УС.
Метод сравнения не требует подвижных антенн и позволяет автоматически и одновременно измерять путевую скорость и угол сноса с приемлемой точностью. Для его реализации необходимы две антенны и два приѐмника. Можно использовать один приѐмник, который поочерѐдно подключается то к одной, то к другой антенне.
3.31. К построению ДИСС методом сравнения
Доплеровские частоты для колебаний, принятых первой и второй ан-теннами, соответственно равны:
FД 1 = [2cos 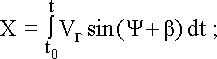 ·cos( ·cos( 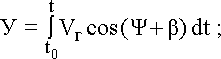 – УС)/ – УС)/ 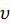 1]·W, 1]·W,
| (3.78) |
FД 2 = [2cos 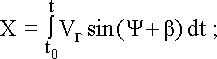 ·cos( ·cos( 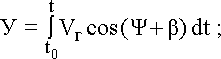 + УС)/ + УС)/ 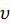 1]·W. 1]·W.
| (3.79) |
Уравнения (3.78, 3.79) получены независимыми путями и могут быть использованы для вычисления как W, так и УС. Приведѐнная выше теория ДИСС справедлива только при горизонтальном полѐте. Если имеется крен или тангаж, то точность ДИСС уменьшается.
Дата: 2018-09-13, просмотров: 841.