Основная методическая погрешность навигационного автомата счисления пути, основанного на интегрировании скорости относительно воздуха, вызывается отсутствием точной и непрерывной информации на летательном аппарате о скорости ветра. Кроме этого, существуют методические погрешности, вызванные погрешностями датчиков истинной воздушной скорости и курса.

Уравнения в общей форме Х = F₁(V, Y, U, d),  У = F₂(V, Y, U, d), (4.16)

где Х, У – координаты места, то методические погрешности можно определить в линейном приближении путѐм разложения в ряд:

– здесь DU, DY, DV, Dd - первичные погрешности в измерении истинной воздушной скорости, истинного курса, скорости и направления ветра.

Погрешности, вызванные неполным учѐтом параметров ветра

Предположим, что каким-либо средством навигации получены сведения о скорости U₀ и направлении d₀ ветра. Фактические значения скорости и направления ветра U и d. Используя уравнения (4.17, 4.18), найдѐм погрешности в определении координат, вызванные погрешностями в определении скорости DU = U – U0 и направления ветра Dd= d–d₀.

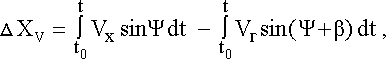
	(4.19)
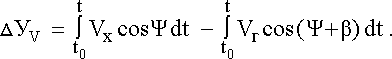
	(4.20)

Значение DU может достигать десятков км/час, а угол Dd – единиц градусов (2-3С°). Частота введения поправок на ветер определяется следующим образом. Задаются допустимыми погрешностями измерения координат DS и предполагаемым средним значением скорости ветра DUср, которую не учитывает навигационный автомат. Допустимый интервал времени DTдоп между двумя коррекциями определится как:

DT_доп = DS/DU_ср. (4.21)

Погрешности навигационных автоматов, вызванные погрешностями определения вектора истинной воздушной скорости

Вектор истинной воздушной скорости V не совпадает с продольной осью летательного аппарата. Наличие углов атаки a, скольжения b приводит к тому, что фактическое движение в горизонтальной плоскости относительно воздуха определяется уравнениями

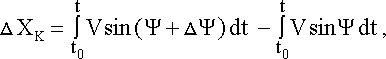
	(4.22)
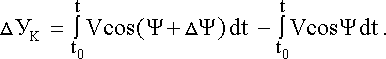
	(4.23)

V_г = V·cosq; V_хо = V·cosa·cosb; V_г  = V_хо·cosq/(cosa·cosb),   (4.24)

здесь Vг – горизонтальная составляющая истинной воздушной скорости; q – угол наклона траектории; a – угол атаки; b – угол скольжения.

Навигационный автомат получает от датчика скорости составляющую Vх истинной воздушной скорости вдоль оси приѐмника воздушных давлений, отличающуюся от фактической осевой составляющей скорости Vхо на величину DVх = Vх – Vхо. Предположим, что на летательном аппарате отсутствуют измерители углов атаки и скольжения, а в навигационном автомате не учитывается угол наклона траектории. Погрешности навигационного автомата, вызванные указанными выше причинами, будут:

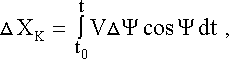
	(4.25)
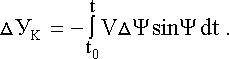
	(4.26)

Наиболее существенные погрешности счисления пути, вызванные углом скольжения , и погрешности датчика скорости DVх. Влияние углов атаки и наклона траектории сказываются в меньшей степени. Так, например, при постоянных углах a= b=q = 1° погрешности счисления пути от угла скольжения составляют 1,75%, а от углов атаки и наклона траектории – 0,03% от пройденного расстояния. Для маневренных летательных аппаратов углы q могут меняться в широких пределах, вследствие чего погрешности счисления пути могут оказаться значительными. Чтобы уменьшить эти погрешности, необходимо использовать сигналы гировертикали, датчиков углов атаки и скольжения для вычисления горизонтальной составляющей Vг истинной воздушной скорости.

Погрешности навигационных автоматов, вызванные погрешностями определения курса

Поскольку в вычислителе осуществляется интегрирование функций VsinY и VcosY, то для выяснения влияния погрешности датчика курса важно определить, является ли его погрешность независимой от времени, или функцией времени. С этой точки зрения погрешности датчика курса можно разделить на две группы: 1) независимые от времени погрешности (девиация, застой и др.); 2) периодические во времени погрешности (вызванные колебаниями в следящей системе или колебаниями чувствительного элемента); поворотные погрешности – не периодические, но зависимые от времени. Полагая скорость ветра U = 0 и обозначив независимые от времени погрешности датчика курса через DY, получим значения погрешностей навигационного автомата DХк, DУк:

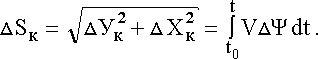
	(4.32)
	(4.33)

Полагая DY малым, имеем

sinDY = DY;  cosDY = 1;

sin(Y + DY) = sinY + DYcosY; cos(Y + DY) = cosY – DYsinY.

Тогда

	(4.34)
	(4.35)

Полная погрешность DSк равна

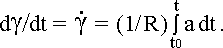
(4.36)

При V = const                          DS_к = V·t·DY = S·DY,                         (4.37)

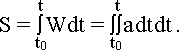
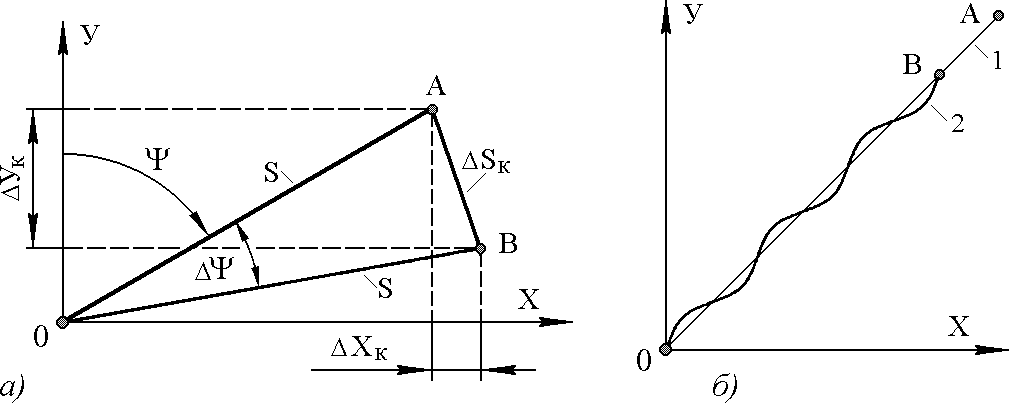
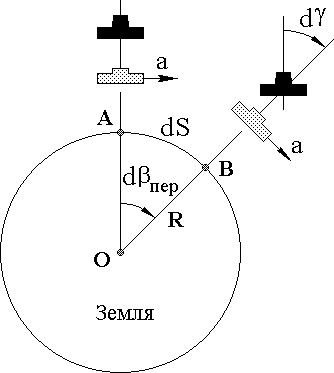
здесь S – путь, пройденный летательным аппаратом за время t по кратчайшему расстоянию от точки вылета. На рис. 4.4, а показано геометрическое построение, на основании которого может быть найдена погрешность DSк навигационного автомата при известной ошибке DY датчика курса; здесь OA = OB = S.

Рис. 4.4. Погрешности навигационного автомата, вызванные погрешностями датчика курса

Рассмотрим влияние периодических погрешностей датчика курса на показания навигационного автомата. Положим, что датчик курса выдаѐт навигационному автомату курс

Y = Y_ср + DY_~,                                     (4.38)

здесь Yср – средний курс, при отсутствии постоянной погрешности является истинным курсом;

DY~ – периодическая погрешность датчика курса.

Возникающая при этом погрешность навигационного автомата может быть получена из простейших геометрических построений. На рис. 4.4, б кривая 1 представляет истинную траекторию летательного аппарата, кривая 2 – кажущуюся (отсчитываемую навигационным автоматом) траекторию, которая имеет вид волнообразной линии вследствие периодических погрешностей датчика курса.

Длины кривых 1 и 2 одинаковы. Точка A определяет истинное местоположение ЛА, точка B – кажущееся местоположение, отсчитываемое навигационным автоматом.

Вследствие периодической погрешности датчика курса навигационный автомат будет всегда показывать расстояние меньше истинного.

 Периодические погрешности датчика курса с большой амплитудой недопустимы