Экваториальная система координат. Положение светила в этой системе определяется прямым восхождением и склонением (рис. 1.10).

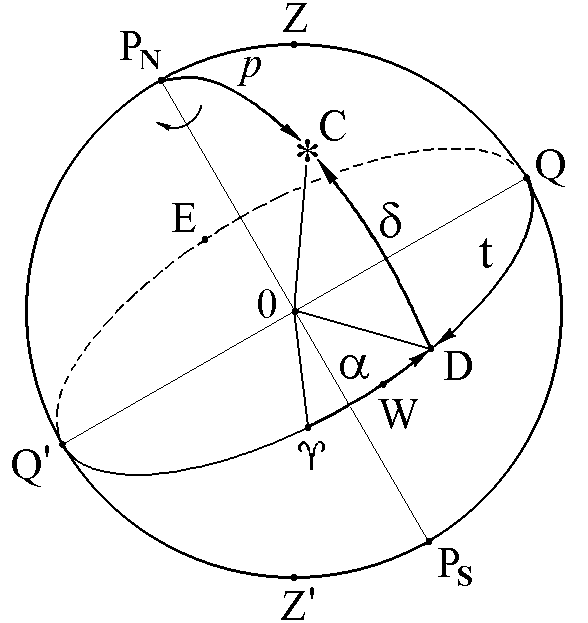
Рис. 1.10. Экваториальные координаты светила:

α – прямое восхождение;

δ – склонение; p – полярное расстояние; t – местный часовой угол; ОВЕН – точка весеннего равноденствия

Прямое восхождение α – двугранный угол между плоскостью круга склонения точки весеннего равноденствия «ОВЕН» и плоскостью круга склонения светила. Прямое восхождение измеряется дугой экватора ОВЕНD, отсчитывается от точки ОВЕН против движения часовой стрелки от 0 до 360.

Склонение светила – угол между плоскостью небесного экватора и направлением из центра небесной сферы на светило. Склонение может принимать значения от 0 до +90 в северной полусфере и от 0 до –90 в южной полусфере.

Иногда вместо склонения пользуются полярным расстоянием светила p, которое дополняет склонение светила до 90:  δ + p = 90. (1.8)

Для решения некоторых задач в этой системе небесных координат положение светила относительно небесного меридиана определяют местным часовым углом.

Местный часовой угол светила t – двугранный угол между плоскостью небесного меридиана и плоскостью круга склонения светила. Местный часовой угол t измеряется дугой экватора QD, отсчитывается от точки Q на запад от 0 до 360. Иногда местный часовой угол отсчитывают к востоку, в этом случае его обозначают t E и называют восточным. Восточный часовой угол дополняет западный часовой угол светила до 360:

t + t E = 360. (1.9)

Для наблюдателя, находящегося на гринвичском (нулевом) меридиане местный часовой угол светила называют гринвичским часовым углом светила t гр. Прямое восхождение и склонение светила вследствие видимого суточного вращения небесной сферы не изменяются, а часовой угол изменяется равномерно. Местный часовой угол светила отсчитывается от небесного меридиана, в плоскости которого располагается географический меридиан наблюдателя. В один и тот же момент времени разность

местных часовых углов светила равна разности долгот наблюдателей t 2 – t 1 = λ2 – λ1 , (1.10) полагая λ 1 = 0, t1 = t гр , t 2 = t, λ2 = λ, получим t = t гр + λ. (1.11)

Экваториальные координаты светил приводятся в авиационном астрономическом ежегоднике. Экваториальные координаты светил изменяются вследствие трѐх причин: собственного видимого движения по небесной сфере (например, Солнце, планеты, Луна), прецессии и нутации земной оси. Наибольшей скоростью видимого собственного движения по небесной сфере обладают Луна и Солнце. По причине изменения координат

звѐзд устаревают такие понятия, как Таблицы высот и азимутов звѐзд (ТВАЗ). Поэтому срок годности ТВАЗ равен 8 годам.

5. Время и его измерение. Звѐздное время, истинное солнечное и среднее солнечное время; местное, поясное, летнее время; линия перемены дат.

Измерение времени по движению небесных светил. Промежуток времени между двумя последовательными одноимёнными кульминациями точки весеннего равноденствия на одном и том же географическом меридиане называется звѐздными сутками. Местное звѐздное время S в данный момент численно равно часовому углу точки весеннего равноденствия (рис. 1.11). Точка весеннего равноденствия на небе ничем не отмечена. Рис. 1.11. Измерение звѐздного времени

Непосредственно измерить еѐ часовой угол нельзя. Поэтому для установления звѐздного времени надо измерить часовой угол t какого-либо светила, прямое восхождение α которого известно, тогда S = t_ОВЕН = α + t. (1.12)Если исходным меридианом при определении местного звѐздного времени является гринвичский меридиан, то это время называют гринвичским звѐздным временем и обозначают S гр . Значения S гр на каждый час гринвичского времени соответствующей даты даются в ААЕ. Звѐздное время не связано с Солнцем, поэтому пользоваться им в повседневной жизни неудобно. Промежуток времени между двумя последовательными одноимѐнными кульминациями центра солнечного диска на одном и том же географическом меридиане называют истинными солнечными сутками. Истинное солнечное время в данный момент численно равно местному часовому углу центра солнечного диска плюс 12 часов: T = t + 12 h . (1.13)

Вследствие неравномерного движения Солнца по эклиптике и наклона эклиптики к экватору истинные солнечные сутки не имеют одинаковой продолжительности в течение года. Среднее солнце – фиктивная точка, равномерно движущаяся по небесному экватору и совершающая полный оборот за год. Промежуток времени между двумя последовательными одноимѐнными кульминациями среднего солнца на одном и том же географическом меридиане называют средними солнечными сутками. Их Продолжительность равна среднему значению продолжительности истинных солнечных суток за год. За начало средних солнечных суток на данном географическом меридиане принимается момент нижней кульминации среднего солнца (средняя полночь). Время, протекшее от нижней кульминации среднего солнца до любого другого его положения, называется средним солнечным временем или просто средним временем. Среднее время в данный момент численно равно местному часовому углу среднего солнца плюс 12 часов: T m = t m + 12 h. Разность между средним временем и истинным солнечным временем в один и тот же момент называется уравнением времени (Е). Значение Е можно определить по графику рис. 1.12. Среднее солнечное время равно истинному солнечному времени плюс уравнение времени: T m = T + Е. (1.15) Таким образом, измерив непосредственно часовой угол Солнца t , определяют по (1.13) истинное солнечное время и, зная уравнение времени Е в этот момент, находят по (1.15) среднее солнечное время T m = t + 12 h + Е. Так как среднее солнце проходит через меридиан как раньше, так и позже истинного Солнца, разность их часовых углов (уравнение времени) может быть как положительной, так и отрицательной величиной. По среднему солнечному времени Tm определяют поясное Тп и летнее Тл время: T п = T m – λ + N, (1.16) Т л = Т п + 1, (1.17) здесь N – номер часового пояса.