Расчет поршня
Поршень воспринимает нагрузки от давления сжимаемого пара хладоагента, сил инерции и трения. Расчету на прочность подлежат: днище, бобышка, стенка.
Днище поршня рассчитывают на изгиб от действия сил давления пара. Днище рассматривают как круглую плиту с опорным сечением по окружности R СР.
Максимальное напряжение в поршне возникает в центре плиты. В этом случае точка приложения равнодействующей от равномерно распределённой нагрузки находимая в (цилиндре) центре тяжести днища.
Координата центра тяжести половины днища, х, м, рассчитывается по формуле
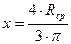, (1)
где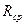 
- средний радиус опорного сечения, м.
Средний радиус опорного сечения, 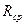, м, рассчитывается по формуле
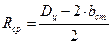. (2)
Реакция от поршневой силы будет приложена в центре тяжести дуги опорного сечения. При этом координата центра тяжести опорного сечения, у, м, определяется по формуле
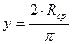. (3)
 |
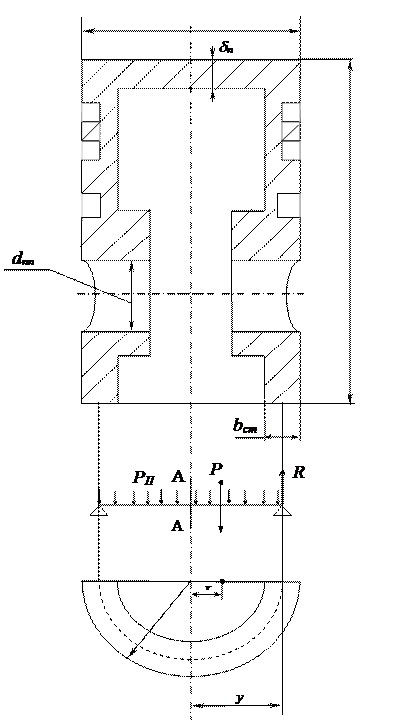Рисунок 1 – Расчетная схема поршня
Равнодействующая от поршневой силы Р, Н, определяется по формуле
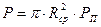. (4)
где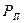 
- максимальная поршневая сила, действующая на поршень за цикл движения, Н.
Тогда реакция от поршневой силы R, Н, определяется по формуле
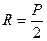. (5)
Изгибающий моменты в сечении А, Ми, Н×м, определяется по формуле
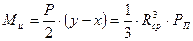. (6)
Напряжение изгиба в сечении А,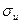 
, Па, определяется по формуле
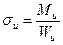, (7)
где W и – момент сопротивления в сечении, м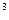 
.
Для прямоугольного сечения днища поршня момент сопротивления в сечении, W и , м 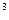, определяется по формуле
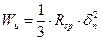. (8)
или
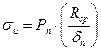. (9)
Допустимые напряжение принимаются в зависимости от материала из которого изготовлен поршень и составляют для:
- стали - [ s и ] = 100…120 МПа;
- алюминия - [ s и ] до 40 МПа.
Расчет гильзы цилиндра
Гильзу цилиндра рассматривают как тонкостенный сосуд испытываемый пробным гидравлическим давлением со стороны высокого давления. Стенку гильзы цилиндра рассчитывают на растяжение.
 |
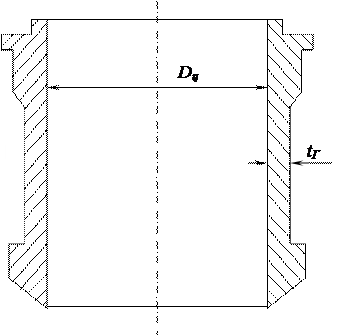Рисунок 2 – Расчетная схема гильзы цилиндра
Напряжение растяжения в стенке гильзы σр, МПа, определяется по формуле
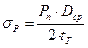, (10)
где Рп – растягивающее усилие, действующее на стенку гильзы, МПа;
D ср – средний диаметр гильзы цилиндра, м.
Растягивающее усилие, действующее на стенку гильзы Рп, МПа, определяется по формуле
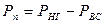. (11)
Допустимое напряжение растяжения для чугунных гильз составляет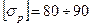 
МПа.
Расчет поршневого пальца
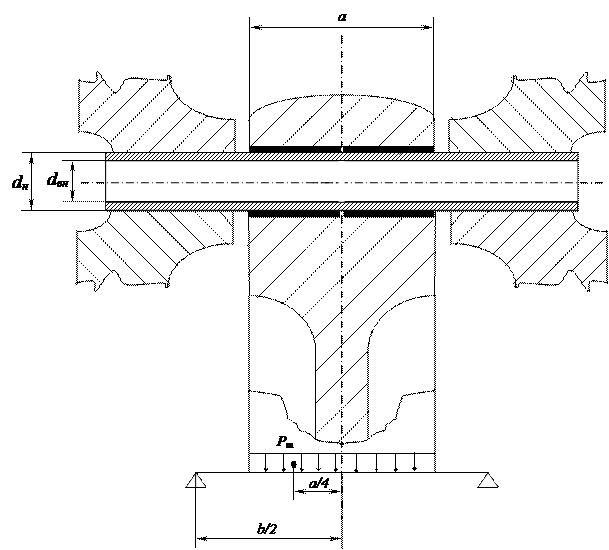
Рисунок 3 – Расчетная схема поршневого пальца
В общем случае максимальное напряжение изгиба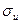 
, МПа, действующее в сечении поршневого пальца, определяется по формуле
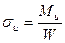, (12)
где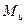 
- максимальный изгибающий момент для двух опорной балки, нагруженной равномерно-распределенной нагрузкой, Н·м;
W – момент сопротивления сечения поршневого пальца, м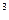 
.
Для рассматриваемой конструкции поршневого пальца напряжение изгиба 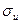, МПа, определяется по следующей формуле
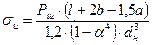, (13)
где Р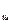 
- наибольшая по абсолютному значению сила, действующая на шатун, м;
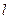- полная длина пальца, м;
b – расстояние между бобышками поршня, м;
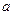- длина шатунного подшипника, м;
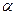- отношение внутреннего диаметра поршневого пальца к внешнему.
Поршневой палец также испытывается напряжения на срез q, МПа, определяемое следующей формулой
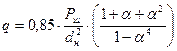. (14)
Расчет поршневого кольца
Кольца расположены в спиральных канавках в теле поршня.
При расчете поршневых колец на прочность определяют некоторые опасные напряжения изгиба, возникающие
- на внешних волокнах кольца в рабочем состоянии, s из1;
- на внутренних волокнах кольца при его надевании на поршень, s из2.
 |
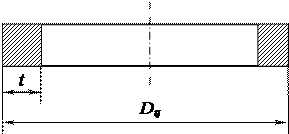Рисунок 4 – Расчетная схема поршневого кольца
Напряжение на внешних волокнах кольца,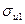 
, МПа, определяют по следующей формуле
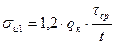, (15)
где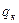 
- удельное давление кольца на стенки цилиндра, МПа;
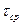- средний радиус кольца, м;
t – толщина кольца, м.
Удельное давление кольца на стенки цилиндра, 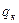, МПа, определяется по формуле
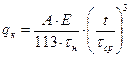, (16)
где Е– модуль упругости материала кольца, МПа;
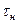- наружный радиус кольца, м;
А – величина замка по среднему диаметру кольца, м.
Для колец, выполненных из чугуна модуль упругости составляет:
Е = 8·10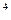 
МПа.
Величина замка по среднему диаметру кольца составляет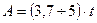 
, м.
Напряжение изгиба на внешних волокнах кольца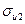 
, МПа, определяют по следующей формуле
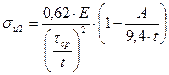. (17)
Допустимые напряжение для колец, выполненных из чугуна составляют:
, 
.
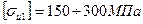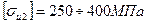Расчет шатуна
В течении одного оборота шатуна подвергается воздействию переменных сил растяжения, сжатия поэтому стержень шатуна рассчитывается на сжатие,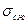 
, МПа в минимальном сечении
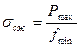, (18)
где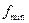 
- минимальное сечение (сечение А-А), м2;
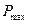- максимальная сила действующая на поршень, Н.
Стержень шатуна проверяется на устойчивость, при этом критическая опрокидывающая сила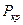 
, Н, определяется по формуле Тетмайера
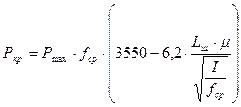, (19)
где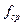 
- площадь шатуна в среднем сечении (сечение С-С), м 
;
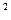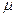- коэффициент заделки;
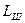- длина шатуна, м;
I – момент инерции сечения относительно соответствующей оси, м4.
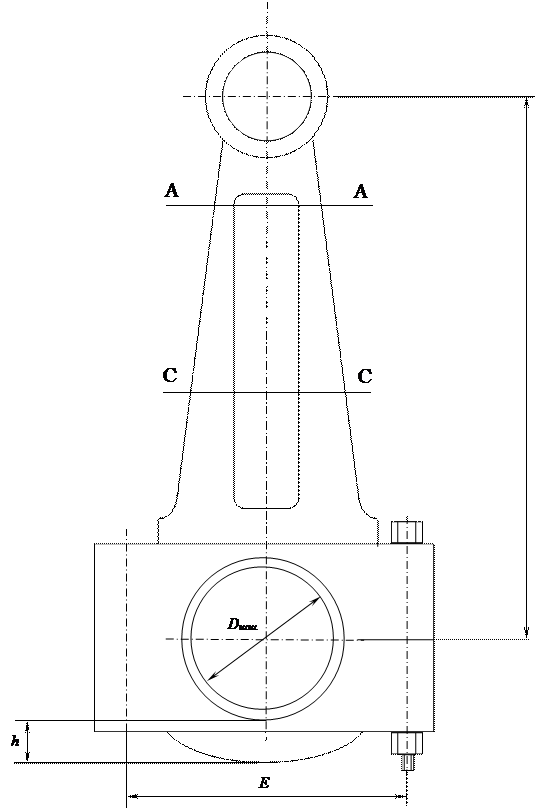
Рисунок 5 – Расчетная схема шатуна
Рисунок 6 – Расчетная схема сечения стержня шатуна
Момент инерции сечения относительно соответствующей оси, I , м4, определяется по следующим выражениям
- для оси хх: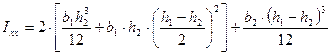 
, (20)
- для оси yy: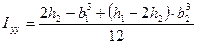 
. (21)
Запас устойчивости стержня шатуна n определяется по формуле
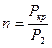, (22)
где Р2 – сила, действующая на шатун от давление нагнетания в цилиндре компрессора, Н.
Для обеспечения устойчивости шатуна запас должен составлять не менее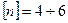 
.
Расчет нижней головки шатуна.
На нижнюю головку шатуна действует сила инерции I 0, Н, которая определяется по формуле
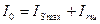, (23)
где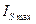 
- максимальная сила инерции возвратно поступательно движущихся частей, Н;
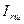- сила инерции вращающихся частей шатуна, Н.
Сила инерции вращающихся частей шатуна,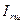 
, Н определяется по формуле
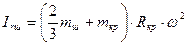, (24)
где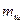 
- масса шатуна, кг;
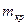- масса крышки шатуна, кг;
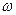- средняя окружная скорость маховика, м/с;
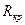- радиус кривошипа, м.
Максимальное напряжение в средней части крышки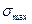 
, МПа, определяется по формуле
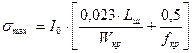, (25)
где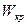 
- момент сопротивления сечения крышки шатуна, м 
;
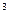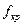- площадь сечения крышки шатуна, м .
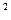Момент сопротивления сечения крышки шатуна 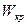, м 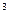, определяется по формуле
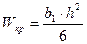. (26)
Допустимое напряжение для шатуна изготовленного из чугуна составляет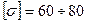 
МПа.
Расчет шатунного болта
Дата: 2018-11-18, просмотров: 1162.
