ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ЛАБОРАТОРНЫМ РАБОТАМ
ПО ТЕОРИИ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Омск 2007
УДК 621.3
ББК 31.2
П
Составители:
Попов А.П., д-р техн. наук, проф. кафедры ТиОЭ;
Куракина О.П., канд. техн. наук, доц. кафедры ТиОЭ
Методические указания включают в себя описание лабораторного стенда и рекомендации по выполнению лабораторных работ по теории линейных электрических цепей курса «Теоретические основы электротехники», выполняемых на кафедре «Теоретическая и общая электротехника» ОмГТУ.
Все лабораторные работы проводятся на универсальном измерительном стенде. Лабораторный стенд состоит из лабораторного модуля (рис.1) и генераторно-измерительного модуля (рис.2).
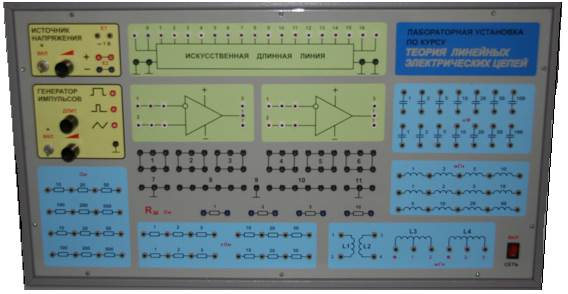
Рис.1
Лабораторный модуль
Включает в себя следующие составные части:
1. Магазин резисторов.
2. Магазин конденсаторов.
3. Магазин катушек индуктивности.
4. Коммутационное поле.
5. Искусственную длинную линию.
6. Два операционных усилителя.
7. Источник переменного напряжения Е1.
8. Источник постоянного напряжения Е2.
9. Генератор импульсов.
10. Плату питания.
1. Магазин резисторов состоит из постоянных резисторов сопротивлением от 1 Ом до 50 кОм, объединенных в три группы. Резисторы 1 Ом, 2 Ом, 5 Ом и 10 Ом предназначены для использования в качестве шунтов. Все резисторы подобраны с отклонением не более ± 3 % от указанного номинала.
2. Магазин конденсаторов состоит из постоянных конденсаторов емкостью от 1 нФ до 100 нФ, подобранных с отклонением не более ± 1,5 % от указанного номинала. Наличие в магазине двух одинаковых групп конденсаторов позволяет составлять цепи с симметричными (одинаковыми) звеньями.
3. Магазин катушек индуктивности состоит из четырех групп катушек. Две группы катушек - с постоянной индуктивностью от 1 мГн до 10 мГн, подобранных с отклонением не более ± 5 % от указанного номинала. Объединение катушек в две одинаковые группы облегчает набор индуктивности необходимой величины и позволяет составлять цепи с симметричными (одинаковыми) звеньями. Третья группа катушек с большой индуктивностью от 5 до 50 мГн может быть эффективно использована для изучения переходных процессов в цепях первого и второго порядка. Четвертая группа включает в себя индуктивно связанные катушки.
4. Коммутационное поле предназначено для соединения элементов магазинов резисторов, конденсаторов и катушек индуктивности в исследуемые электрические цепи и подключения контрольно-измерительной аппаратуры. Соединение производится с помощью проводников со штепселями на концах. Поле состоит из гнезд, объединенных в группы. Две группы гнезд соединены с корпусом установки.
5. 16-звенная искусственная длинная линия позволяет исследовать процессы в цепях с распределенными параметрами при гармоническом и импульсном воздействии.
6. Два операционных усилителя с гнездами для подключения внешних элементов позволяют собирать и исследовать схемы аналоговых сумматоров, дифференцирующих и интегрирующих усилителей, активных фильтров, фазовращателей и генераторов. Напряжение питания на усилители подается при включении установки.
Для обеспечения начальной устойчивости выход каждого усилителя соединен с инвертирующим входом через резистор 1 мОм, а неинвертирующий вход с общим проводом («корпусом») через резистор 1 мОм.
7. Источник переменного напряжения Е1 вырабатывает напряжение около 1 В частотой 50 Гц. Защищен от короткого замыкания.
8. Источник постоянного напряжения Е2 служит для исследования электрических цепей в режиме постоянного тока. Выходное напряжение регулируется в пределах (1,3 – 11) В. Источник защищен от перегрузок и короткого замыкания. Имеет звуковую сигнализацию перегрузки. Схема защиты срабатывает при токе (100 – 150) мА. Для возвращения источника в рабочее состояние после срабатывания схемы защиты необходимо устранить причину перегрузки, выключить источник напряжения тумблером «ВКЛ.» и снова включить.
9. Генератор импульсов предназначен для исследования переходных и импульсных характеристик цепей.
Генератор формирует:
– прямоугольные положительные импульсы U1 с длительностью Т/2, изменяемой резистором «ДЛИТ.», в пределах от 200 мкс до 1000 мкс. Амплитуда импульсов регулируется переменным резистором в пределах 0 - 1, 5 В. Выходное сопротивление генератора 5,0 Ом. Выход защищен от короткого замыкания в течение не более 30 секунд;
– прямоугольные положительные импульсы U2 с нерегулируемой длительностью 2-3 мкс. Амплитуда импульсов регулируется переменным резистором в пределах 0 - 1, 5 В. Выходное сопротивление генератора 5,0 Ом. Выход защищен от короткого замыкания без ограничения длительности;
– симметричное относительно 0 В пилообразное напряжение U3 с нерегулируемой амплитудой 1,5 В. Крутизна пилообразного напряжения изменяется переменным резистором «ДЛИТ.». Выходное сопротивление генератора 1000 Ом. Выход защищен от короткого замыкания без ограничения длительности.
На левой боковой панели установки расположены три гнезда для подключения к входу синхронизации осциллографа, что дает возможность студентам подробно рассмотреть передний фронт импульсов генератора и начало переходных процессов в изучаемых электрических цепях. Среднее гнездо – корпус установки. Импульсы синхронизации U4 и U5 на правом и левом гнездах имеют разную полярность, что позволяет использовать для работы с установкой различные типы осциллографов.
10. Плата питания вырабатывает постоянные напряжения ±15 В для работы генератора импульсов и операционных усилителей, +20 В для источника напряжения Е2, переменное напряжение 1 В для источника напряжения Е1.
Электропитание лабораторного модуля осуществляется от сети переменного напряжения 220 В. Для заземления установки служит клемма заземления, расположенная на тыльной стороне корпуса.

Рис. 2
Вольтметр
В генераторно-измерительный модуль встроены 3 вольтметра, позволяющие измерять как постоянные напряжения, так и действующие значения переменных напряжений частотой от 200 Гц до 125 кГц.
Вход вольтметра гальванически не связан с корпусом установки, поэтому в режиме измерения постоянных напряжений вольтметры могут быть подключены к любым точкам исследуемой цепи.
Однако, следует учесть, что гнездо «-» входа вольтметра связано с общей шиной схемы вольтметра и имеет значительную емкость относительно корпуса установки. Поэтому при измерении переменных напряжений частотой выше 5 кГц во избежание существенных ошибок показаний следует подключать гнездо «-» входа вольтметра к точкам исследуемой цепи, соединенным с гнездами «^» или находящимся под меньшим переменным напряжением относительно «^».
Вольтметр имеет 3 предела измерения: 200 мВ; 2 В; 20 В .
Относительная погрешность измерения постоянного напряжения – не более 2 % от измеряемой величины при условии
0,1. UПИ < UИЗМ < UПИ ,
где UПИ - предел измерения; UИЗМ - измеряемое напряжение.
Относительная погрешность измерения переменного гармонического напряжения частотой от 200 Гц до 125 кГц – не более 4 % от измеряемой величины при условии
0,1. UПИ < UИЗМ < UПИ
Абсолютная погрешность измерения за счет «ухода нуля» и погрешности дискретности – не более 6 единиц наименьшего разряда счета.
Входное сопротивление вольтметра – 1 МОм.
Входная емкость – не более 20 пФ.
Фазометр
Фазометр позволяет измерять фазовый сдвиг между двумя синусоидальными напряжениями, поданными на входы А и Б:
Dj= jБ - jА
Характеристики фазометра:
пределы измерения фазового сдвига -180 град. < j < +180 град.;
индикация - цифровая трехразрядная (отрицательные значения фазового сдвига индицируются горением светодиода левее знакового индикатора);
минимальное напряжение на входах фазометра, при котором обеспечивается его устойчивая работа – 80 мВ;
максимальное напряжение на входах фазометра, при котором обеспечивается его устойчивая работа – 2,5 В;
частотный диапазон устойчивой работы фазометра - 200 Гц – 100 кГц;
погрешность измерения фазового сдвига в диапазоне ½4 град.< j <176 град.½ при обеспечении устойчивой работы фазометра – не более 1 град.;
входное сопротивление фазометра - не менее 1 МОм;
входная емкость - не более 20 пФ;
Гнезда «^» не соединены с корпусом установки.
Во избежание неустойчивой работы фазометра и связанных с этим ошибок измерения рекомендуется контролировать величину входных напряжений фазометра с помощью вольтметров, подключаемых параллельно его входам.
При отсутствии входных напряжений или их несоответствии вышеуказанным значениям фазометр индицирует любое возможное значение фазового сдвига.
ОБЩИЕ ТРЕБОВАНИЯ
ПО ПОДГОТОВКЕ, ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ
ОТЧЕТОВ ПО ЛАБОРАТОРНЫМ РАБОТАМ
Лабораторные занятия являются составной частью учебного курса «Теоретические основы электротехники».
Они ставят своей целью:
– содействовать лучшему усвоению содержания курса ТОЭ;
– обучать методике и технике электротехнического лабораторного эксперимента;
– научить студентов правильному истолкованию результатов экспериментов на основе полученных теоретических знаний, как с количественной, так и с качественной стороны.
Подготовка к лабораторной работе
При подготовке к лабораторной работе студент, ознакомившись с соответствующим описанием, должен:
1) заготовить бланк отчёта по лабораторной работе с необходимыми таблицами и схемами;
2) выполнить домашнюю подготовку к работе и включить её в бланк отчёта;
3) четко представлять методику сборки схемы и эксперимента.
Выполнение лабораторной работы
До начала проведения экспериментальной части лабораторной работы каждый студент проходит собеседование с преподавателем. После собеседования студент получают разрешение преподавателя приступить к сборке электрической схемы. Проверка схемы производится преподавателем или лаборантом, после чего дается разрешение на подключение к схеме источника напряжения. После окончания экспериментальной части работы, студенты, не разбирая схемы, производят необходимые расчеты, заполняют соответствующие таблицы, строят необходимые кривые, векторные диаграммы и т.д. Убедившись в полном выполнении объема работы, а также в правильности полученных данных, преподаватель разрешает разобрать схему.
Оформление отчетов по лабораторным работам
Подробное содержание отчета приведено в руководстве к каждой работе. Отчет должен иметь титульный лист, на котором указывается наименование института и кафедры, номер и наименование работы, фамилия и инициалы студента, номер группы.
СПИСОК ЛИТЕРАТУРЫ
1. Бессонов Л. А. Теоретические основы электротехники. Электрические цепи: Учеб. – 11 изд. – М.: Гардарики, 2001. – 638 с.
2. Теоретические основы электротехники: в 3-х т. Учебник для вузов.
Том 1. – 4-е изд. / К. С. Демирчян, Л. Р. Нейман, Н. В. Коровкин, В. Л. Чечурин. – СПб.: Питер, 2003. – 463 с.
3. Основы теории цепей. / Г. В. Зевеке, П. А. Ионкин, А. В. Нетушил. – М.: Энергия, 1989. – 529 с.
4. Теоретические основы электротехники: Сб. задач с решениями. Пособие для студентов вузов по направлению “Электроэнергетика”, 3-е изд., перераб. и доп. – Омск: Изд-во ОмГТУ, 2005. – 253 с.
Лабораторная работа №1
Цель работы
Экспериментальное исследование соотношений для токов и напряжений электрических цепей синусоидального тока с катушкой индуктивности и ёмкостью.
Краткая теория
В однофазных электрических цепях в большинстве случаев действует ЭДС, изменяющаяся по синусоидальному закону.
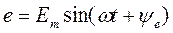 ,
,
где 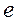 - мгновенное значение ЭДС,
- мгновенное значение ЭДС,
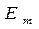 - амплитудное значение,
- амплитудное значение,
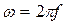 - угловая частота,
- угловая частота,
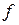 - частота,
- частота,
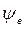 - начальная фаза,
- начальная фаза,
Токи и напряжения в таких цепях также синусоидальны:
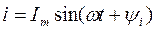 ;
;
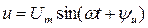 .
.
Фазовый сдвиг между напряжением и током:
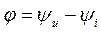 .
.
Наряду с мгновенным и амплитудным используется понятие о среднеквадратичном (действующем) значении переменного тока, а также напряжения, ЭДС.
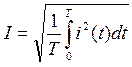 .
.
Физический смысл действующего значения синусоидального тока состоит в следующем: это такое значение постоянного тока, который за время, равное периоду синусоидального тока в некотором сопротивлении R выделяет такое же количество тепла что и синусоидальный ток.
Действующее значение синусоидального тока можно определить через его амплитудное значение:
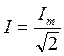 .
.
В большинстве случаев расчёт цепей синусоидального тока производят комплексным методом. Он позволяет осуществить переход от тригонометрических уравнений к алгебраическим, составленным относительно комплексов тока и напряжения.
Известно, что синусоидально изменяющаяся величина может быть условно (символически) представлена в виде комплексного числа 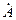 . Это лежит в основе замены синусоидальных функций вращающимися векторами на комплексной плоскости (рис. 1).
. Это лежит в основе замены синусоидальных функций вращающимися векторами на комплексной плоскости (рис. 1).

Рис. 1
Проекция вектора 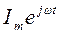 на мнимую ось для момента времени t:
на мнимую ось для момента времени t:
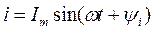 .
.
Совокупность векторов, изображающих синусоидально изменяющиеся токи, напряжения, ЭДС некоторой электрической цепи, называется векторной диаграммой. Векторные диаграммы строятся для момента времени t = 0.
Анализ цепей синусоидального тока необходимо проводить с учётом следующих пассивных элементов: резисторов, катушек индуктивности и конденсаторов, которые характеризуются соответственно активным сопротивлением R, индуктивностью L (индуктивным сопротивлением 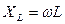 ) и ёмкостью C (ёмкостным сопротивлением
) и ёмкостью C (ёмкостным сопротивлением 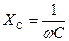 ). Комплексные сопротивления индуктивности и ёмкости соответственно можно найти как
). Комплексные сопротивления индуктивности и ёмкости соответственно можно найти как
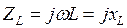 ;
; 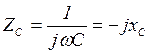 .
.
Реальная катушка индуктивности обладает существенным электрическим сопротивлением и может быть представлена эквивалентной схемой, состоящей из последовательно включенных индуктивности 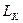 и активного сопротивления Rk (рис. 2). Векторная диаграмма для такой катушки приведена на рис. 3.
и активного сопротивления Rk (рис. 2). Векторная диаграмма для такой катушки приведена на рис. 3.

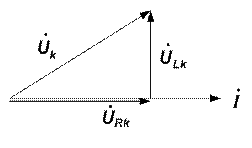
Рис. 2 Рис. 3
Ток в цепи (рис. 4, рис. 5), состоящей из последовательно соединённых элементов, находиться по закону Ома
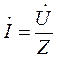 ,
,
где Z – входное комплексное сопротивление цепи, равное сумме сопротивлений отдельных её элементов:
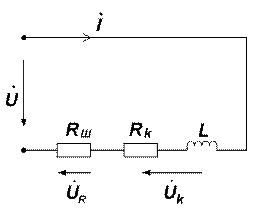
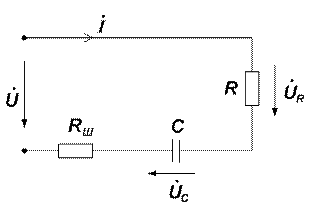
Рис. 4 Рис. 5
Для схемы рис. 4 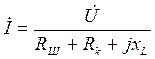 ;
;
для схемы рис. 5 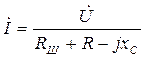 .
.
3. Задание для самостоятельной подготовки
3.1. По литературе [1] или [2] ознакомьтесь с теорией цепей однофазного синусоидального тока. Необходимо освоить расчёты в комплексной форме, перевод комплексных величин из алгебраической формы в показательную и обратно, построение векторных диаграмм токов и напряжений. Примеры расчета простейших схем приведены в [4].
3.2. Рассчитать величину индуктивности L, если индуктивное сопротивление 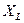 на частоте
на частоте 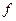 =50 Гц равно 10 Ом. Чему будет равно индуктивное сопротивление рассматриваемой индуктивности на частоте
=50 Гц равно 10 Ом. Чему будет равно индуктивное сопротивление рассматриваемой индуктивности на частоте 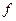 =100 кГц?
=100 кГц?
3.3. На частоте 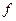 =100 кГц для последовательного соединения индуктивности предыдущего п.3.2 и резистора R = 35 Ом рассчитать комплексное сопротивление. Запишите результат в алгебраической и показательной формах.
=100 кГц для последовательного соединения индуктивности предыдущего п.3.2 и резистора R = 35 Ом рассчитать комплексное сопротивление. Запишите результат в алгебраической и показательной формах.
3.4. Рассчитать мгновенное значение тока в этой цепи (п.3.3), если к ней приложено напряжение 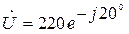 В. Постройте векторную диаграмму.
В. Постройте векторную диаграмму.
3.5. Рассчитать величину ёмкости, если ёмкостное сопротивление 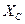 на частоте
на частоте 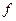 =20 кГц равно 25 Ом. Чему будет равно сопротивление этой ёмкости на частоте 400 кГц?
=20 кГц равно 25 Ом. Чему будет равно сопротивление этой ёмкости на частоте 400 кГц?
3.6. Для последовательного соединения ёмкости предыдущего п.3.5 и резистора R = 150 Ом рассчитать комплексное сопротивление, полное сопротивление и аргумент комплексного сопротивления, его активную и реактивную составляющие на частоте 10 кГц.
3.7. Рассчитать (схема рис. 4) величины токов и напряжений, указанных в табл. 1 и записать их мгновенные значения. Величина действующего входного напряжения задаётся преподавателем U = (0,4 - 1) В, 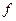 = 300 Гц;
= 300 Гц;
L = 10 мГн; Rk = 11 Ом; R = 10 Ом.
Таблица 1
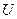 , В , В
| 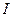 , А , А
| 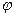 , град , град
| 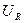 , В , В
| 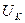 , В , В
| 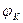 , град , град
| 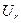 , В , В
| 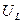 , В , В
| |
| Расчет | ||||||||
| Опыт |
3.8. Рассчитать для схемы рис. 5 величины токов и напряжений, указанных в табл. 2 и записать их мгновенное значение, если U = (0,4 - 1) В, 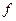 = 4 кГц; C = 25 нФ; R = 1 кОм;
= 4 кГц; C = 25 нФ; R = 1 кОм; 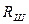 = 10 Ом.
= 10 Ом.
Таблица 2
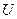 , В , В
| 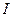 , А , А
| 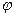 , град , град
| 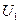 , В , В
| 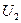 ,В ,В
| |
| Расчет | |||||
| Опыт |
3.9. Перечертить экспериментальные схемы рассматриваемой работы (рис. 6-9).
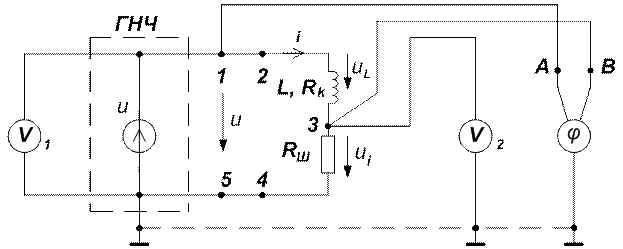
Рис. 6
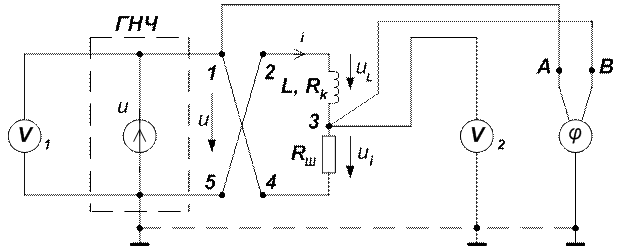
Рис. 7
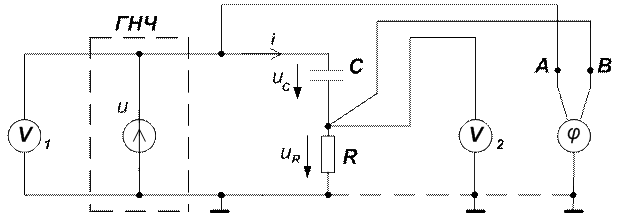
Рис. 8
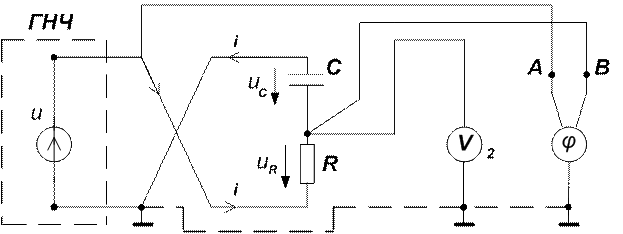
Рис. 9
Цель работы
Целью работы является исследование цепи с магнитно-связанными катушками.
Краткая теория
В состав электрических цепей могут входить катушки, магнитно-связанные между собой. Поток одной пронизывает витки других и наводит в них ЭДС взаимоиндукции, которые необходимо учесть в расчете. Наличие индуктивных связей между ветвями 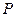 и
и 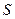 электрической цепи при составлении уравнений по второму закону Кирхгофа учитывается путем введения дополнительных напряжений от взаимной индукции в соответствующие ветви:
электрической цепи при составлении уравнений по второму закону Кирхгофа учитывается путем введения дополнительных напряжений от взаимной индукции в соответствующие ветви:
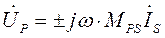 ;
; 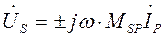 ,
,
где 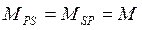 - взаимная индуктивность между ветвями P и S.
- взаимная индуктивность между ветвями P и S.
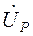 - действующее значение комплексного напряжения взаимной индукции, возникающего в P - ой ветви от тока, протекающего в S ветви;
- действующее значение комплексного напряжения взаимной индукции, возникающего в P - ой ветви от тока, протекающего в S ветви;
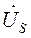 - действующее значение комплексного напряжения взаимной индукции, возникающего в S ветви от тока, протекающего в P – ой ветви.
- действующее значение комплексного напряжения взаимной индукции, возникающего в S ветви от тока, протекающего в P – ой ветви.
Знак «плюс» у напряжения взаимной индукции соответствует согласному направлению потоков само- и взаимоиндукции катушек, знак «минус» - встречному.
При анализе цепи необходимо знать, как включены катушки, - согласно или встречно. Если на схеме токи магнитно-связанных катушек одинаково ориентированы относительно одноименно обозначенных зажимов катушек (например, точками или звездочками), то это согласное включение, в противном случае - встречное.
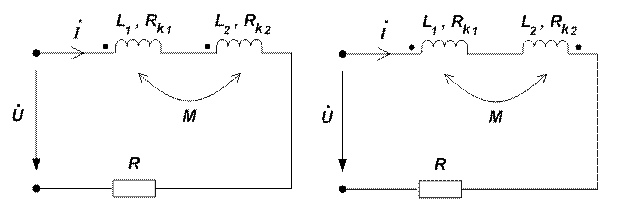
Рис. 1 Рис. 2
На схеме (рис. 1) катушки включены согласно. В этом случае по второму закону Кирхгоффа в комплексной форме можно записать
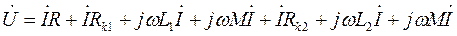 ,
,
где Rk1 и Rk2 - активные сопротивления проводников, которыми намотаны катушки L 1 и L 2 .
Обозначим входное комплексное сопротивление для согласного включения как
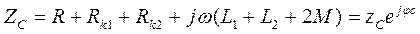 ,
,
где
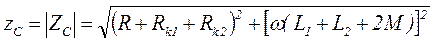 ;
;
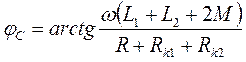 .
.
Тогда, принимая начальную фазу напряжения 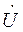 , ψu = 0 , получим
, ψu = 0 , получим
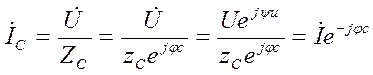 .
.
В случае встречного включения катушек (схема рис. 2)
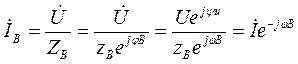 ,
,
где 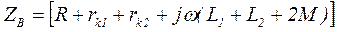 - входное комплексное сопротивление для встречного включения;
- входное комплексное сопротивление для встречного включения;
 ;
;
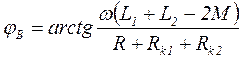 .
.
Обозначим: L ЭС =( L 1 + L 2 +2 M ) - эквивалентная индуктивность всей цепи при согласном включении катушек, L ЭВ =( L 1 + L 2–2 M ) - при встречном. Из двух опытов с согласным и встречным соединениями можно определить взаимную индуктивность
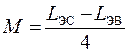 .
.
Существует еще один способ опытного определения взаимной индуктивности М. Подключим первую катушку к генератору синусоидальной ЭДС, а к зажимам второй катушки подключим вольтметр (рис. 3).
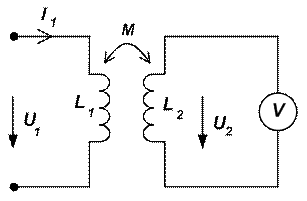
Рис. 3
Действующее значение напряжения U 2 , наводимого на вторичной катушке при синусоидальном токе, протекающем в первичной катушке, определяется выражением 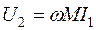 . Следовательно
. Следовательно 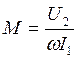 , т.е. измеряя ток I 1 и напряжение U 2 в режиме холостого хода (вольтметр обладает большим сопротивлением и I 2 ≈ 0 ).
, т.е. измеряя ток I 1 и напряжение U 2 в режиме холостого хода (вольтметр обладает большим сопротивлением и I 2 ≈ 0 ).
Степень индуктивной связи двух катушек характеризуется коэффициентом связи K св . В курсе ТОЭ показано, что 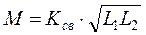 , т.е.
, т.е.
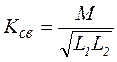 .
.
K св находится в пределах 0 ≤ K св ≤ 1 и зависит от расстояния между катушками; чем дальше они друг от друга, тем меньше значение K св . Если катушки размещаются на ферромагнитном сердечнике, то K св стремится к единице.
3. Задание для самостоятельной подготовки
3.1. По разделу 2 описания этой лабораторной работы и по одному из учебников [1], [2] ознакомьтесь с явлением взаимоиндукции, взаимной индуктивностью, ЭДС взаимоиндукции, согласным и встречным соединением магнитосвязанных катушек, а также способах определения взаимной индуктивности.
3.2. Рассчитать токи и напряжения в схемах рис. 1, 2, 3. Величина частоты 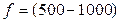 Гц и действующего значения входного напряжения
Гц и действующего значения входного напряжения 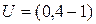 В задаётся преподавателем. Параметры элементов:
В задаётся преподавателем. Параметры элементов: 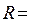 1 Ом;
1 Ом;
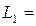 8,4 мГн;
8,4 мГн; 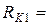 14,6 Ом;
14,6 Ом; 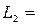 5,1 мГн;
5,1 мГн; 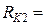 1 Ом;
1 Ом; 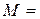 4,4 мГн.
4,4 мГн.
Результаты расчётов записать в табл. 1.
3.3. По результатам расчётов п.3.2 построить в масштабе векторную диаграмму.
Таблица 1
| Включение катушек | U, В | I, А | φ, град | LЭ, Гн | ZВХ, Ом | M, Гн | Kсв | M, Гн из опыта 4.2 | |
| согласное | расчет | ||||||||
| опыт | |||||||||
| встречное | расчет | ||||||||
| опыт | |||||||||
Лабораторная работа № 3
Резонанс напряжений
Цель работы
Исследование явления резонанса напряжений в R , L , C цепи.
Краткая теория
Для режима резонанса в цепи, представленной на рис. 1, характерна возможность возникновения равных по модулю и противоположных по фазе напряжений на индуктивности катушки и конденсаторе, существенно превышающих напряжение питания цепи U (отсюда название – резонанс напряжений).
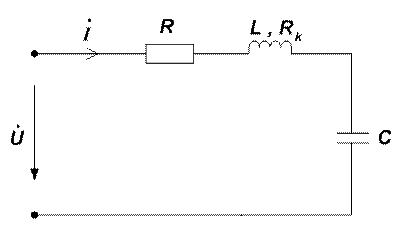
Рис. 1
Условие резонанса напряжений в последовательном контуре – равенство индуктивного сопротивления катушки XL и емкостного сопротивления конденсатора XC .
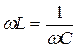 .
.
Из этого соотношения видно, что резонанса в цепи можно достичь, варьируя либо частотой приложенного напряжения, либо параметрами 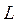 и
и 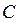 , либо тем и другим одновременно.
, либо тем и другим одновременно.
В частности, если 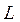 и
и 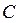 фиксированы, то для резонансной частоты получаем
фиксированы, то для резонансной частоты получаем
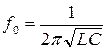 .
.
Резонансный контур характеризуется следующими параметрами:
– волновым сопротивлением 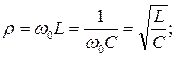
– добротностью контура 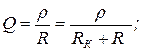
– параметром затухания 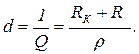
В данной работе исследование явления резонанса осуществляется изменением частоты 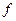 источника напряжения, и при этом рассчитываются
источника напряжения, и при этом рассчитываются
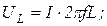
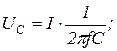
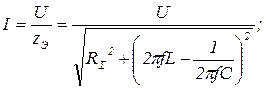
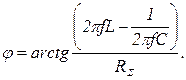
Так как при резонансе полное сопротивление минимально 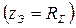 , то при постоянстве действующего значения напряжения цепи ток максимален:
, то при постоянстве действующего значения напряжения цепи ток максимален:
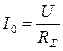 ,
,
где RΣ = R + RK .
Падение напряжения на индуктивности катушки и на емкости конденсатора при резонансе в силу равенства 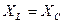 равны друг другу и сдвинуты по фазе почти на 1800 относительно друг друга, если RK << R. Частотные характеристики
равны друг другу и сдвинуты по фазе почти на 1800 относительно друг друга, если RK << R. Частотные характеристики 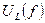 и
и 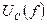 также как и
также как и 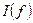 , как показано выше, имеют максимум, причем максимум
, как показано выше, имеют максимум, причем максимум 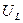 наступает при частоте
наступает при частоте
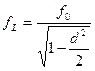 ,
,
а максимум 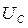 при частоте
при частоте
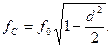
Из этих выражений видно, что с уменьшением величины RΣ или коэффициента затухания 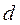 , величины
, величины 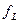 и
и 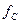 стремятся к
стремятся к 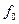 и максимумы напряжений
и максимумы напряжений  и
и 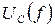 совмещаются. При возрастании RΣ, наоборот, максимумы расходятся.
совмещаются. При возрастании RΣ, наоборот, максимумы расходятся.
3. Задание для самостоятельной подготовки
3.1. По литературе [1] следует ознакомиться с разделом курса ТОЭ по резонансу напряжений.
3.2. Перечертить схему исследования (рис. 2.). Здесь емкость С = 100 нФ, сопротивление катушки R К = 27,6 Ом, индуктивность катушки 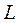 = 50 мГн, сопротивление R Ш = 10 Ом.
= 50 мГн, сопротивление R Ш = 10 Ом.
Величина напряжения источника питания ГНЧ задается преподавателем 0 < U ≤ 1 В.
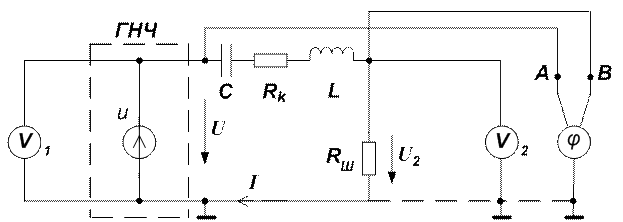
Рис 2
3.3. Используя исходные данные п.3.2 рассчитать следующие величины:
– резонансную частоту 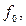 Гц;
Гц;
– волновое сопротивление 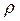 , Ом;
, Ом;
– добротность контура 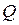 ;
;
– параметр затухания 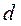 ;
;
– ток в контуре при резонансе 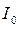 при заданном напряжении, А
при заданном напряжении, А
– напряжение на реактивной катушке и конденсаторе при резонансе, В
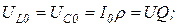
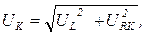 где
где 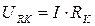 .
.
3.4. Рассчитать и построить графики зависимости 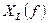 ;
; 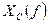 ;
; 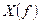 и
и 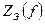 при изменении частоты от резонансной
при изменении частоты от резонансной 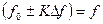 через интервалы
через интервалы 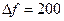 Гц в пределах
Гц в пределах
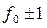 кГц (где
кГц (где 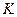 =0, 1, 2, 3, 4, 5).
=0, 1, 2, 3, 4, 5).
3.5. Рассчитать и построить графики зависимостей 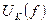 ;
; 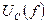 ;
; 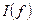 и
и 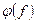 при тех же значениях частоты.
при тех же значениях частоты.
3.6. Расчетные данные п.п. 4 и 5 занести в табл. 1.
Таблица 1
| Час тота, Гц. | Опыт | Расчет | ||||||||||
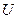 ,
В ,
В
| 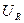 ,
В ,
В
| 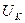 ,
В ,
В
| 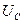 ,
В ,
В
| 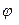 ,
град ,
град
| 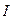 ,
А ,
А
| 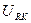 ,
В ,
В
| 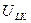 ,
В ,
В
| 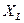 ,
Ом ,
Ом
| 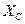 ,
Ом ,
Ом
| 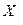 ,
Ом ,
Ом
| 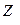 ,
Ом ,
Ом
| |
Цель работы
Целью работы является практическое знакомство и исследование явления резонанса в цепи, состоящей из параллельно включенных катушки индуктивности и емкости.
Краткая теория
В режиме резонанса в цепи, предоставляющей параллельное соединение катушки индуктивности и конденсатора, в катушке и конденсаторе возникают токи, многократно превышающие ток на входе цепи (отсюда и название - резонанс токов).
Рассматриваемая электрическая цепь, показанная на рис.1, представляет собой параллельный колебательный контур с потерями энергии, обусловленными резисторами. Для упрощения проведения испытаний резонанса в параллельном контуре в цепь введены одинаковые по модулю величины резисторы R .
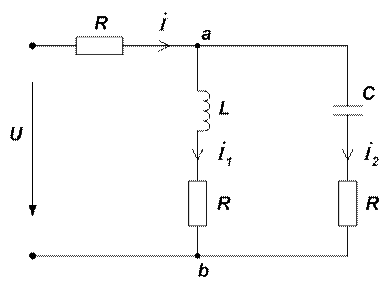
Рис. 1
Эквивалентная проводимость параллельного контура между точками «а» и «б» определяется выражением
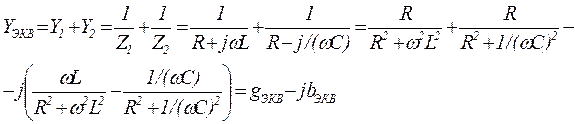 (1)
(1)
Условие резонанса определяется равенством нулю мнимой части входной проводимости параллельного контура 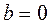 , т.е из (1) получаем (заменяя ω на ωР)
, т.е из (1) получаем (заменяя ω на ωР)
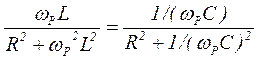 (2)
(2)
В этом случае входное сопротивление будет чисто активным, а в идеальном случае, когда R → 0, стремится к бесконечности.
Из (2) получаем значение резонансной частоты параллельного контура при условии, если R во всех ветвях одинаковы по величине.
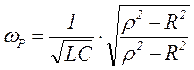 , (3)
, (3)
где 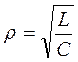 - волновое (характеристическое) сопротивление. В идеальном контуре, когда R → 0, как видно из (3)
- волновое (характеристическое) сопротивление. В идеальном контуре, когда R → 0, как видно из (3) 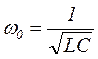 , т.е. такое же значение частоты как и в последовательном контуре.
, т.е. такое же значение частоты как и в последовательном контуре.
Определим теперь эквивалентное сопротивление параллельного контура относительно точек а, б (см. рис. 1) на резонансной частоте используя (1), учитывая что реактивная проводимость b при резонансе равно нулю.
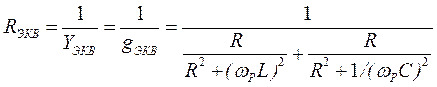 (4)
(4)
Подставляя в (4) значение ωР , вычисленное по формуле (3), получаем возможность рассчитать эквивалентное сопротивление рассматриваемого контура. (Если активные сопротивления, включенные в ветвях, не равны между собой, то получается более сложное выражение для RЭКВ и ωР ).
Из (4) видно, что в идеальном контуре, когда R = 0, то RЭКВ → ∞.
Ток в неразветвленной части при резонансе можно определить следующим образом (учитывая, что сам контур обладает чисто активным сопротивлением):
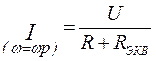 , где I, U – действующие значения. (5)
, где I, U – действующие значения. (5)
Токи в параллельных ветвях также легко определяются на основании (5) по закону Ома
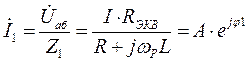
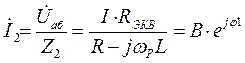
Сдвиг по фазе между токами 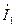 и
и 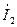 Δφ = φ1 - φ2 = 1800 (при малых значениях R, т.е. когда ωРL >> R и 1/ωРС >> R ).
Δφ = φ1 - φ2 = 1800 (при малых значениях R, т.е. когда ωРL >> R и 1/ωРС >> R ).
Как видно из рис. 1, ток 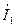 при резонансе должен отставать от напряжения
при резонансе должен отставать от напряжения 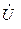 по фазе почти на 900, а ток
по фазе почти на 900, а ток 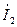 - опережать напряжение
- опережать напряжение 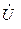 почти на 900 при малых значениях R.
почти на 900 при малых значениях R.
3. Задание для самостоятельной подготовки
3.1. По учебнику [1] следует дополнительно ознакомиться с основами теории параллельного колебательного контура.
3.2. Рассчитать электрическую цепь (рис. 1) при напряжении 0 < U ≤ 1 (задается преподавателем), С = 100 нФ, L = 50 мГн, R = 10 Ом. Расчету подлежат следующие параметры:
- резонансная частота идеального контура f0=ω0/2π, Гц;
- резонансная частота исследуемого контура fР, Гц;
- волновое сопротивление исследуемого контура 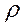 , Ом;
, Ом;
- эквивалентное сопротивление исследуемого контура при резонансе (ω = ωР) RЭКВ , Ом;
- ток в неразветвленной части цепи на частоте резонанса (ω = ωР) I, А;
3.3. Рассчитать и построить график зависимости ZЭКВ = 1/YЭКВ при изменении частоты от резонансной 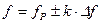 , где
, где 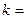 0, 1, 2, 3, 4, 5,
0, 1, 2, 3, 4, 5, 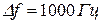 , в пределах
, в пределах 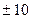
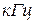 .
.
3.4. Рассчитать токи 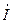 ,
, 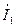 ,
, 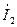 и построить на комплексной плоскости векторную диаграмму для токов
и построить на комплексной плоскости векторную диаграмму для токов 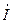 ,
, 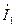 ,
, 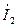 ,
, 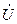 .
.
3.5. По графику зависимости ZЭКВ от частоты определить добротность контура (Q = fР/Δf)
Расчетные данные п. 3.4 занести в табл. 1.
Таблица 1
| Частота, Гц | Опыт | Расчет | ||||
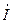 , А , А
| 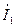 , А , А
| 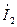 , А , А
| I, А | I1, А | I2, А | |
| fР – 1000 | ||||||
| fР - 800 | ||||||
| fР - 600 | ||||||
| fР - 400 | ||||||
| fР - 200 | ||||||
| fР | ||||||
| fР + 200 | ||||||
| fР + 400 | ||||||
| fР + 600 | ||||||
| fР + 800 | ||||||
| fР + 1000 | ||||||
4. Методические указания по проведению работы
4.1. Работа выполняется на лабораторном модуле универсально измерительного лабораторного стенда. С помощью перемычек собирается электрическая цепь (рис. 2), которая подключается к генератору синусоидально изменяющегося напряжения во времени в диапазоне частот от 200 Гц до 10 кГц.
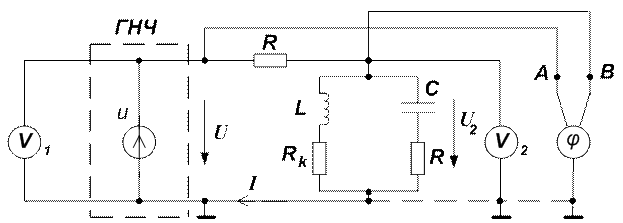
Рис. 2
Значения токов в ветвях определяются с помощью цифрового вольтметра путем измерения падения напряжения на образцовых резисторах 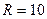 Ом, с последующим вычислением тока по закону Ома, т.е.
Ом, с последующим вычислением тока по закону Ома, т.е. 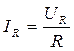 . Измерения сдвига фаз
. Измерения сдвига фаз 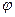 между напряжением на контуре
между напряжением на контуре 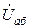 и токами
и токами 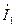 и
и 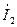 осуществляется с помощью электронного фазометра (вначале провод А фазометра подключается к ветви с катушкой индуктивности, затем к ветви с конденсатором. В первом случае измеряется сдвиг по фазе между напряжением
осуществляется с помощью электронного фазометра (вначале провод А фазометра подключается к ветви с катушкой индуктивности, затем к ветви с конденсатором. В первом случае измеряется сдвиг по фазе между напряжением 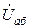 и током
и током 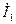 , во втором – между этим же напряжением
, во втором – между этим же напряжением 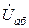 и током
и током 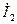 ).
).
4.2. Включить ГНЧ. Установить входное напряжение U (задается преподавателем).
4.3. Изменяя частоту генератора в окрестности расчетного значения резонансной частоты 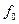 , найти опытное значение резонансной частоты по нулевому показанию фазометра или по минимуму тока I в неразветвленной части цепи.
, найти опытное значение резонансной частоты по нулевому показанию фазометра или по минимуму тока I в неразветвленной части цепи.
4.4. При изменении частоты от резонансной 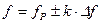 , где
, где 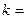 0, 1, 2, 3, 4, 5,
0, 1, 2, 3, 4, 5, 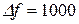 Гц, в пределах
Гц, в пределах 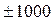 Гц снять частотные характеристики
Гц снять частотные характеристики 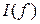 ,
, 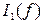 ,
, 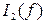 .
.
4.5. На резонансной частоте определить сдвиг по фазе между напряжением 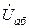 и токами
и токами 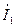 ,
, 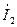 .
.
4.6. Экспериментальные данные п.п. 3. занести в табл. 1. Построить графики зависимостей (опытные и расчетные) 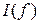 ,
, 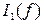 ,
, 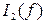 и сравнить их.
и сравнить их.
4.7. Построить векторную диаграмму для токов 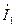 ,
, 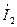 и напряжения
и напряжения 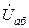 на комплексной плоскости. Начальную фазу напряжения
на комплексной плоскости. Начальную фазу напряжения 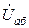 принять равной нулю.
принять равной нулю.
5. Контрольные вопросы
5.1. Запишите условие резонанса токов для идеального и реального параллельного контура.
5.2. Приведите формулы, по которым можно рассчитать активную, реактивную и полную проводимости параллельного контура на любой частоте, рис. 1.
5.3. Каким образом можно экспериментально изменить резонансную частоту?
5.4. Какими способами можно определить добротность параллельного RLC - контура?
5.5. Почему входное сопротивление идеального контура бесконечно большое?
5.6. Построить векторную диаграмму токов и напряжений для идеального и реального контуров.
Лабораторная работа №5
Переходные процессы в линейных электрических цепях с последовательным соединением R , L и R , C .
Цель работы
Исследование переходных процессов в простейших линейных электрических цепях при включении их под действие источников постоянного напряжения, а также переходных процессов возникающих при замыкании этих цепей.
2. Краткая теория
Переходный процесс, протекающий при включении R , L - цепи к источнику постоянной ЭДС Е (рис. 1) (ключ K мгновенно переключается из положения 2 в положение 1), описывается линейным, неоднородным дифференциальным уравнением первого порядка, составленным по второму закону Кирхгофа
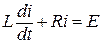 , (1)
, (1)
где 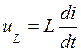 - напряжение самоиндукции, возникающее на катушке индуктивности L при изменении тока в ней.
- напряжение самоиндукции, возникающее на катушке индуктивности L при изменении тока в ней.
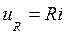 - напряжение на активном сопротивление R.
- напряжение на активном сопротивление R.
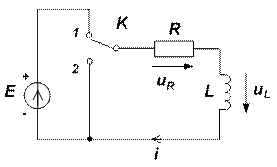

Рис. 1 Рис. 2
Решением этого дифференциального уравнения является следующая искомая функция, описывающая характер изменения тока во времени
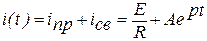 , (1)
, (1)
где 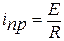 - принужденная составляющая тока (установившееся значение тока после коммутации);
- принужденная составляющая тока (установившееся значение тока после коммутации);
A – постоянная интегрирования;
p – корень характеристического уравнения.
Характеристическое уравнение
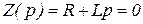 , откуда
, откуда 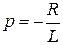 .
.
Полагаем, что до коммутации ток в цепи отсутствовал, т.е. при t = 0
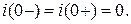
(2)
Из (1) следует, что 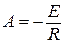 , а решения для тока и напряжения на индуктивности принимают вид:
, а решения для тока и напряжения на индуктивности принимают вид:
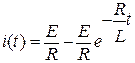 ;
; 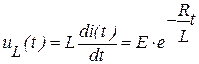 . (3)
. (3)
Как видно из выражения для 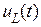 в момент срабатывания ключа (t = 0) на катушке скачком возникает ЭДС, по величине равная напряжению E. Затем uL ( t ) постепенно уменьшается до нуля из-за уменьшения скорости нарастания тока.
в момент срабатывания ключа (t = 0) на катушке скачком возникает ЭДС, по величине равная напряжению E. Затем uL ( t ) постепенно уменьшается до нуля из-за уменьшения скорости нарастания тока.
Графики изменения тока и напряжения на индуктивности приведены на рис. 2.
Рассмотрим теперь, что происходит в этой цепи в дальнейшем.
При отключении катушки с током от источника E (ключ K мгновенно переключается из положения 1 в положение 2), электрическая цепь принимает вид рис. 3.
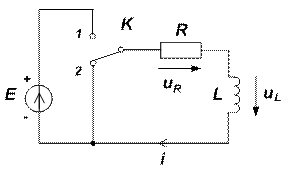
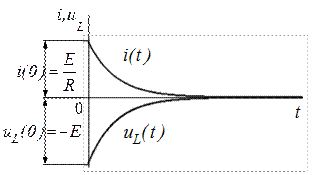
Рис. 3 Рис. 4
Переходный процесс описывается однородным дифференциальным уравнением, причем ток в момент коммутации (см. 3) на основании первого закона коммутации (ток в катушке не может измениться скачком) i (0)= 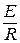 ,
,
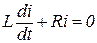 , решение которого имеет вид
, решение которого имеет вид
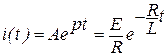 , (4)
, (4)
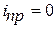 ,
, 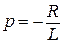 .
.
Напряжение на индуктивности
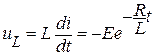 . (5)
. (5)
Как видно из (4) и (5) ток плавно уменьшается до нуля, а напряжение uL ( t ) скачком изменяет знак с (+) на (-). Это происходит потому, что ток в катушке не может измениться скачком и после отключения источника продолжает протекать в том же направлении, постепенно уменьшаясь по величине. При этом на катушке возникает напряжение обратной полярности, т.к. производная по току изменила свой знак. Графики изменения 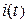 и
и 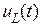 приведены на рис. 4.
приведены на рис. 4.
Скорость протекания переходного процесса характеризуется постоянной времени цепи 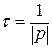 .
.
Постоянная времени численно равна времени за которое исследуемая функция изменяется в е раз. При экспериментальном исследовании переходных процессов постоянная времени цепи определяется графическим путем. Так как свободная составляющая тока или напряжения описывается
уравнением 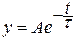 , производная в любой точки этой кривой
, производная в любой точки этой кривой
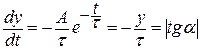 , следовательно, для определения постоянной
, следовательно, для определения постоянной
времени в этом случае можно измерить длину подкасательной, соответствующей какому либо значению у (рис 5) и умножить её на масштаб времени.
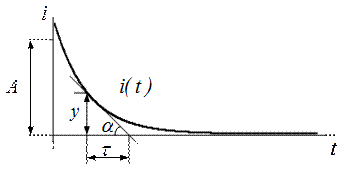
Рис. 5
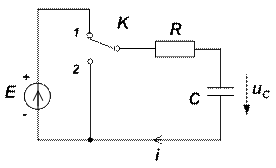
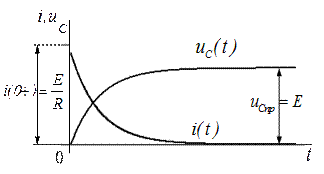
Рис. 6 Рис. 7
Рассмотрим процесс заряда конденсатора, т.е. каким образом будет нарастать с течением времени напряжение uC ( t ) (рис. 6) (ключ K мгновенно переключается из положения 2 в положение 1).
Общее решение для напряжения на емкости при решении задачи классическим методом имеет вид
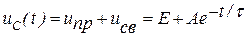 . (6)
. (6)
Полагаем, что до коммутации конденсатор не заряжен, т.е. при 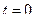 напряжение
напряжение 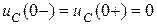 , а при
, а при 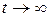 конденсатор должен зарядиться до напряжения, равного E, после чего ток станет равным нулю. Из (6) следует, что
конденсатор должен зарядиться до напряжения, равного E, после чего ток станет равным нулю. Из (6) следует, что 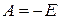 , а решения для тока и напряжения принимают вид
, а решения для тока и напряжения принимают вид
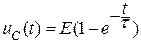 и
и 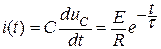 . (7)
. (7)
Графики изменения напряжения и тока в RC - цепи приведены на рис. 7. Они показывают, что напряжение на емкости не устанавливается мгновенно, а плавно изменяется по экспоненциальному закону от нуля до установившейся величины, равной Е; а ток в момент коммутации возрастает скачком до величины 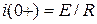 и затем плавно по экспоненциальному закону уменьшается до нуля.
и затем плавно по экспоненциальному закону уменьшается до нуля.
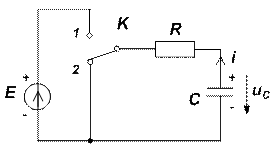
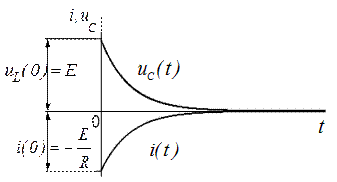
Рис. 8 Рис. 9
Если теперь мгновенно отключить источник E и мгновенно подключить к конденсатору сопротивление R, то начнется процесс разряда конденсатора. К этому моменту времени конденсатор зарядился до напряжения источника E, т.е. началом нового отсчета времени считаем uC (0+) = E. Тогда дифференциальное уравнение имеет вид
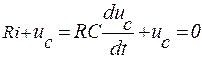 (8)
(8)
Принужденная составляющая uCпр = 0 и решение уравнения 8 имеет вид uC ( t ) = Aept. Так как uC (0-) = uC (0+) = E, 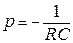 ,
, 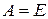 , то
, то
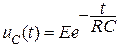 ,
, 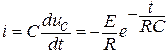 (9)
(9)
Графики изменения uC ( t ) и i ( t ) приведены на рисунке 9.
Цель работы
Экспериментальные и теоретические исследования переходных процессов в линейных электрических цепях второго порядка с двумя реактивными элементами.
Краткая теория
Рассмотрим переходный процесс в электрической цепи при периодическом подключении её с помощью ключа K (см. рис. 1) к источнику ЭДС. Это позволяет вырабатывать прямоугольные импульсы напряжения, действующие на R , L , C-цепь. Воздействие импульса длительностью, превышающей время переходного процесса электрической цепи, можно рассматривать как воздействие на цепь постоянной ЭДС Е. После окончания действия импульса, во время паузы, напряжение отсутствует, и этот режим работы цепи будет соответствовать мгновенному переключению ключа K из положения 1 в положение 2. При этом заряженный конденсатор будет разряжаться. Таким образом, переходные процессы в рассматриваемой R, L, C-цепи при воздействии прямоугольных импульсов следует рассматривать в двух режимах:
- включение электрической цепи под действие постоянного напряжения (рис. 1);
- разряд заряженного до напряжения E конденсатора через цепь R, L (рис. 5).
За счет применения электронного ключа и периодического переключения его из положения 1 в положение 2 и наоборот, появляется возможность наблюдать на экране осциллографа неподвижные осциллограммы для этих режимов.
Цель работы
Целью работы является определение параметров длинной линии, эквивалентной цепной схеме, состоящей из четырехполюсников; определение частоты источника напряжения, при которой цепная схема эквивалента заданному отрезку линии, а также исследование распределения действующего значения напряжения вдоль линии в режимах холостого хода и короткого замыкания.
Краткие сведения из теории
Длинную линию с распределёнными параметрами можно представить как схему с бесконечно большим числом элементарных звеньев, обладающих конечными значениями параметров. Такая замена будет давать тем более точные результаты, чем большее число звеньев будет содержать цепная схема.
На рис.1 показана цепная схема, представляющая собой соединение n – го числа симметричных Т – образных четырехполюсников.
При рассмотрении задачи будем полагать, что элементы схемы Т – образных четырехполюсников известны:
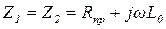 ;
; 
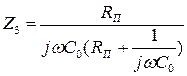 ,
,
где Rпр – продольное активное сопротивление единицы длины линии 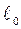 (например,
(например, 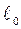 = 1 км);
= 1 км);
Rп – поперечное активное сопротивление утечки в линии длиной 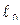 ;
;
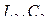 – индуктивность и емкость линии длиной
– индуктивность и емкость линии длиной 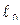 .
.
Определим параметры длинной линии, имеющей длину 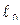 , которая эквивалентна одному звену, представляющему симметричный четырехполюсник, из которой построена цепная схема. Решение этой задачи известно и приведено в [1]. Рассмотрим ее решение в нужном нам толковании. Для Т – образной симметрической схемы четырехполюсника основные уравнения его имеют вид:
, которая эквивалентна одному звену, представляющему симметричный четырехполюсник, из которой построена цепная схема. Решение этой задачи известно и приведено в [1]. Рассмотрим ее решение в нужном нам толковании. Для Т – образной симметрической схемы четырехполюсника основные уравнения его имеют вид:

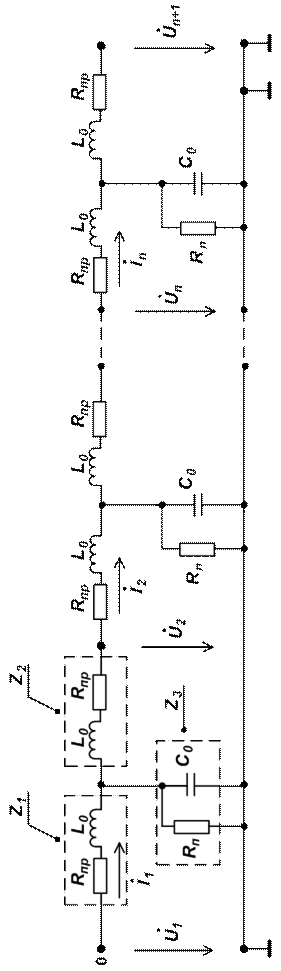
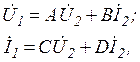 (1)
(1)
где 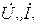 - напряжение и ток на входе;
- напряжение и ток на входе;
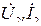 - напряжение и ток на выходе;
- напряжение и ток на выходе;
A, B, C, D – коэффициенты четырехполюсника, причем A = D .
Для длинной линии длины 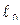 связь между
связь между 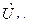
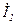 и
и 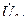
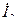 (напряжения и токи в конце и в начале линии) определяется уравнениями
(напряжения и токи в конце и в начале линии) определяется уравнениями
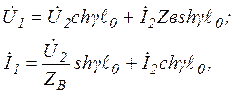 (2)
(2)
где Z В - волновое сопротивление, 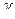 - постоянная распространения
- постоянная распространения 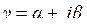 ,
, 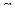 - коэффициент затухания падающей волны на единицу длины линии,
- коэффициент затухания падающей волны на единицу длины линии, 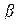 - коэффициент фазы, характеризует изменение фазы на единицу длины линии.
- коэффициент фазы, характеризует изменение фазы на единицу длины линии.
Учитывая, что элементы электрической схемы каждого четырехполюсника известны, то:
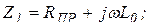
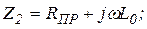
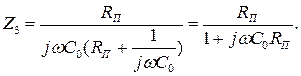
Параметры A , B , C , D, входящих в цепную схему четырехполюсников, выразим через известные значения Z 1 , Z 2 , Z 3 следующим образом [1, стр. 141]:
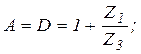
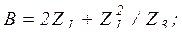
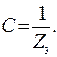 (3)
(3)
В рассматриваемой задаче по известным значениям A , B , C , D необходимо определить параметры эквивалентной линии. Этими искомыми параметрами, как уже ранее отмечалось, являются 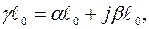
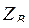 .
.
Если 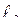 принять за единицу длины линии, то искомыми параметрами эквивалентной линии являются:
принять за единицу длины линии, то искомыми параметрами эквивалентной линии являются: 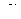 ,
,  ,
, 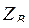 .
.
Определим теперь 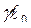 . Для этого используем соотношения (3) и аналогичные по форме записи уравнения (1) и (2).
. Для этого используем соотношения (3) и аналогичные по форме записи уравнения (1) и (2).
Из этой аналогии следует:
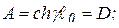
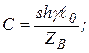
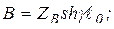
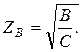 (4)
(4)
Для определения 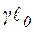 составим выражения для
составим выражения для 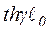 на основании (3) и (4),
на основании (3) и (4),
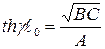 . (5)
. (5)
Как показано в [1], функцию 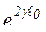 можно выразить следующим образом:
можно выразить следующим образом:
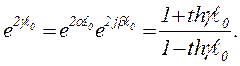 (6)
(6)
Подставляя в (6) значение 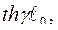 вычисленное по формуле (5) по известным A , B , C и представляя после вычисления числитель и знаменатель правой части (6) в показательной форме, находим значения
вычисленное по формуле (5) по известным A , B , C и представляя после вычисления числитель и знаменатель правой части (6) в показательной форме, находим значения 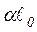 ,
, 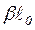 , т. е. определяем параметры линии, эквивалентной одному звену Т – образного симметричного четырехполюсника. При этом
, т. е. определяем параметры линии, эквивалентной одному звену Т – образного симметричного четырехполюсника. При этом 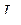 и
и 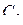 представляют собой соответственно индуктивность и емкость линии длиной
представляют собой соответственно индуктивность и емкость линии длиной 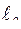 и имеют соответственно размерность Гн/м и Ф/м.
и имеют соответственно размерность Гн/м и Ф/м.
Если число звеньев цепной схемы равно n, то длина отрезка эквивалентной длинной линии будет в n – раз больше, т. е. равна 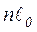 . Обозначим напряжение и ток на выходе n – го звена через
. Обозначим напряжение и ток на выходе n – го звена через 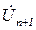 ,
, 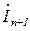 . Тогда напряжение и ток на входе первого звена:
. Тогда напряжение и ток на входе первого звена:
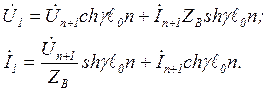
 (7)
(7)
На основании (7) напряжение и ток на входе k – го звена (k £ n)
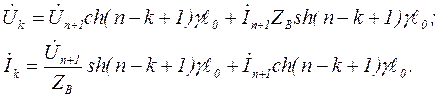 (8)
(8)
Как видно из (8), для того чтобы определить значение напряжения на входе или выходе любого звена (т. е. рассчитать распределение напряжения или тока вдоль цепной схемы) необходимо знать 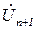 и
и 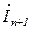 . Для этого предварительно необходимо провести опыт на определенной частоте по измерению напряжения и тока в конце линии
. Для этого предварительно необходимо провести опыт на определенной частоте по измерению напряжения и тока в конце линии 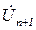 и
и 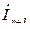 , либо задать их значения. После чего, используя (8), можно провести расчет в заданной цепной схеме распределение тока и напряжения в разных точках цепной схемы.
, либо задать их значения. После чего, используя (8), можно провести расчет в заданной цепной схеме распределение тока и напряжения в разных точках цепной схемы.
Рассмотрим теперь расчет частоты источника синусоидального напряжения на входе линии, при котором цепная схема будет эквивалентна заданному отрезку линии, равному, например, длине четвертьволнового отрезка линии, или полуволновому или любому другому отрезку линии, в который укладывается необходимое число полуволн.
Ответ на этот вопрос легко получить, если рассмотреть холостой ход линии 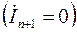 . При малых потерях аргументы гиперболических косинусов и синусов становятся чисто мнимыми
. При малых потерях аргументы гиперболических косинусов и синусов становятся чисто мнимыми 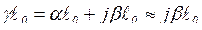 .
.
Тогда 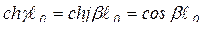 ;
; 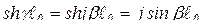 . (9)
. (9)
Для холостого хода 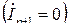 с учетом (9), получаем
с учетом (9), получаем
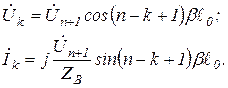 (10)
(10)
Пусть нас интересует частота питающего напряжения, на которой цепная схема моделирует четвертьволновой отрезок в режиме холостого хода. Ток на входе в этом случае должен иметь максимальное значение, а напряжение стремиться к нулю. Это возможно когда 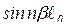 = 1, т. е. на основании (10) можем записать
= 1, т. е. на основании (10) можем записать
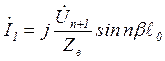 ;
; 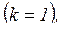
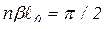 ;
;
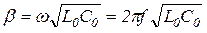 .
.
Следовательно: 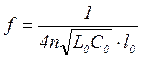 . (11)
. (11)
Если удвоить частоту источника синусоидального напряжения, то цепная схема будет эквивалентна полуволновому отрезку линии. При четырехкратном увеличении частоты данная цепная схема будет являться моделью линии, на длине которой указывается полная волна, и т. д.
Ниже на рис. 2 рис. 3 приведены результаты расчёта распределения напряжения и тока вдоль четвертьволнового отрезка линии в различных режимах его работы. При расчете распределения действующих значений напряжения и тока в режиме х.х. по формуле (8) принято U n+1 = 10 В, а при расчете распределения действующего значения напряжения и тока в режиме к.з. принято I n+1 = 1 A. При этом число звеньев принято n = 16 со следующими единичными параметрами длинной линии:
Lo = 390 мкГн/км; Co = 4,7 пФ/км; Rп = 150 кОм/км при различных значениях Rп, равных 1 Ом, 5 Ом, 10 Ом.
Частота питающего напряжения при этом определена по формуле (11) и соответствует f = 11541 Гц.




Рис. 2


Рис. 3
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОТЕХНИКИ
Дата: 2018-11-18, просмотров: 1161.