Методические указания
1. Число размещений из п элементов по т вычисляется по формуле 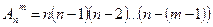 и соответствует числу соединений из п элементов по т, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком их расположения.
и соответствует числу соединений из п элементов по т, которые отличаются друг от друга либо самими элементами (хотя бы одним), либо порядком их расположения.
2. Перестановками из п элементов называют такие соединения из всех п элементов, которые отличаются друг от друга порядком расположения элементов. Число перестановок вычисляется по формуле 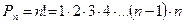 .
.
3. Сочетаниями из п элементов по т в каждом называются такие соединения, которые отличаются друг от друга хотя бы одним элементом. Число сочетаний находится по формуле 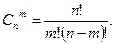
4. Вероятность события А вычисляется по формуле 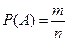 , где т – число исходов, благоприятствующих наступлению события А, п – общее число всех равновозможных несовместных исходов.
, где т – число исходов, благоприятствующих наступлению события А, п – общее число всех равновозможных несовместных исходов.
5. Математическое ожидание случайной величины (М(Х)) вычисляется по формуле 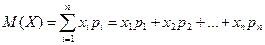 , где х i – значения случайной величины, р i – вероятности этих значений. Математическое ожидание называют средним значением случайной величины.
, где х i – значения случайной величины, р i – вероятности этих значений. Математическое ожидание называют средним значением случайной величины.
6. Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: Д(Х)=М[X-M(X)]2, или 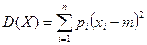 , где т=М(Х).
, где т=М(Х).
Пример 1. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5 при условии, что ни одна цифра в числе не повторяется?
Решение. Число перестановок из пяти элементов согласно формуле 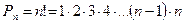 составляет
составляет 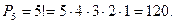 Значит различных пятизначных чисел можно составить 120.
Значит различных пятизначных чисел можно составить 120.
Пример 2. Сколько двузначных чисел можно составить из пяти цифр 1, 2, 3, 4, 5 при условии, что ни одна из них не повторится?
Решение. Так как двузначные числа отличаются друг от друга или самими цифрами или их порядком, то искомое количество равно числу размещений из 5 элементов по два элемента. Согласно формуле 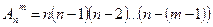
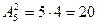 . Итак можно составить 20 различных двузначных чисел.
. Итак можно составить 20 различных двузначных чисел.
Пример3. Сколькими способами можно выбрать двух человек в президиум, если на собрании присутствует 64 человека?
Решение. Число пар выбранных в президиум отличаются друг от друга хотя бы одним человеком и равно числу сочетаний из 64 элементов по 2 элемента. Согласно формуле 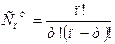
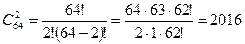 . Итак двух человек в президиум можно выбрать 2016 способами.
. Итак двух человек в президиум можно выбрать 2016 способами.
Пример 4. Из урны, в которой находятся 5 белых и 3 черных шара, вынимают 2 шара. Найти вероятность того, что оба шара окажутся черными.
Решение. Обозначим событие, состоящее в появлении двух черных шаров через А. Общее число возможных случаев п равно числу сочетаний из 8 элементов (5+3) по два: 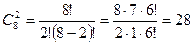 . Число случаев т, благоприятствующих событию А, равно числу сочетаний из 3 элементов по два элемента и составляет
. Число случаев т, благоприятствующих событию А, равно числу сочетаний из 3 элементов по два элемента и составляет 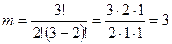 . По формуле
. По формуле 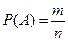 находим вероятность появления двух черных шаров:
находим вероятность появления двух черных шаров: 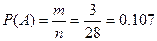 или 10,7%.
или 10,7%.
Пример 5. Найти математическое ожидание и дисперсию дискретной случайной величины, закон распределения которой задан таблицей
| Х | 3 | 4 | 5 | 6 | 7 |
| Р | 0,1 | 0,2 | 0,4 | 0,2 | 0,1 |
Решение. 1) В соответствии с формулой 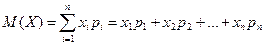 находим
находим
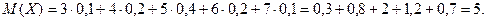
2) В соответствии с формулой 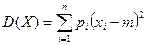 находим
находим
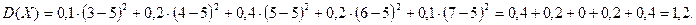
5. Контрольная работа (задания)
Вариант 1
1. Вычислите пределы функций:
1) 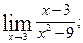 2)
2) 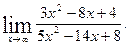
2. Найдите производную функции и вычислите:
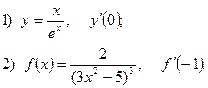
3. Найдите частные производные функции: 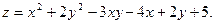
4. Найдите неопределенные интегралы:
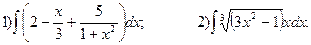
5. Вычислите определенные интегралы:
1) 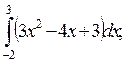 2)
2) 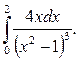
6. Найдите общее решение дифференциального уравнения:
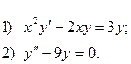
7. Вычислите по формуле прямоугольников 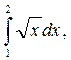 с точностью до 0,001, разбив интервал интегрирования на 10 частей.
с точностью до 0,001, разбив интервал интегрирования на 10 частей.
8. Решить систему уравнений по формулам Крамера:
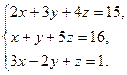
9. Найти: а) 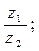 б)
б) 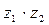 , в)
, в) 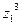 , если
, если 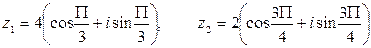 .
.
10. В урне 9 белых и 6 черных шаров. Из урны вынимают два шара. Какова вероятность того, что оба шара окажутся белыми?
Вариант 2
1.Вычислите пределы функций:
1) 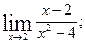 1)
1) 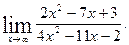
2. Найдите производную функции и вычислите:
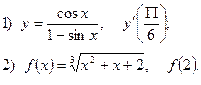
3.Найдите частные производные функции: 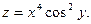
4.Найдите неопределенные интегралы:
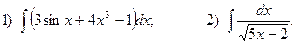
5. Вычислите определенные интегралы:
1) 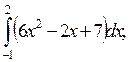 2)
2) 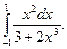
6. Найти общее решение дифференциального уравнения:
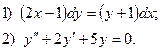
7. Вычислите по формуле трапеций 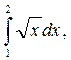 с точностью до 0,0001, разбив интервал интегрирования на 10 частей.
с точностью до 0,0001, разбив интервал интегрирования на 10 частей.
8. Решить систему уравнений методом Гаусса:
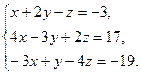
9. Найти: а) 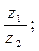 б)
б) 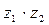 , в)
, в) 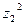 , если
, если 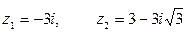 .
.
10. Найдите вероятность того, что при бросании двух игральных костей хотя бы один раз выпадет 6 очков.
Вариант 3
1.Вычислите пределы функций:
1) 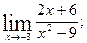 2)
2) 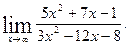
2. Найдите производную функции и вычислите:
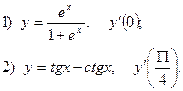
3. Найдите частные производные функции: 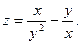
5. Найдите неопределенные интегралы:
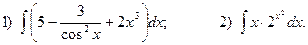
5. Вычислите определенные интегралы:
1) 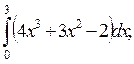 2)
2) 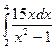
6. Найдите общее решение дифференциального уравнения:
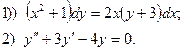
7. Вычислите по формуле трапеций 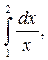 с точностью до 0,01, разбив интервал интегрирования на 5 частей.
с точностью до 0,01, разбив интервал интегрирования на 5 частей.
8. Решить систему уравнений по формулам Крамера:
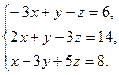
9. Найти: а) 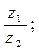 б)
б) 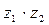 , в)
, в) 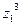 , если
, если 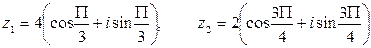 .
.
10. На стеллаже библиотеки в случайном порядке расставлено 15 учебников, причем 5 из них в переплете. Берут наудачу 3 учебника. Найдите вероятность того, что хотя бы 1 из взятых учебников окажется в переплете.
Вариант 4
1. Вычислите пределы функций:
а) 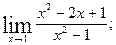 б)
б) 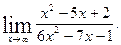
2. Найдите производную функции и вычислите:
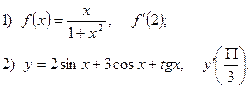
3.Найдите частные производные функции:
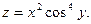
4.Найдите неопределенные интегралы:
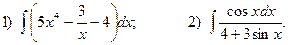
5. Вычислите определенные интегралы:
1) 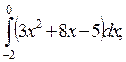 2)
2) 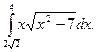
6. Найдите общее решение дифференциального уравнения:
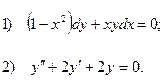
7. Вычислите по формуле трапеций 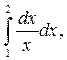 с точностью до 0,0001, разбив интервал интегрирования на 10 частей.
с точностью до 0,0001, разбив интервал интегрирования на 10 частей.
8. Решить систему уравнений методом Гаусса:
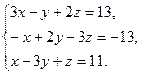
9. Найти: а) 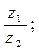 б)
б) 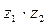 , в)
, в) 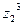 , если
, если 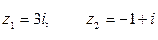 .
.
10. Даны вероятности значений случайной величины Х: значение 10 имеет вероятность 0,3; значение 2 – вероятность 0,4; значение 8 – вероятность 0,1; значение 4 – вероятность 0,2. Постройте ряд распределения случайной величины Х.
Вариант 5
1.Вычислите пределы функций:
1) 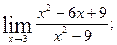 2)
2) 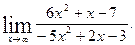
2. Найдите производную функции и вычислите:
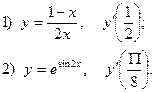
3.Найдите частные производные функции:
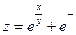
4.Найдите неопределенные интегралы:
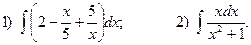
5. Вычислите определенные интегралы:
1) 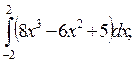 2)
2) 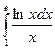
6. Найдите общее решение дифференциального уравнения:
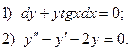
7. Вычислите по формуле прямоугольников 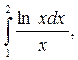 с точностью до 0,01, разбив интервал интегрирования на 4 части.
с точностью до 0,01, разбив интервал интегрирования на 4 части.
8. Решить систему уравнений по формулам Крамера:
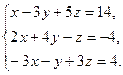
9. Найти: а) 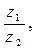 б)
б) 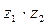 , в)
, в) 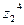 , если
, если 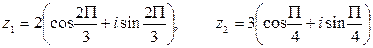 .
.
10. В партии из 8 деталей имеется 6 стандартных. Найдите вероятность того, что среди 5 взятых наугад деталей 3 стандартных.
Вариант 6
1.Вычислите пределы функций:
1) 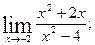 2)
2) 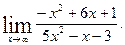
2. Найдите производную функции и вычислите:
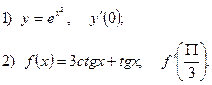
3.Найдите частные производные функции:
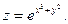
4.Найдите неопределенные интегралы:
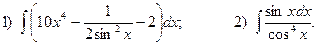
5. Вычислите определенные интегралы:
1) 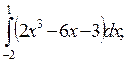 2)
2) 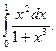
6. Найдите общее решение дифференциального уравнения:
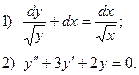
7. Вычислите по формуле трапеций 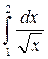 с точностью до 0,001, разбив интервал интегрирования на 10 частей.
с точностью до 0,001, разбив интервал интегрирования на 10 частей.
8. Решить систему уравнений методом Гаусса:
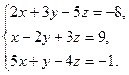
9. Найти: а) 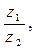 б)
б) 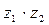 , в)
, в) 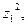 если
если 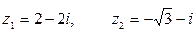 .
.
10. Случайная величина Х характеризуется рядом распределения:
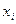
| 0 | 1 | 2 | 3 | 4 |
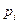
| 0,2 | 0,4 | 0,3 | 0,08 | 0,02 |
Определите математическое ожидание.
Вариант 7
1.Вычислите пределы функций:
1) 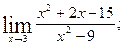 2)
2) 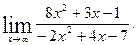
2. Найдите производную функции и вычислите:
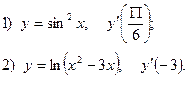
3.Найдите частные производные функции:
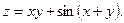
4.Найдите неопределенные интегралы:
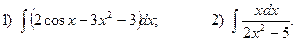
5. Вычислите определенные интегралы:
1) 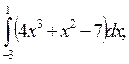 2)
2) 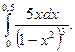
6. Найдите общее решение дифференциального уравнения:
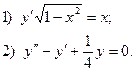
7. Вычислите по формуле прямоугольников 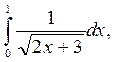 с точностью до 0,001, разбив интервал интегрирования на 8 частей.
с точностью до 0,001, разбив интервал интегрирования на 8 частей.
8. Решить систему уравнений по формулам Крамера:
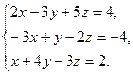
9. Найти а) 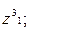 б)
б) 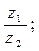 в)
в) 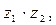 если
если 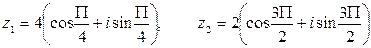 .
.
10. Имеется 100 лотерейных билетов. Известно, что на 5 билетов попадает выигрыш по 20 рублей, на 10 – по 15 рублей, на 15 – по 2 рубля и на остальные – ничего. Найдите вероятность того, что на купленный билет будет получен выигрыш не меньше 10 рублей.
Вариант 8
1.Вычислите пределы функций:
а) 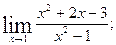 б)
б) 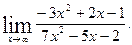
2. Найдите производную функции и вычислите:
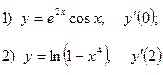
3.Найдите частные производные функции:
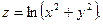
4.Найдите неопределенные интегралы:
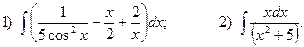
5. Вычислите определенные интегралы:
1) 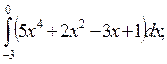 2)
2) 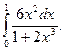
6. Найдите общее решение дифференциального уравнения:
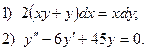
7. Вычислите по формуле трапеций 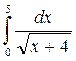 с точностью до 0,0001, разбив интервал интегрирования на 5 частей.
с точностью до 0,0001, разбив интервал интегрирования на 5 частей.
8. Решить систему уравнений методом Гаусса:
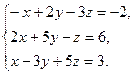
9. Найти а) 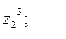 б)
б) 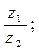 в)
в) 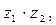 если
если 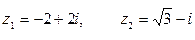 .
.
10. Восемь различных книг расставляются наугад на одной полке. Найдите вероятность того, что две определенные книги окажутся поставленными рядом.
Вариант 9
1.Вычислите пределы функций:
1) 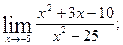 2)
2) 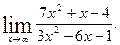
2. Найдите производную функции и вычислите:

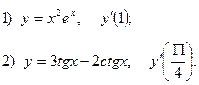
3.Найдите частные производные функции:
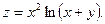
4.Найдите неопределенные интегралы:
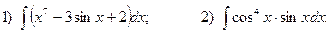
5. Вычислите определенные интегралы:
1) 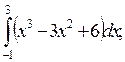 2)
2) 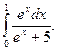
6. Найти общее решение дифференциального уравнения:
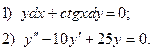
7. Вычислите по формуле трапеций 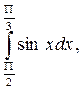 с точностью до 0,001, разбив интервал интегрирования на 6 частей.
с точностью до 0,001, разбив интервал интегрирования на 6 частей.
8. Решить систему уравнений по формулам Крамера:
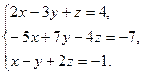
9. Найти а) 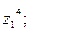 б)
б) 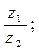 в)
в) 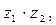 если
если
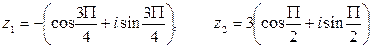 .
.
10. Бросаются одновременно 2 игральные кости. Найдите вероятность следующего события: сумма выпавших очков равна 8.
Вариант 10
1.Вычислите пределы функций:
1) 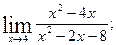 2)
2) 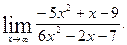
2. Найдите производную функции и вычислите:

3.Найдите частные производные функции:
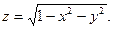
4.Найдите неопределенные интегралы:
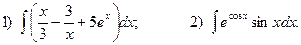
5. Вычислите определенные интегралы:
1) 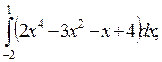 2)
2) 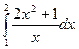
6. Найдите общее решение дифференциального уравнения:
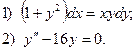
7. Вычислите по формуле прямоугольников 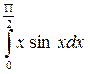 с точностью до 0,0001, разбив интервал интегрирования на 6 частей.
с точностью до 0,0001, разбив интервал интегрирования на 6 частей.
8. Решить систему уравнений методом Гаусса:
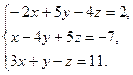
9. Найти а) 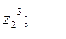 б)
б) 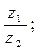 в)
в) 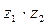 , если
, если 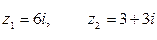
10.
Дискретная случайная величина распределена по закону:
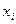
| -1 | 0 | 1 | 2 |
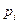
| 0,2 | 0,1 | 0,3 | 0,4 |
Найдите математическое ожидание и дисперсию случайной величины Х.
Вариант 11
1.Вычислите пределы функций:
1) 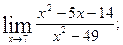 2)
2) 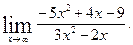
2. Найдите производную функции и вычислите:
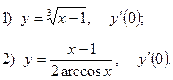
3.Найдите частные производные функции:
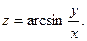
4.Найдите неопределенные интегралы:

5. Вычислите определенные интегралы:
1) 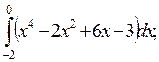 2)
2) 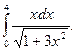
6. Найдите общее решение дифференциального уравнения:
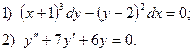
7. Вычислите по формуле прямоугольников 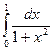 , приняв п=5.
, приняв п=5.
8. Решить систему уравнений по формулам Крамера:
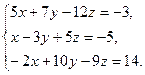
9. Найти а) 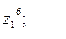 б)
б) 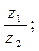 в)
в) 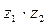 , если
, если
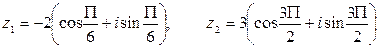 .
.
10. В ящике в случайном порядке разложены 20 деталей, причем 5 из них нестандартные. Рабочий берет наудачу 3 детали. Найти вероятность того, что по крайней мере одна из взятых деталей окажется нестандартной.
Вариант 12
1.Вычислите пределы функций:
1) 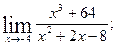 2)
2) 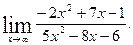
2. Найдите производную функции и вычислите:
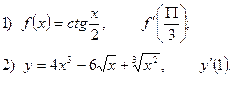
3.Найдите частные производные функции: 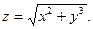
4.Найдите неопределенные интегралы:
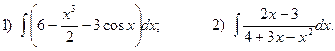
5. Вычислите определенные интегралы:
1) 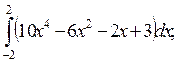 2)
2) 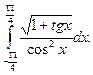
6. Найдите общее решение дифференциального уравнения:
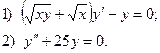
7. Вычислить по формуле прямоугольников 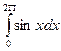 , приняв п = 12.
, приняв п = 12.
8. Решить систему уравнений методом Гаусса:
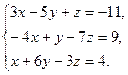
9. Найти а) 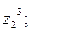 б)
б) 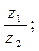 в)
в) 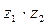 , если
, если 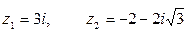 .
.
10. В книжном магазине на полке 10 различных книг, причем 5 книг стоят по 40 рублей каждая; 3 книги – по 10 рублей и 2 книги – по 30 рублей. Найдите вероятность того, что взятые наугад две книги стоят по 50 рублей.
Вариант 13
1.Вычислите пределы функций:
1) 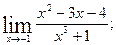 2)
2) 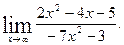
2. Найдите производную функции и вычислите:
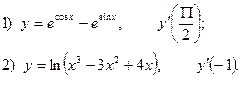
3.Найдите частные производные функции: 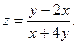
4.Найдите неопределенные интегралы:

5. Вычислите определенные интегралы:
1) 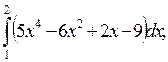 2)
2) 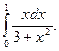
6. Найдите общее решение дифференциального уравнения:
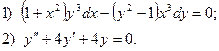
7. Вычислите по формуле трапеций 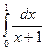 при п = 10 с точностью до 0,0001.
при п = 10 с точностью до 0,0001.
8. Решить систему уравнений по формулам Крамера:
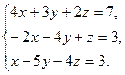
9. Найти а) 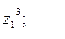 б)
б) 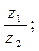 в)
в) 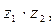 если
если
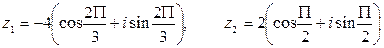 .
.
10. Установите, может ли распределение случайной величины быть задано таблицей:
1)
| 2 | 3 | -4 | 1 | 3/4 |
| 0,3 | 0,1 | 0,2 | 0,3 | 0,2 |
2)
| 5/2 | 4 | 1 | 2 | -3 |
| 0,1 | 0,2 | 0,3 | 0,3 | 0,1 |
Вариант 14
1.Вычислите пределы функций:
1) 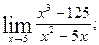 2)
2) 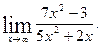
2. Найдите производную функции и вычислите:
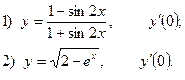
3.Найдите частные производные функции: 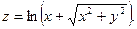
4.Найдите неопределенные интегралы:
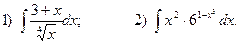
5. Вычислите определенные интегралы:
1) 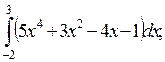 2)
2) 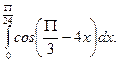
6. Найдите общее решение дифференциального уравнения:
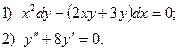
7. Вычислить по формуле трапеций 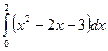 , приняв п = 10.
, приняв п = 10.
8. Решить систему уравнений методом Гаусса:
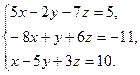
9. Найти а) 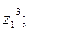 б)
б) 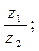 в)
в) 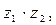 если
если
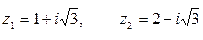 .
.
10. На смотр самодеятельности представлены четыре вокальных номера и художественное чтение. Сколькими способами можно провести смотр?
Вариант 15
1.Вычислите пределы функций:
1) 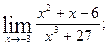 2)
2) 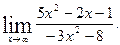
2. Найдите производную функции и вычислите:
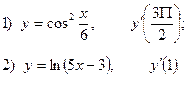
3.Найдите частные производные функции: 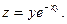
4.Найдите неопределенные интегралы:
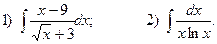
5. Вычислите определенные интегралы:
1) 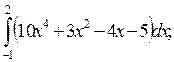 2)
2) 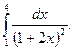
6. Найдите общее решение дифференциального уравнения:
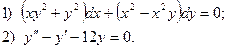
7. Вычислите по формулам прямоугольников интеграл 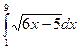 , разбив промежуток интегрирования на 8 равных частей.
, разбив промежуток интегрирования на 8 равных частей.
8. Решить систему уравнений по формулам Крамера:
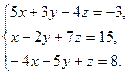
9. Найти а) 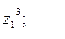 б)
б) 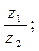 в)
в) 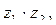 если
если 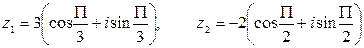 .
.
10. Найдите математическое ожидание и дисперсию случайной величины Х, зная закон ее распределения:
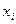
| -1 | 0 | 1 | 2 | 3 |
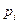
| 0,2 | 0,1 | 0,25 | 0,15 | 0,3 |
Вариант 16
1.Вычислите пределы функций:
1) 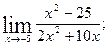 2)
2) 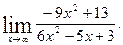
2. Найдите производную функции и вычислите:
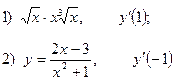
3.Найдите частные производные функции: 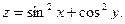
4.Найдите неопределенные интегралы:
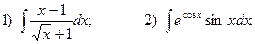
5. Вычислите определенные интегралы:
1) 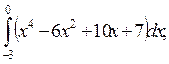 2)
2) 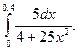
6. Найдите общее решение дифференциального уравнения:
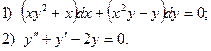
7. Вычислить по формуле прямоугольников интеграл 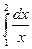 , приняв п = 10 с точностью до 0,001.
, приняв п = 10 с точностью до 0,001.
8. Решить систему уравнений методом Гаусса:
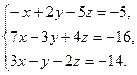
9. Найти а) 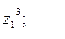 б)
б) 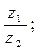 в)
в) 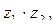 если
если 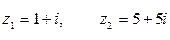 .
.
10. В коробке находятся 250 лампочек, из них 100 по 100Вт, 50 по 60Вт и 50 по 15Вт. Вычислите вероятность того, что мощность любой взятой наугад лампочки не превысит 60Вт.
Вариант 17
1.Вычислите пределы функций:
1) 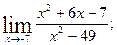 2)
2) 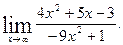
2. Найдите производную функции и вычислите:
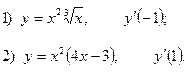
3.Найдите частные производные функции: 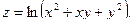
4.Найдите неопределенные интегралы:
1) 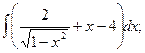 2)
2) 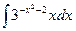
5. Вычислите определенные интегралы:
1) 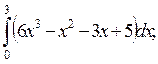 2)
2) 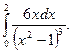
6. Найдите общее решение дифференциального уравнения:
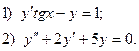
7. Вычислите по формуле трапеций интеграл 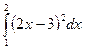 , разбив промежуток интегрирования на 10 равных частей.
, разбив промежуток интегрирования на 10 равных частей.
8. Решить систему уравнений по формулам Крамера:
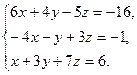
9. Найти а) 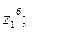 б)
б) 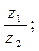 в)
в) 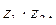 если
если
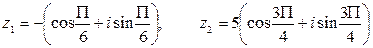 .
.
10. В классе 17 девочек и 14 мальчиков. Определите вероятность того, что оба вызванных ученика окажутся: а) мальчиками; б) девочками.
Вариант 18
1.Вычислите пределы функций:
1) 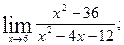 2)
2) 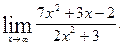
2. Найдите производную функции и вычислите:
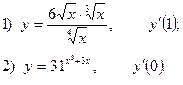
3.Найдите частные производные функции: 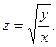
4.Найдите неопределенные интегралы:
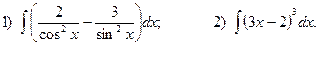
5. Вычислите определенные интегралы:
1) 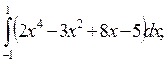 2)
2) 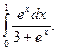
6. Найдите общее решение дифференциального уравнения:
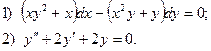
7. Вычислить по формуле прямоугольников интеграл 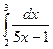 , приняв п = 10 с точностью до 0,001.
, приняв п = 10 с точностью до 0,001.
8. Решить систему уравнений методом Гаусса:
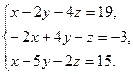
9. Найти а) 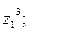 б)
б) 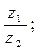 в)
в) 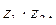 если
если 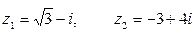 .
.
10. Из букв составлено слово «книга». Это слово рассыпали и произвольно собрали заново. Какова вероятность того, что снова получится слово «книга»?
Вариант 19
1.Вычислите пределы функций:
1) 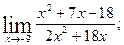 2)
2) 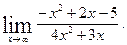
2. Найдите производную функции и вычислите:
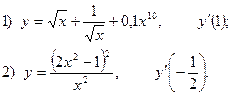
3.Найдите частные производные функции: 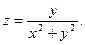
4.Найдите неопределенные интегралы:
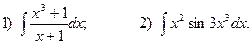
5. Вычислите определенные интегралы:
1) 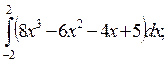 2)
2) 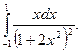
6. Найдите общее решение дифференциального уравнения:
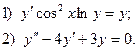
7. Вычислите по формуле трапеций интеграл 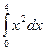 , разбив промежуток интегрирования на 10 равных частей.
, разбив промежуток интегрирования на 10 равных частей.
8. Решить систему уравнений по формулам Крамера:
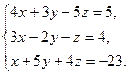
9. Найти а) 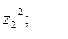 б)
б) 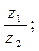 в)
в) 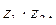 если
если
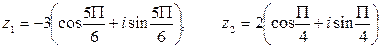 .
.
10. В семизначном телефонном номере забыта последняя цифра. Определите вероятность того, что наугад выбранная цифра окажется верной.
Вариант 20
1.Вычислите пределы функций:
1) 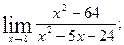 2)
2) 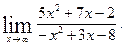
2. Найдите производную функции и вычислите:
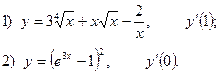
3.Найдите частные производные функции: 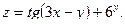
4.Найдите неопределенные интегралы:
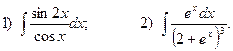
5. Вычислите определенные интегралы:
1) 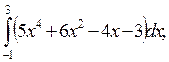 2)
2) 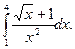
6. Найдите общее решение дифференциального уравнения:
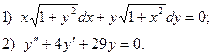
7. Вычислить по формуле трапеций интеграл 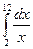 , приняв п = 10 с точностью до 0,001.
, приняв п = 10 с точностью до 0,001.
8. Решить систему уравнений методом Гаусса:
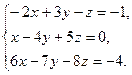
9. Найти а) 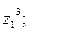 б)
б) 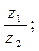 в)
в) 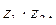 если
если 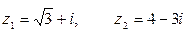 .
.
10. В урне 4 красных и 7 синих шаров. Из урны одновременно вынимают два шара. Какова вероятность того, что оба шара красные?
Вариант 21
1.Вычислите пределы функций:
1) 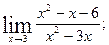 2)
2) 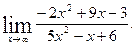
2. Найдите производную функции и вычислите:
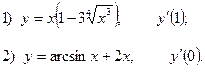
3.Найдите частные производные функции: 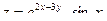
4.Найдите неопределенные интегралы:
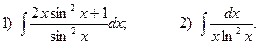
5. Вычислите определенные интегралы:
1) 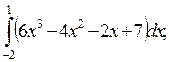 2)
2) 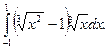
6. Найдите общее решение дифференциального уравнения:
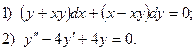
7. Вычислите по формуле трапеций интеграл 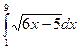 , разбив промежуток интегрирования на 8 равных частей.
, разбив промежуток интегрирования на 8 равных частей.
8. Решить систему уравнений по формулам Крамера:
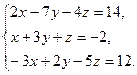
9. Найти а) 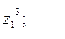 б)
б) 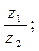 в)
в) 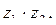 если
если
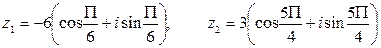 .
.
10. В лотерее из 100 билетов имеются 5 выигрышей по 300 рублей, 10 выигрышей по 200 рублей и 55 выигрышей по 100 рублей. Какова вероятность на один купленный билет выиграть не менее 200 рублей?
Вариант 22
1.Вычислите пределы функций:
1) 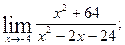 2)
2) 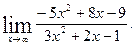
2. Найдите производную функции и вычислите:
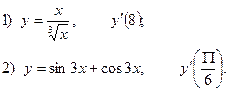
3.Найдите частные производные функции: 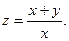
4.Найдите неопределенные интегралы:
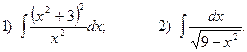
5. Вычислите определенные интегралы:
1) 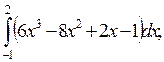 2)
2) 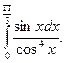
6. Найти общее решение дифференциального уравнения:
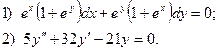
7. Вычислить по формуле трапеций интеграл 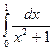 , приняв п = 10 с точностью до 0,001.
, приняв п = 10 с точностью до 0,001.
8. Решить систему уравнений методом Гаусса:
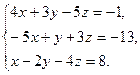
9. Найти а) 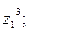 б)
б) 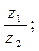 в)
в) 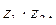 если
если 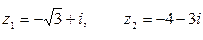 .
.
10. Правильная треугольная пирамида имеет пронумерованные грани 1, 2, 3, 4. Запишите закон распределения для выпадения номера грани, на которой стоит пирамида и вычислите математическое ожидание.
Вариант 23
1.Вычислите пределы функций:
1) 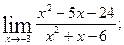 2)
2) 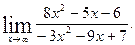
2. Найдите производную функции и вычислите:
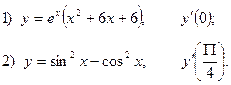
3.Найдите частные производные функции: 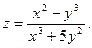
4.Найдите неопределенные интегралы:

5. Вычислите определенные интегралы:
1) 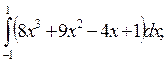 2)
2) 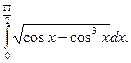
6. Найдите общее решение дифференциального уравнения:
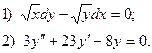
7. Вычислите по формуле прямоугольников интеграл 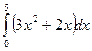 , разбив промежуток интегрирования на 10 равных частей.
, разбив промежуток интегрирования на 10 равных частей.
8. Решить систему уравнений по формулам Крамера:
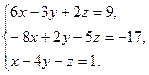
9. Найти а) 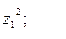 б)
б) 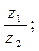 в)
в) 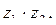 если
если
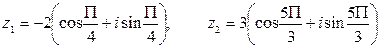 .
.
10. Собрание сочинений из четырех томов нужно поставить на полку по порядку. Вычислите вероятность того, что нужный порядок будет достигнут.
Вариант 24
1.Вычислите пределы функций:
1) 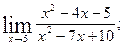 2)
2) 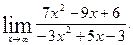
2. Найдите производную функции и вычислите:
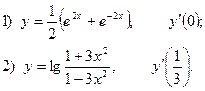
3.Найдите частные производные функции: 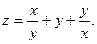
4.Найдите неопределенные интегралы:
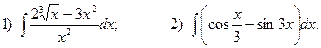
5. Вычислите определенные интегралы:
1) 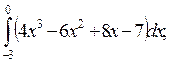 2)
2) 
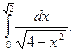
6. Найти общее решение дифференциального уравнения:
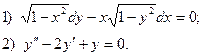
7. Вычислить по формуле прямоугольников интеграл 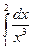 , приняв п = 10 с точностью до 0,001.
, приняв п = 10 с точностью до 0,001.
8. Решить систему уравнений методом Гаусса:
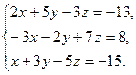
9. Найти а) 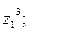 б)
б) 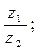 в)
в) 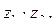 если
если 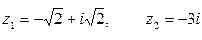 .
.
10. При перевозке ящика, в котором содержались 21 стандартная и 10 нестандартных деталей, утеряна одна деталь, причем неизвестно какая. Найдите вероятность того, что была утеряна: а) стандартная деталь; б) нестандартная деталь.
Вариант 25
1.Вычислите пределы функций:
1) 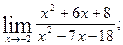 2)
2) 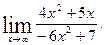
2. Найдите производную функции и вычислите:
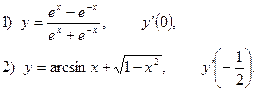
3.Найдите частные производные функции: 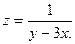
4.Найдите неопределенные интегралы:
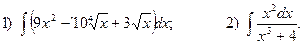
5. Вычислите определенные интегралы:
1) 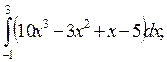 2)
2) 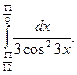
6. Найти общее решение дифференциального уравнения:
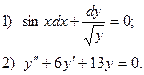
7. Вычислите по формуле трапеций интеграл 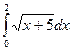 , разбив промежуток интегрирования на 10 равных частей.
, разбив промежуток интегрирования на 10 равных частей.
8. Решить систему уравнений по формулам Крамера:
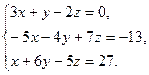
9. Найти а) 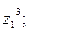 б)
б) 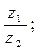 в)
в) 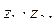 если
если
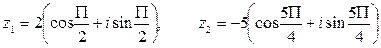 .
.
10. Найдите математическое ожидание и дисперсию дискретной случайной величины Х, заданной законом распределения:
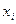
| -5 | 2 | 3 | 4 |
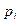
| 0,4 | 0,3 | 0,1 | 0,2 |
Вариант 26
1.Вычислите пределы функций:
1) 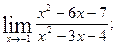 1)
1) 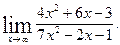
2. Найдите производную функции и вычислите:
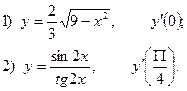
3.Найдите частные производные функции: 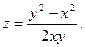
4.Найдите неопределенные интегралы:
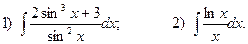
5. Вычислите определенные интегралы:
1) 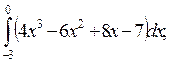 2)
2) 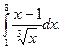

6. Найдите общее решение дифференциального уравнения:
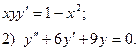
7. Вычислить по формуле прямоугольников интеграл 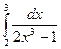 , приняв п = 10 с точностью до 0,001.
, приняв п = 10 с точностью до 0,001.
8. Решить систему уравнений методом Гаусса:
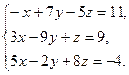
9. Найти а) 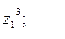 б)
б) 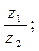 в)
в) 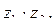 если
если 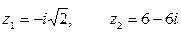 .
.
10. Случайная величина задана следующим рядом распределения:
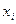
| 2 | 4 | 7 | 10 | 12 |
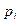
| 0,1 | 0,2 | 0,4 | 0,2 | 0,1 |
Определите математическое ожидание и дисперсию.
Вариант 27
1.Вычислите пределы функций:
1) 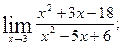 2)
2) 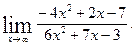
2. Найдите производную функции и вычислите:
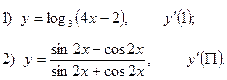
3.Найдите частные производные функции: 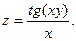
4.Найдите неопределенные интегралы:

5. Вычислите определенные интегралы:
1) 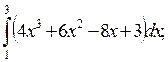 2)
2) 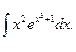
6. Найти общее решение дифференциального уравнения:
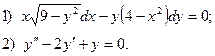
7. Вычислите по формуле трапеций интеграл 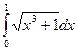 , разбив промежуток интегрирования на 8 равных частей.
, разбив промежуток интегрирования на 8 равных частей.
8. Решить систему уравнений по формулам Крамера:
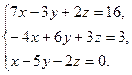
9. Найти а) 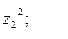 б)
б) 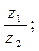 в)
в) 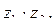 если
если
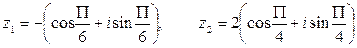 .
.
10. В розыгрыше первенства по шахматам было сыграно 120 игр. Сколько было участников, если каждые два участника встречались между собой один раз?
Вариант 28
1.Вычислите пределы функций:
1) 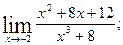 2)
2) 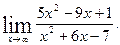
2. Найдите производную функции и вычислите:
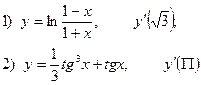
3.Найдите частные производные функции: 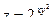
4.Найдите неопределенные интегралы:
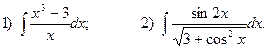
5. Вычислите определенные интегралы:
1) 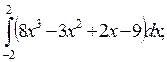 2)
2) 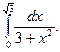

6. Найдите общее решение дифференциального уравнения:
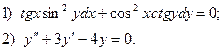
7. Вычислить по формуле трапеций интеграл 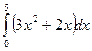 , приняв п = 10 с точностью до 0,001.
, приняв п = 10 с точностью до 0,001.
8. Решить систему уравнений методом Гаусса:
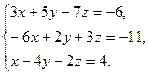
9. Найти а) 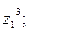 б)
б) 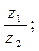 в)
в) 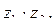 если
если 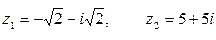 .
.
10. От коллектива бригады, которая состоит из 6 мужчин и 4 женщин, на профсоюзную конференцию выбираются два человека. Какова вероятность, что среди выбранных хотя бы одна женщина?
Вариант 29
1.Вычислите пределы функций:
1) 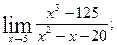 2)
2) 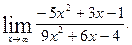
2. Найдите производную функции и вычислите:
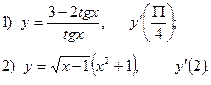
3.Найдите частные производные функции: 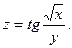
4.Найдите неопределенные интегралы:
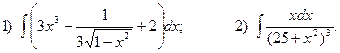
5. Вычислите определенные интегралы:
1) 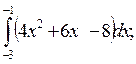 2)
2) 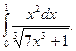
6. Найдите общее решение дифференциального уравнения:
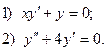
7. Вычислите по формуле прямоугольников интеграл 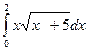 , разбив промежуток интегрирования на 10 равных частей.
, разбив промежуток интегрирования на 10 равных частей.
8. Решить систему уравнений по формулам Крамера:
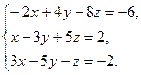
9. Найти а) 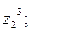 б)
б) 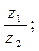 в)
в) 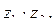 если
если
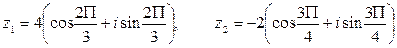 .
.
10. В партии из восьми деталей пять стандартных. Наудачу взяты четыре детали. Какова вероятность, что среди отобранных деталей окажется три стандартных детали?
Вариант 30
1.Вычислите пределы функций:
1) 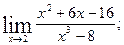 2)
2) 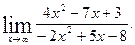
2. Найдите производную функции и вычислите:
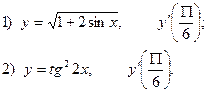
3.Найдите частные производные функции: 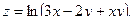
4.Найдите неопределенные интегралы:
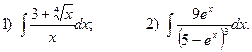
5. Вычислите определенные интегралы:
1) 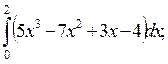 2)
2) 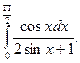

6. Найдите общее решение дифференциального уравнения:
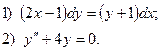
7. Вычислить по формуле прямоугольников интеграл 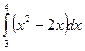 , приняв п = 10 с точностью до 0,001.
, приняв п = 10 с точностью до 0,001.
8. Решить систему уравнений методом Гаусса:
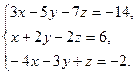
9. Найти а) 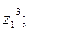 б)
б) 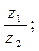 в)
в) 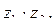 если
если 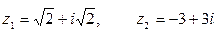 .
.
10. Сколько шестизначных чисел можно составить из цифр 0,1,2,3,4,5, не повторяя цифр в числе?
Перечень рекомендуемых учебных изданий, Интернет-ресурсов, дополнительной литературы
Основные источники:
1. Математика: учеб. Пособие/В.П. Омельченко, Э.В. Курбатова. – Изд. 6-е, стер. – Ростов н/Д: Феникс, 2012. – 380с. – (Среднее профессиональное образование.
2. Математика: учебник для студентов образовательных учреждений среднего профессионального образования/ И.Д. Пехлецкий. – 6-е изд., стер. – М.: Издательский центр «Академия», 2010. – 304 с.
3. Сборник задач по математике/А.А. Дадаян. М.: ФОРУМ: ИНФРА-М, 2005. – 352 с. (Профессиональное образование).
Дополнительные источники:
1. Сборник задач по математике с решениями для техникумов/ И.Л. Соловейчик, В.Т. Лисичкин. – М.: ООО «Издательский дом ОНИКС 21 век»: ООО «Издательство «Мир и Образование», 2003. – 464 с.: ил.
Дата: 2018-11-18, просмотров: 413.