Расширение понятия уравнения. Понятие о дифференциальном уравнении. Задачи, приводящие к дифференциальным уравнениям. Порядок дифференциального уравнения. Дифференциальные уравнения с разделяющимися переменными. Задача Коши для дифференциального уравнения с разделяющимися переменными.

Понятие о дифференциальном уравнении высшего порядка. Дифференциальное уравнение второго порядка и его общее решение. Линейные уравнения второго порядка с постоянными коэффициентами. Задача Коши для дифференциального уравнения второго порядка с постоянными коэффициентами.   

Методические указания

Дифференциальным уравнением называется равенство, содержащее производные или дифференциалы неизвестной функции.

Общий вид дифференциального уравнения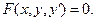

Функция, удовлетворяющая дифференциальному уравнению, т.е. обращающая его в тождество, называется интегралом или решением этого уравнения.

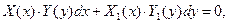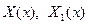1. Дифференциальным уравнением с разделяющимися переменными называется уравнение вида  где  функции только от х,  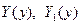функции только от у.

Делением данного уравнения на 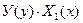, получим уравнение с разделяющимися переменными: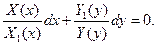

Общий интеграл (решение) данного уравнения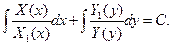

Задача нахождения решения дифференциального уравнения, удовлетворяющего условию 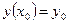, где 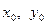 - заданные числа, называется задачей Коши.

Геометрический смысл решения задачи Коши заключается в нахождении интегральной кривой, проходящей через заданную точку М(х₀;у₀).

Пример 1.

Найти общее решение уравнения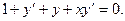

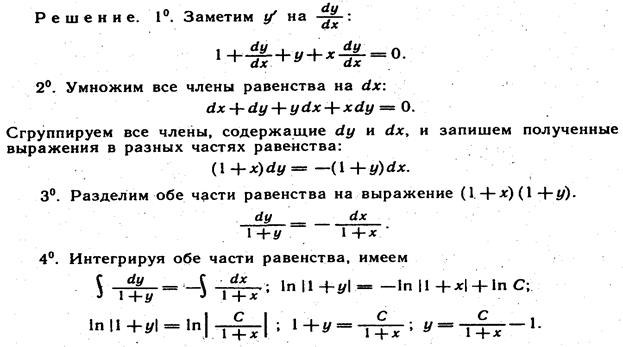
2. Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида 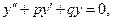 где p, q – постоянные величины.

Уравнение 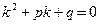 называется характеристическим уравнением для данного дифференциального уравнения. Чтобы получить это уравнение, достаточно заменить 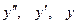соответственно на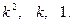

Общим решением дифференциального уравнения второго порядка называется функция y=g(x, С₁, С₂₎  от х и двух произвольных постоянных С₁ и С₂.

Задача Коши для дифференциального уравнения второго порядка состоит в том, чтобы найти решение, удовлетворяющее начальным условиям у(х₀)=у₀, у¹(х₀)=у₀¹.

Постоянные С₁ и С₂ определяются из системы соответствующих уравнений.        При решении характеристического уравнения возможны три случая:

№	Корни уравнения	Частные решения	Общее решение
1	D>0, действительные, k1, k2 - различные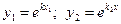
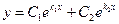
2	D=0, действительные, k1=k2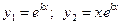
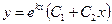
3	D<0, комплексно-сопряженные,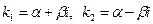

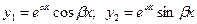
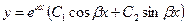
Пример 1. Найти общее решение дифференциального уравнения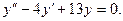

Пример 2. Найти частное решение дифференциального уравнения 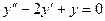, удовлетворяющее начальным условиям при х=0, у₀=4,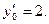

Тема 1.5. Численные методы

Приближенное вычисление определенных интегралов с помощью формул прямоугольников, трапеций, парабол.

Методические указания

1. Чтобы найти приближенное значение интеграла 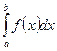методом прямоугольников, нужно:

1) разделить отрезок интегрирования [a ; b] на п равных частей точками х₀=а, х₁, х₂, …, х_п-1, х_п= b ;

2) вычислить значения подынтегральной функции y = f ( x ) в полученных точках: y ₀ = f ( x ₀ ), y ₁ = f ( x ₁ ), y ₂ = f ( x ₂ ), …, y_{n -1} = f ( x_{n -1} ), y_n = y ( x_n );

3) воспользоваться формулой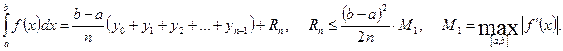

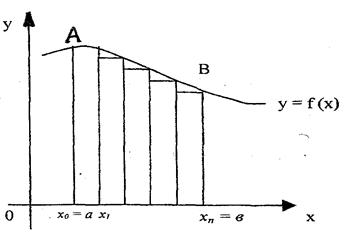
2. Чтобы найти приближенное значение интеграла 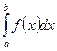методом трапеций, нужно:

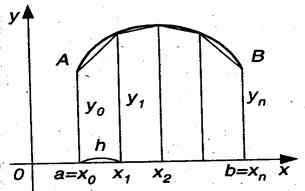
1) разделить отрезок интегрирования [a ; b] на п равных частей точками х₀=а, х₁, х₂, …, х_п-1, х_п= b ;

2) вычислить значения подынтегральной функции y = f ( x ) в полученных точках: y ₀ = f ( x ₀ ), y ₁ = f ( x ₁ ), y ₂ = f ( x ₂ ), …, y_{n -1} = f ( x_{n -1} ), y_n = y ( x_n );

3) воспользоваться формулой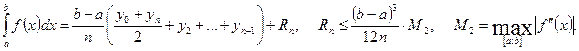

Пример 1.