МАТЕМАТИКА
Программа, методические рекомендации и контрольные задания для обучающихся по заочной форме обучения по специальностям:
21.02.01 (131018) Разработка и эксплуатация нефтяных и газовых месторождений;
21.02.02 (131003) Бурение нефтяных и газовых скважин;
15.02.01 (151031) Монтаж и техническая эксплуатация промышленного оборудования (по отраслям)
2013
Методические указания составлены в соответствии с ФГОС СПО по специальностям: 131018 Разработка и эксплуатация нефтяных и газовых месторождений, 131003 Бурение нефтяных и газовых скважин, 151031 Монтаж и техническая эксплуатация промышленного оборудования (по отраслям).
Утверждено
Зам.директора по УР: А.П.Шаповалов
«29» ноября 2013г.
Организация-разработчик: ГБОУ СПО «ЖНТ»
Разработчик: Дербенева Г.С., старший методист
Рецензенты:
О.В. Олейникова, зам председателя районного отдела образования, куратор дисциплин Математика, Физика, Информатика
Р.Г. Покрепина, преподаватель ГБОУ СПО «ЖНТ»
Рассмотрена на заседании цикловой комиссии естественно-научных дисциплин и информатизации
Протокол № 8 от «05» апреля 2013 г.
Рекомендована Методическим советом техникума
Протокол № 8 от «26» июня 2013 г.
Допущено учебно-методическим объединением Совета директоров средних специальных учебных заведений Волгоградской области в качестве учебного пособия для образовательных учреждений среднего профессионального образования Волгоградской области
Протокол №19 от 18.11.2013г.
Содержание
1. Пояснительная записка . . . . . … …… ……. . . . . . . . . . . . . . . . . . . .
2. Требования к выполнению и оформлению контрольной работы…. .
3. Тематический план . . . . . . … . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4. Содержание учебной дисциплины и методические указания . . . . . . .
5. Задания для контрольной работы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6. Перечень рекомендуемой литературы для изучения . . . . . . . . . . . . . . .
Пояснительная записка
Методические указания составлены в соответствии с ФГОС СПО по специальностям 131018 Разработка и эксплуатация нефтяных и газовых месторождений, 131003 Бурение нефтяных и газовых скважин, 151031 Монтаж и техническая эксплуатация промышленного оборудования (по отраслям).
В процессе изучения дисциплины обучающиеся должны усвоить основные понятия, утверждения и методы, изложенные в рабочей программе.
Основная задача дисциплины состоит в том, чтобы дать обучающимся комплекс математических знаний, умений и навыков, необходимых для изучения смежных общепрофессиональных дисциплин и модулей.
В соответствии с требованиями ФГОС СПО в области математики
обучающийся должен
уметь:
· анализировать сложные функции и строить их графики;
· выполнять действия над комплексными числами;
· вычислять значения геометрических величин;
· производить операции над матрицами и определителями;
· решать задачи на вычисление вероятности с использованием элементов комбинаторики;
· решать прикладные задачи с использованием элементов дифференциального и интегрального исчислений;
· решать системы линейных уравнений различными методами.
знать:
· основные математические методы решения прикладных задач;
· основные понятия и методы математического анализа, линейной алгебры, теорию комплексных чисел, теории вероятностей и математической статистики;
· основы интегрального и дифференциального исчисления;
· роль и место математики в современном мире при освоении профессиональных дисциплин и в сфере профессиональной деятельности.
В результате изучения вариативной части обучающийся должен по дисциплине «Математика»:
Уметь:
- пользоваться математическими формулами при расчете физических и геометрических величин, применяемых в профессиональной деятельности;
знать:
- правила вычисления числовых выражений.
Итогом изучения дисциплины является сдача экзамена после успешного выполнения практических работ и домашней контрольной работы.
Практические работы снабжены методическими указаниями и примерами выполнения заданий.
Практические работы выполняются в тетради и сдаются в учебную часть заочного отделения для проверки. Зачтенные работы являются допуском к сдаче контрольной работы. Практические работы и контрольная работа оцениваются «зачтено» или «незачтено».
При дистанционной форме обучения обучающиеся сдают экзамен в программе «Прометей». Допуском к сдаче экзамена является успешная сдача тестового контроля.
При традиционной заочной форме обучения обучающиеся во время лабораторно-экзаменационной сессии сдают письменный экзамен.
2. Требования к выполнению и оформлению контрольной работы
1. Задания контрольной работы разработаны в 30-ти вариантах. Вариант определяется по двум последним цифрам шифра обучающегося, например: шифр 08 – вариант №8; шифр 23 – вариант №23. Если шифр более 30, из него следует вычесть 30-ть и по остатку определить вариант. Например: шифр 46, тогда 46-30 = 16, вариант №16; шифр 125 (125-30х4=5), вариант №5.
2. Работа выполняется в отдельной тетради школьного формата или на листах А4. Следует пронумеровать листы и оставить на них поля не менее 3см для замечаний преподавателя.
3. На обложке должен быть приклеен титульный лист установленного образца.
4. Работа должна быть выполнена чернилами одного цвета, аккуратно и разборчиво. Допускается оформление решения на компьютере.
5. Решение заданий должны располагаться в порядке номеров, указанных в задании, номера заданий следует указывать перед условием.
6. Условия заданий должны быть переписаны.
7. Решения заданий должны сопровождаться краткими, но достаточно обоснованными пояснениями, используемые формулы нужно выписывать.
8. В конце работы следует указать литературу, которой вы пользовались.
9. Работа, выполненная не по своему варианту, не учитывается и возвращается студенту без оценки.
ТЕМАТИЧЕСКИЙ ПЛАН
Наименование разделов и тем
Заочная форма обучения
Всего аудит. часов
Тема 1.1. Функции
Понятие элементарной и сложной функции. Предел функции в точке и на бесконечности. Непрерывность функций. Асимптотическое поведение функции.
Методические указания
Определение 1. Число А называется пределом функции f ( x ) при х стремящемся к х0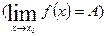 
, если для любого числа 
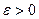существует число 
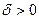, такое, что для всех 
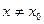из условия 
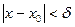следует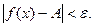 
Определение 2. Число b называется пределом функции y = f ( x ) на бесконечности, если для всякого числа 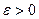можно найти такое число 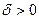, что 
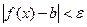, когда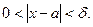 
Определение 3. Число А называется пределом функции y = f ( x ), если для всех достаточно больших по модулю значений аргумента х соответствующие значения функции f ( x ) сколь угодно мало отличаются от числа А.
Теоремы о пределах
Теорема 1. Если существуют пределы функций f ( x ) и g ( x), то существует также и предел их суммы, равный сумме пределов функций f ( x ) и g ( x):
.
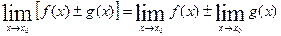Теорема 2. Если существуют пределы функций f ( x ) и g ( x), то существует также и предел их произведения, равный произведению пределов функций f ( x ) и g ( x):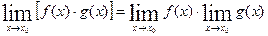 
.
Теорема 3. Если существуют пределы функций f ( x ) и g ( x) и предел функции f ( x ) отличен от нуля, то существует также предел отношения f ( x )/ g ( x), равный отношению пределов функций f ( x ) и g ( x ):
.
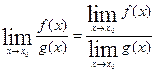Следствия. 1. Постоянный множитель можно вынести за знак предела:
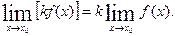
2. Если п— натуральное число, то 
3. Предел многочлена (целой рациональной функци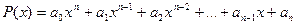и) 
при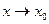 
равен значению этого многочлена при х=х0, т.е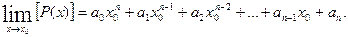 
4. Предел дробно-рациональной функци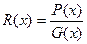и 
при 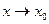равен значению этой функции при х=х0, если х0 принадлежит области определения функции, т.е.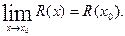 
Правила вычисления пределов
1. При раскрытии неопределенности вида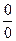 
, необходимо разложить числитель и знаменатель на множители, чтобы сократить дробь на общий множитель, стремящийся к нулю, и, следовательно, сделать возможным применение теоремы о пределе частного двух функций.
2. При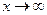 
после применения теоремы о пределе частного двух функций получаем неопределенность вида 
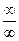. Для ее раскрытия нужно разделить числитель и знаменатель на высшую степень переменной х. Воспользуйтесь наряду с теоремами о пределах и следствиями из них правилом 
.
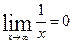Пример 1. Найти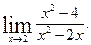 
Решение. Здесь имеем неопределенность типа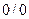 
. Для того, чтобы раскрыть эту неопределенность, разложим числитель и знаменатель дроби на множители и до перехода к пределу сократим дробь на множитель х – 2. В результате получим
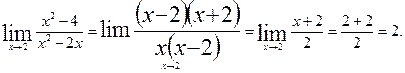Ответ: 2.
Пример 2. Найти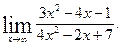 
Решение. Здесь имеем неопределенность типа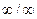 
. Для того, чтобы раскрыть эту неопределенность, разделим числитель и знаменатель дроби на х2. В результате получим
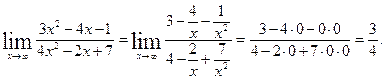Ответ: 0,75.
Пример 1.
Найти производную функции
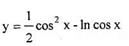
Решение.
Это сложная функция с промежуточным аргументом cos x. Применяя правила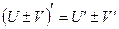 
и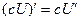 
и формулы 
, 
, 
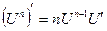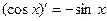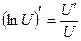, получим:
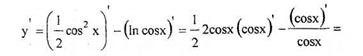
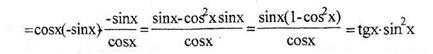
Пример 2.
Найдите частные производные функции
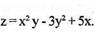
Решение:
Рассматривая у как постоянную величину, находим
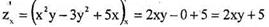
Аналогично, рассматривая х как
постоянную, получим
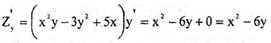
Пример 1.
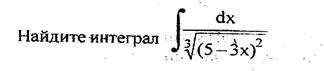
Решение:
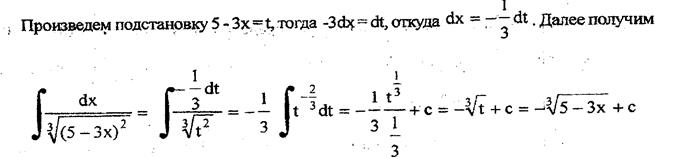
Определенный интеграл
1. Для любой функции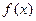 
непрерывной на отрезке 
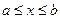, всегда существует определенный интеграл 
.
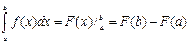2. Свойства определенного интеграла:
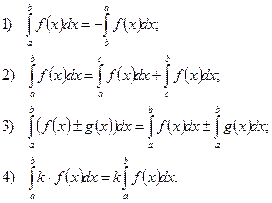
Пример 1.
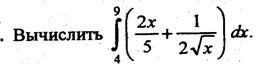
Решение:
На основании свойств 3 и 4 и формулы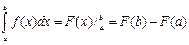 
, получим
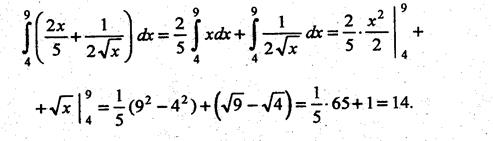
Пример 2.
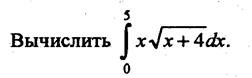
Тема 1.5. Численные методы
Приближенное вычисление определенных интегралов с помощью формул прямоугольников, трапеций, парабол.
Методические указания
1. Чтобы найти приближенное значение интеграла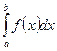 
методом прямоугольников, нужно:
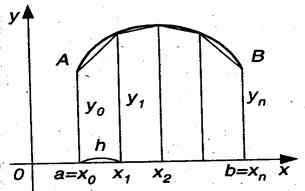
1) разделить отрезок интегрирования [a ; b] на п равных частей точками х0=а, х1, х2, …, хп-1, хп= b ;
2) вычислить значения подынтегральной функции y = f ( x ) в полученных точках: y 0 = f ( x 0 ), y 1 = f ( x 1 ), y 2 = f ( x 2 ), …, yn -1 = f ( xn -1 ), yn = y ( xn );
3) воспользоваться формулой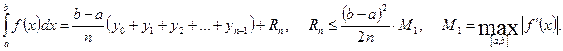 
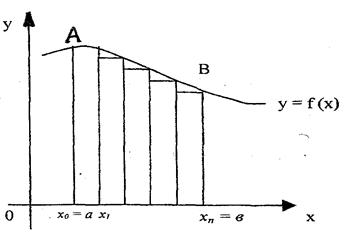
2. Чтобы найти приближенное значение интеграла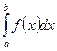 
методом трапеций, нужно:
1) разделить отрезок интегрирования [a ; b] на п равных частей точками х0=а, х1, х2, …, хп-1, хп= b ;
2) вычислить значения подынтегральной функции y = f ( x ) в полученных точках: y 0 = f ( x 0 ), y 1 = f ( x 1 ), y 2 = f ( x 2 ), …, yn -1 = f ( xn -1 ), yn = y ( xn );
3) воспользоваться формулой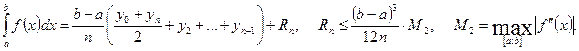 
Пример 1. 
Понятие мнимой единицы
Степени мнимой единицы
Тема 4.1. Основные понятия комбинаторики
МАТЕМАТИКА
Программа, методические рекомендации и контрольные задания для обучающихся по заочной форме обучения по специальностям:
21.02.01 (131018) Разработка и эксплуатация нефтяных и газовых месторождений;
21.02.02 (131003) Бурение нефтяных и газовых скважин;
15.02.01 (151031) Монтаж и техническая эксплуатация промышленного оборудования (по отраслям)
2013
Методические указания составлены в соответствии с ФГОС СПО по специальностям: 131018 Разработка и эксплуатация нефтяных и газовых месторождений, 131003 Бурение нефтяных и газовых скважин, 151031 Монтаж и техническая эксплуатация промышленного оборудования (по отраслям).
Утверждено
Зам.директора по УР: А.П.Шаповалов
«29» ноября 2013г.
Организация-разработчик: ГБОУ СПО «ЖНТ»
Разработчик: Дербенева Г.С., старший методист
Рецензенты:
О.В. Олейникова, зам председателя районного отдела образования, куратор дисциплин Математика, Физика, Информатика
Р.Г. Покрепина, преподаватель ГБОУ СПО «ЖНТ»
Рассмотрена на заседании цикловой комиссии естественно-научных дисциплин и информатизации
Протокол № 8 от «05» апреля 2013 г.
Рекомендована Методическим советом техникума
Протокол № 8 от «26» июня 2013 г.
Допущено учебно-методическим объединением Совета директоров средних специальных учебных заведений Волгоградской области в качестве учебного пособия для образовательных учреждений среднего профессионального образования Волгоградской области
Протокол №19 от 18.11.2013г.
Содержание
1. Пояснительная записка . . . . . … …… ……. . . . . . . . . . . . . . . . . . . .
2. Требования к выполнению и оформлению контрольной работы…. .
3. Тематический план . . . . . . … . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4. Содержание учебной дисциплины и методические указания . . . . . . .
5. Задания для контрольной работы . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6. Перечень рекомендуемой литературы для изучения . . . . . . . . . . . . . . .
Пояснительная записка
Методические указания составлены в соответствии с ФГОС СПО по специальностям 131018 Разработка и эксплуатация нефтяных и газовых месторождений, 131003 Бурение нефтяных и газовых скважин, 151031 Монтаж и техническая эксплуатация промышленного оборудования (по отраслям).
В процессе изучения дисциплины обучающиеся должны усвоить основные понятия, утверждения и методы, изложенные в рабочей программе.
Основная задача дисциплины состоит в том, чтобы дать обучающимся комплекс математических знаний, умений и навыков, необходимых для изучения смежных общепрофессиональных дисциплин и модулей.
В соответствии с требованиями ФГОС СПО в области математики
обучающийся должен
уметь:
· анализировать сложные функции и строить их графики;
· выполнять действия над комплексными числами;
· вычислять значения геометрических величин;
· производить операции над матрицами и определителями;
· решать задачи на вычисление вероятности с использованием элементов комбинаторики;
· решать прикладные задачи с использованием элементов дифференциального и интегрального исчислений;
· решать системы линейных уравнений различными методами.
знать:
· основные математические методы решения прикладных задач;
· основные понятия и методы математического анализа, линейной алгебры, теорию комплексных чисел, теории вероятностей и математической статистики;
· основы интегрального и дифференциального исчисления;
· роль и место математики в современном мире при освоении профессиональных дисциплин и в сфере профессиональной деятельности.
В результате изучения вариативной части обучающийся должен по дисциплине «Математика»:
Уметь:
- пользоваться математическими формулами при расчете физических и геометрических величин, применяемых в профессиональной деятельности;
знать:
- правила вычисления числовых выражений.
Итогом изучения дисциплины является сдача экзамена после успешного выполнения практических работ и домашней контрольной работы.
Практические работы снабжены методическими указаниями и примерами выполнения заданий.
Практические работы выполняются в тетради и сдаются в учебную часть заочного отделения для проверки. Зачтенные работы являются допуском к сдаче контрольной работы. Практические работы и контрольная работа оцениваются «зачтено» или «незачтено».
При дистанционной форме обучения обучающиеся сдают экзамен в программе «Прометей». Допуском к сдаче экзамена является успешная сдача тестового контроля.
При традиционной заочной форме обучения обучающиеся во время лабораторно-экзаменационной сессии сдают письменный экзамен.
2. Требования к выполнению и оформлению контрольной работы
1. Задания контрольной работы разработаны в 30-ти вариантах. Вариант определяется по двум последним цифрам шифра обучающегося, например: шифр 08 – вариант №8; шифр 23 – вариант №23. Если шифр более 30, из него следует вычесть 30-ть и по остатку определить вариант. Например: шифр 46, тогда 46-30 = 16, вариант №16; шифр 125 (125-30х4=5), вариант №5.
2. Работа выполняется в отдельной тетради школьного формата или на листах А4. Следует пронумеровать листы и оставить на них поля не менее 3см для замечаний преподавателя.
3. На обложке должен быть приклеен титульный лист установленного образца.
4. Работа должна быть выполнена чернилами одного цвета, аккуратно и разборчиво. Допускается оформление решения на компьютере.
5. Решение заданий должны располагаться в порядке номеров, указанных в задании, номера заданий следует указывать перед условием.
6. Условия заданий должны быть переписаны.
7. Решения заданий должны сопровождаться краткими, но достаточно обоснованными пояснениями, используемые формулы нужно выписывать.
8. В конце работы следует указать литературу, которой вы пользовались.
9. Работа, выполненная не по своему варианту, не учитывается и возвращается студенту без оценки.
ТЕМАТИЧЕСКИЙ ПЛАН
Наименование разделов и тем
Макс. уч. нагрузка обучающегося, час
Дата: 2018-11-18, просмотров: 317.
