В ходе анализа финансового состояния коммерческой организации используется ряд стандартных приемов чтения финансовой отчетности, основными из которых являются следующие:
- горизонтальный анализ;
- вертикальный анализ;
- трендовый анализ;
- расчет финансовых коэффициентов;
- факторный анализ.
Целью горизонтального анализа является сопоставление абсолютных показателей бухгалтерской отчетности и выявление их изменений за анализируемый период. Таким образом, в рамках горизонтального анализа реализуется такой универсальный прием общего анализа, как «сравнение».
Вертикальный анализ позволяет отобразить структуру обобщающего финансового показателя в виде относительных величин, в качестве которых выступают «удельные веса». Они рассчитываются как отношение элемента в составе обобщающего показателя к величине самого обобщающего показателя, выраженное в процентной форме. С помощью показателей структуры дается обоснованная оценка изменений в составе финансовых ресурсов и имущества, сформированного с их помощью. Кроме того, относительные величины структуры сглаживают негативное влияние инфляционных процессов. В ходе анализа финансового состояния вертикальный анализ используется при формировании оценки структуры имущества и финансовых ресурсов.
Целью трендового анализа является определение основной тенденции изменения показателей в динамике. В ходе трендового анализа наличия и размещения финансовых ресурсов темп роста рассчитывается как отношение абсолютного значения финансового показателя на конец анализируемого периода к значению этого показателя на начало того же периода, выраженное в процентах. При анализе деловой активности используются относительные величины динамики основных оценочных показателей деятельности организации в виде темпов роста, рассчитанных как отношение фактического значения показателя в отчетном периоде к фактическому значению этого же показателя в предшествующем, выраженное в процентах.
В ходе анализа таких сторон финансового состояния, как деловая активность, финансовая устойчивость, платежеспособность, широко используются финансовые коэффициенты. Они рассчитываются как отношение абсолютного значения одного финансового показателя к абсолютному значению другого и позволяют дать количественную характеристику изучаемой стороны финансового состояния.
В ходе анализа финансового состояния решаются задачи как прямого, так и обратного факторного анализа.
В задачах прямого факторного анализа рассчитывается влияние отдельных факторов, обусловливающих изменение основных оценочных показателей деятельности организации (выручки, прибыли), средней величины используемого оборотного капитала и финансовых коэффициентов.
Основным приемом изучения прямой детерминированной факторной связи выступает метод цепных подстановок. Его сущность заключается в постепенной и последовательной замене значений факторов на начало отчетного периода их значениями на конец отчетного периода и в выявлении разности между последующим и предыдущим значениями результативного показателя (финансового коэффициента).
При применении приема цепных подстановок следует помнить следующие правила.
1) Если в исследуемой модели есть ярко выраженные экстенсивные и интенсивные факторы, то сначала заменяется значение экстенсивного фактора, а уже затем – интенсивного.
Если в исследуемой модели присутствуют только экстенсивные факторы, среди которых можно выделить наиболее общий и частные, то вначале производится замена значений наиболее общего фактора с последующим переходом к замене частых факторов. Например, общая величина активов (валюта баланса) является более общим показателем, нежели их составляющие (основные средства, запасы и др.).
2) Если влияние фактора уже найдено, в последующих расчетах он берется в фактической оценке отчетного периода, для показателей, исследуемых за период, либо в оценке на конец отчетного периода – для моментных данных. Если влияние фактора еще не найдено, в последующих расчетах его значение берется либо в базисной оценке, либо в оценке на начало отчетного периода соответственно.
3) Число подстановок должно быть на единицу больше, чем факторов, а число скорректированных значений результативного показателя – на единицу меньше.
Проиллюстрируем сущность приема цепных подстановок, используя модель условного финансового коэффициента:
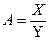 , (11)
, (11)
где А – значение финансового коэффициента (результативного показателя);
Х, Y – абсолютные значения финансовых показателей, выступающих в качестве факторов, причем оба фактора являются экстенсивными, причем Х – более общий экстенсивный фактор, чем Y.
Предварительно на основе горизонтального анализа определим величину абсолютного отклонения его значения за отчетный период:
DА = А К.Г – А Н.Г, (12)
где А К.Г , А Н.Г – значения результативного показателя на начало и конец отчетного периода соответственно.
Методика расчета влияния факторов на изменение результативного показателя в виде финансового коэффициента представлена в таблице 2.
Проиллюстрируем приведенную методику с использованием условных данных:
| Х Н.Г – 100 | Y Н.Г – 200 |
Расчет влияния факторов оформлен в таблице 3.
Таблица 2 - Методика расчета влияния факторов на изменение финансового коэффициента за отчетный год методом цепных подстановок
| Показатели | На начало отчетного года (н.г.) | Скорректированные значения (ск) | На конец отчетного года (к.г.) | Влияние факторов | |
| Расчет | Величина | ||||
| 1. Х | Х Н.Г. | Х К.Г. | Х К.Г. | А СК - А Н.Г. | D А(х) |
| 2. Y | Y Н.Г. | Y Н.Г. | Y К.Г. | А К.Г. - А СК | D А(у) |
| 3. А (стр.1 : стр.2) | А Н.Г. | А СК | А К.Г. | А К.Г. - А Н.Г. | D А |
Таблица 3 - Расчет влияния факторов на изменение финансового коэффициента за отчетный год методом цепных подстановок
| Показатели | На начало отчетного года
| Скорректированные значения
| На конец отчетного года
| Влияние факторов | |
| Расчет | Величина | ||||
| 1. Х | 100 | 120 | 120 | 0,60-0,50 | 0,10 |
| 2. Y | 200 | 200 | 220 | 0,55-0,60 | -0,05 |
| 3. А (стр.1 : стр.2) | 0,50 | 0,60 | 0,55 | 0,55-0,50 | 0,05 |
Данные приведенного расчета показывают, что значение финансового коэффициента А повысилось за отчетный год на 0,05. При этом факторы влияли в разных направлениях: рост фактора Х привел к увеличению финансового коэффициента на 0,1, а рост фактора Y - к уменьшению финансового коэффициента на 0,05. Проверка показала, что совокупное влияние факторов [0,1+(-0,05)] равно абсолютному изменению финансового коэффициента за отчетный год.
При решении задач прямого детерминированного анализа с целью расширения перечня факторов, влияющих на изменение результативного показателя, а значит, и повышения возможностей поиска внутренних резервов улучшения результатов деятельности, используют моделирование детерминированных систем. В частности, при изучении деловой активности при помощи коэффициентов рентабельности прибегают к такому методу моделирования кратных систем, как их «расширение», осуществляемому путем перемножения числителя и знаменателя факторной исходной системы на один и тот же или несколько одинаковых факторов с получением конечной системы в виде мультипликативной модели с новым набором факторов.
В задачах обратного факторного анализа производится агрегирование значений частных показателей в обобщающий (интегральный). Такие задачи решаются в ходе определения уровня финансовой устойчивости, диагностики банкротства.
С целью получения конкретных данных при отборе частных показателей следует учитывать их соответствие двум основным требованиям:
- во-первых, однонаправленности – повышение значения каждого частного показателя должно приводить к повышению уровня комплексного, т. е. к улучшению значения изучаемой стороны финансового состояния;
- во-вторых, соразмерности частных показателей между собой в системе комплексной оценки. С целью удовлетворения этого требования в качестве значений частных показателей в ходе анализа финансового состояния предпочтительнее выбирать частные коэффициенты, варьирующие в пределах от 0 до 1.
Далее необходимо выбрать наиболее приемлемые из существующих методов изучения обратной детерминированной факторной связи.
Учитывая специфику решаемых задач, возможно использование с этой целью методов сумм средней арифметической простой, средней геометрической, коэффициентов.
Название метода определяется математической процедурой, положенной в основу формирования комплексного показателя.
Базовые формулы для расчета комплексного показателя указанными выше методами имеют вид:
1) метод сумм:
К 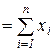 , (13)
, (13)
где К – значение комплексного показателя;
x i – значение i -го частного показателя;
n – число частных показателей;
2) метод средней арифметической:
К 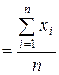 ; (14)
; (14)
3) метод средней геометрической:
К= 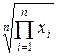 ; (15)
; (15)
4) метод коэффициентов:
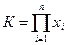 . (16)
. (16)
Апробация предлагаемой методики комплексного показателя на базе частных коэффициентов оформляется в виде таблицы 4.
Таблица 4 - Расчет комплексного финансового показателя различными методами
| Наименование показателей (коэффициентов) | Значения коэффициентов | Абсолютное отклонение (+;-) | |
| на начало периода | на конец периода | ||
| А | 1 | 2 | 3 (2-1) |
| Частный коэффициент – Х1 | 0,63 | 0,65 | 0,02 |
| Частный коэффициент – Х 2 | 0,57 | 0,54 | -0,03 |
| Частный коэффициент – Х 3 | 0,71 | 0,68 | -0,03 |
| Частный коэффициент – Х 4 | 0,38 | 0,45 | 0,07 |
| Комплексный показатель, рассчитанный методом средней арифметической простой (стр.1+стр.2+стр.3+стр.4) / 4 | 0,57 | 0,58 | 0,01 |
Комплексный показатель, рассчитанный методом средней геометрической
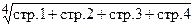
| 0,56 | 0,57 | 0,01 |
| Комплексный показатель, рассчитанный методом коэффициентов (стр.1 * стр.2 * стр.3 * стр.4) | 0,097 | 0,107 | 0,01 |
Расчеты, приведенные в таблице 4, показывают, что при использовании средней арифметической простой и средней геометрической получают практически одинаковые значения комплексного показателя, которые одновременно соизмеримы со значением частных коэффициентов, что и позволяет отдать им предпочтение из возможных методов формирования комплексной оценки.
При этом наиболее простым при наличии нечетного числа частных коэффициентов является метод средней арифметической простой, что и позволяет рекомендовать его к использованию в практических расчетах.
Указанные выше стандартные методы анализа финансового состояния дополняются графическими методами, позволяющими повышать степень наглядности результатов анализа, систематизированных в специальных аналитических таблицах. К наиболее часто встречающимся видам графиков при изучении состава и структуры финансовых ресурсов и имущества относятся круговые диаграммы .
Дата: 2018-11-18, просмотров: 396.