При моделировании системы S методом имитационного моделирования, в частности методом статистического моделирования на ЭВМ, существенное внимание уделяется учету случайных факторов и воздействий на систему. Формирование на ЭВМ реализаций случайных объектов любой природы из перечисленных сводится к генерации и преоб­разованию последовательностей случайных чисел.

Моделирование случайных событий. Пусть имеются случайные числа x_i т. е. возможные значения случайной величины x, равномерно распределенной в интервале (О, 1). Необходимо реализовать случайное событие А, наступающее с заданной вероятностью р. Определим А как событие, состоящее в том, что выбранное значение x_i, случайной величины x удовлет­воряет неравенству 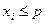 . (1)

Тогда вероятность события А будет 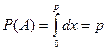 Тогда .

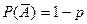Процедура моделирования в этом случае состоит в выборе значений x_i, и сравнении их с р. При этом, если условие (1) выполняется, исходом испытания является событие А.

Таким же образом можно рассмотреть группу событий. Пусть A₁, A₂, …, A_s — полная группа событий, наступающих с вероят­ностями p₁, p₂, …, p_s, соответственно. Определим А _m как событие, состоящее в том, что выбранное значение x_i случайной величины x удовлетворяет неравенству

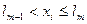,    (2) где 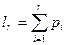. Тогда .    

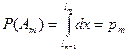Процедура моделирования испытаний в этом случае состоит в последовательном сравнении случайных чисел x_i, со значениями l_r . Исходом испытания оказывается событие А _m, если выполняется условие (2). Эту процедуру называют определением исхода испытания по жребию в соответствии с вероятностями p₁, p₂, …, p_s.

Эти процедуры моделирования были рассмотрены в предполо­жении, что для испытаний применяются случайные числа x_i, имеющие равномерное распределение в интервале (О, 1). При моделировании на ЭВМ используются псевдослучайные числа с квазиравномерным распределением, что приводит к некоторой ошибке.

Моделирование непрерывных случайных величин. Рассмотрим особенности генерации на ЭВМ непрерывных случайных величин. Непрерывная случайная величина h задана интегральной функцией распределения

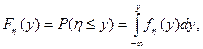
где 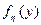— плотность вероятностей.

 можно воспользоваться методом обратной функции. Взаимно однозначна монотонная функция 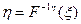, полученная решением относительно h уравнения 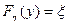, преобразует равномерно распределенную на интервале (О, 1) величину x в h с требуемой плотностью .

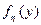Действительно, если случайная величина h имеет плотность рас­пределения 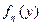, то распределение случайной величины

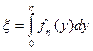
является равномерным в интервале (О, 1). Чтобы получить число, принад­лежащее последовательности случайных чисел {у _j}, имеющих функ­цию плотности f_n (у), необходимо разрешить относительно y_j урав­нение

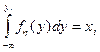. (7)

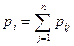Моделирование случайных векторов. Случайный вектор можно задать проекциями на оси координат, причем эти проекции являются случайными величинами, описываемыми совместным законом распределения. Рассмотрим дискретный случайный процесс, когда двухмерная случайная величина (x, h) является дискретной и ее составляющая  принимает возможные значения x₁, x₂, …, x_n, а составляющая h — значения y₁, y₂, …, y_n, причем каждой паре ( x_i, y_j) соответствует вероятность р _ij.   Тогда каждому возможному значению x_i случайной величины x будет соответствовать .

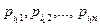Тогда в соответствии с этим распределением вероятностей мож­но определить конкретное значение x_i случайной величины x (по правилам, рассмотренным ранее) и из всех значений p_ij выбрать последовательность

(8) которая описывает условное распределение величины h при усло­вии, что x = x_i. Затем определяем конкретное значение 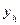 случайной величины h в соответствии с распределением вероятностей. Полученная пара 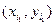будет первой реализацией моделируемого случайного вектора. Далее определяем возможные значения 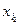, выбираем последова­тельность

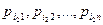                        (9)

и находим 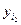 в соответствии с распределением (9). Это дает реализацию вектора  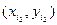и т. д.

Рассмотрим моделирование непрерывного случайного вектора с составляющими x и h. В этом случае двухмерная случайная величина (x, h) описывается совместной функцией плотности f(х, у). Эта функция может быть использована для определения функции плотности случайной величины как

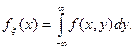
Имея функцию плотности 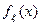, можно найти случайное число х _i, а затем при условии, что x = х _i, определить условное распределение случайной величины h:

В соответствии с этой функцией плотности можно определить случайное число у _i. Тогда пара чисел ( x_i, y_i) будет являться искомой реализацией вектора (x, h).

Рассмотренный способ формирования реализаций двухмерных векторов можно обобщить и на случай многомерных случайных векторов. Однако при больших размерностях этих векторов объем вычислений существенно увеличивается, что создает препятствия к использованию этого способа в практике моделирования систем.

Требования к языкам имитационного моделирования.

В ЯИМ должен быть предусмотрен набор таких программных средств и понятий, которые не встречаются в обычных ЯОН.

Совмещение. Параллельно протекающие в реальных системах S процессы представляются с помощью последовательно работающей ЭВМ. Языки моделирования позволяют обойти эту трудность путем введения понятия системного времени, используемого для представления упорядоченных во времени событий.

Размер. Большинство моделируемых систем имеет сложную структуру . Поэтому используют динамическое распределение памяти, когда компоненты модели системы М_м появляются в оперативной памяти ЭВМ или покидают ее в зависимости от текущего состояния. Важным аспектом реализуемости модели М_м на ЭВМ в этом случае является блочность

Изменения. во всех ЯИМ предусматривают обработку списков, отражающих изменения состояний процесса функционирования моделируемой системы S.

Взаимосвязанность. Условия, необходимые для свершения различных событий в модели М_м процесса функционирования системы S, могут оказаться весьма сложными. Для разрешения связанных с этим вопросом трудностей в большинство ЯИМ включают соответствующие логические возможности и понятия теории множеств.

Стохастичность. Для моделирования случайных событий и про­цессов используют специальные программы генерации последовате­льностей псевдослучайных чисел, квазиравномерно распределенных на заданном интервале, на основе которых можно получить стоха­стические воздействия на модель М_м, имитируемые случайными величинами с соответствующим законом распределения.

Анализ. необходимо получать статистические характеристики процесса функционирования модели системы М( S). Перечисленным требованиям при исследовании и проектирова­нии различных систем S отвечают такие наиболее известные языки моделирования дискретных событий, как SIMULA, SIMSCRIPT, GPSS, SOL, CSL и др.

Основы классификации языков моделирования. Как уже отмеча­лось, для машинного моделирования системы S пригодны три способа проведения вычислений, в основе которых лежит применение цифровой, аналоговой и гибридной вычислительной техники. Классификация языков для программирова­ния моделей систем имеет вид, приведенный на рис. 5.3.

В основе рассматриваемой классификации в некоторых ЯИМ лежит принцип формирования системного времени., но также для синхронизации раз­личных событий и операций в модели системы S, то при отнесении того или иного конкретного языка моделирования к определенному типу нельзя не считаться с типом механизма «системных часов».

Непрерывное представление системы S сводится к составлению уравнений, с помощью которых устанавливается связь между эндогенными и экзогенными переменными модели. Примером такого непрерывного подхода является использование дифференциальных уравнений. Причем в дальнейшем дифференциальные уравнения могут быть применены для непосредственного получения характеристик системы, это, например, реализовано в языке MIMIC. А в том случае, когда экзогенные переменные модели принимают Дискретные значения, уравнения являются разностными. Такой под-код реализован, например, в языке DYNAMO.

Представление системы S в виде типовой схемы, в которой участвуют как непрерывные, так и дискретные величины, называет­ся комбинированным. GASP, включает в себя набор программ, с помощью которых моделируемая система S представляется в виде. Состояние модели системы M( S) описывается набором переменных, некоторые из которых меняются во времени непрерывно. Законы изменения непрерывных компонент заложены в структуру, объединяющую дифференциальные уравнения и условия от­носительно переменных. Предполагается, что в системе могут наступать события двух типов: 1) события, зависящие от состояния z_j; 2) события, зависящие от времени t_i. События первого типа наступа­ют в результате выполнения условий, относящихся к законам изменения непрерывных переменных. Для событий второго типа процесс моделирования состоит в продвижении системного времени от момента наступления события до следующего аналогичного момента. События приводят к изменениям состояния модели системы и зако­нов изменения непрерывных компонент. При использовании языка GASP на пользователя возлагается работа по составлению на языке FORTRAN подпрограмм.