Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

ОСНОВНЫЕ ПОНЯТИЯ МОДЕЛИРОВАНИЯ СИСТЕМ

 

В настоящее время в моделировании и синтезе больших систем сложилось два подхода:

1. системный подход;

2. классический подход.

Системный подход предполагает последовательный переход от общего к частному, когда в основе рассмотрения лежит ЦЕЛЬ, причем исследуемый объект выделяется из окружающей среды.

Структура системы – совокупности связей между элементами системы, отражающих их взаимодействие. Чаще всего структурные связи имеют топологический характер. Системный подход означает, что каждая система S является интегрированным целым даже тогда, когда она состоит из отдельных разобщенных подсистем.

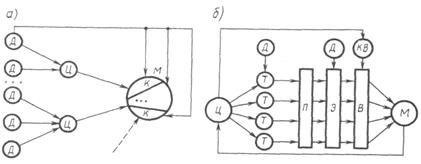
Рис. 2. Процесс синтеза модели на основе классического (а) я системного (б) подходов.

 

Процесс синтеза моделей М на базе системного подхода состоит в следующем: на основе исходных данных Д, известных из анализа внешней среды (системы), технических ограничений, которые накладываются на систему сверху (верхний иерархический уровень), либо исходя из возможности ее реализаций, и на основе цели функционирования используются/формулируются исходные требования Т к модели системы S. На базе этих требований формируются ориентировочно некоторые подсистемы П, элементы Э и осуществляется наиболее сложный этап синтеза – выбор В составляющих системы, используя специальный критерий выбора КВ.

Индуктивный (классический) подход рассматривает систему через переход от частного к общему и синтезирует/конструирует слияния ее компонент, разрабатываемых отдельно.

Реальный объект, подлежащий моделированию, разбивается на отдель­ные подсистемы, т. е. выбираются исходные данные Д для моделирования и ставятся цели Ц, отображающие отдельные сто­роны процесса моделирования. По отдельной совокупности исход­ных данных Д ставится цель моделирования отдельной стороны функционирования системы, на базе этой цели формируется некото­рая компонента К будущей модели. Совокупность компонент объ­единяется в модель М.

Таким образом, разработка модели М на базе классического подхода означает суммирование отдельных компонент в единую модель, причем каждая из компонент решает свои собственные задачи и изолирована от других частей модели. Поэтому классический подход может быть использован для реализации сравнительно простых моделей, в которых возможно разделение и взаимно неза­висимое рассмотрение отдельных сторон функционирования реаль­ного объекта. Для модели сложного объекта такая разобщенность решаемых задач недопустима, так как приводит к значительным затратам ресурсов при реализации модели на базе конкретных программно-технических средств. Можно отметить две отличитель­ные стороны классического подхода: наблюдается движение от частного к общему, создаваемая модель (система) образуется путем суммирования отдельных ее компонент и не учитывается возник­новение нового системного эффекта.

Моделирование – это зачастую поиск обобщений. Существуют два вида обобщений:

1. дешевый;

2. ценный.

Легко обобщать путем разряжения, важно обобщить путем сгущения.

На базе системного подхода предполагаются две основные стадии проектирования:

1. Макропроектирование – на основе данных о внешней среде Е и о реальной системе S строится модель внешней среды, выявляются ресурсы и ограничения для построения моделей системы; выбираются модели системы и критерии, позволяющие оценить адекватность модели М реальной системы S.

2. Микропроектирование – более зависит от конкретного типа выбранной модели. В случае имитационного моделирования необходимо обеспечить создание информационного, математического, технического и программного обеспечения. На этой стадии можно установить основные характеристики созданной модели, оценить время работы с ней и затраты ресурсов.

 

ФОРМАЛЬНАЯ МОДЕЛЬ ОБЪЕКТА

Некоторое напоминание о математических понятиях:

Модель объекта моделирования, т. е. системы S, можно представить в виде множества величин, описывающих процесс функционирования реальной системы и об­разующих в общем случае следующие подмножества:

совокупность входных воздействий на систему

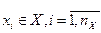, где n – число входных воздействий;

совокупность воздействий внешней среды

;

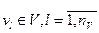совокупность внутренних (собственных) параметров системы

,

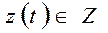которые являются независимыми (экзогенными) переменными и в векторной форме имеют вид:

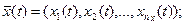
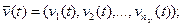
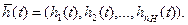
И совокупность выходных характеристик системы

,

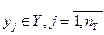которые являются зависимыми (эндогенными) переменными:

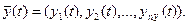
Процесс функционирования системы S описывается во времени оператором F_s, который в общем случае преобразует экзогенные переменные в эндогенные в соответствии с соотношениями вида

,

y( t)= F_s( x, v, h, t).

Совокупность зависимостей выходных характеристик системы от времени 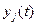для всех видов 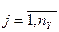, и_г называется выходной траек­торией 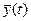. Зависимость (1) называется законом функционирова­ния системы S и обозначается F_s. В общем случае закон функци­онирования системы F_s может быть задан в виде функции, функци­онала, логических условий, в алгоритмической и табличной формах или в виде словесного правила соответствия.

алгоритма функционирования A_s, под которым понимается метод получения выходных характеристик с учетом входных воздействий 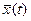, воздействий внешней среды  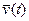и собственных параметров системы 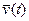. Динамические модели – это математические модели, описывающие поведение объекта системы во времени, т.е. отображающие его динамические свойства.

Для статических моделей математическая модель представляет собой отображение между двумя подмножествами свойств моделируемого объекта Y и { X, V, Н], что в векторной форме может быть записано как

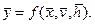
Соотношения параметров модели, выраженные в определенные моменты времени, называют состояниями (срезами). Состояние системы S характеризуется векторами:

;

,

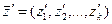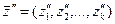где , ,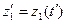

, ,

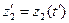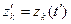
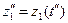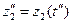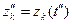
в момент , .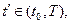

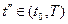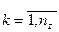Если рассматривать процесс функционирования системы S как последовательную смену состояний z₁( t), z₂( t), ..., z_k( t), то они могут быть интерпретированы как координаты точки в k-мерном фазовом пространстве, причем каждой реализации процесса буде соответствовать некоторая фазовая траектория. Совокупность все возможных значений состояний { z} называется пространством состояний объекта моделирования Z, причем z_k Î Z.

Состояния системы S в момент времени 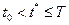 полностью определяются начальными условиями 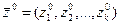, где 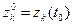; входными воздействиями 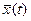; внутренними параметрами 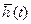и воздействиями внешней сре­ды 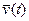, которые имели место за промежуток времени ( t^* - t₀) с помощью двух векторных уравнени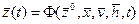й:

 и ,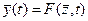

т.е. 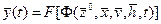 (вход® состояние® выход).

Язык моделирования отличается от языка математики тем, что в языке математики состояние системы никого не интересует, т.е. вход® выход. В моделировании вход® состояние® выход, главное состояние.

В общем случае время в модели системы S может рассматриваться на интервале моделирования (0, T) как непрерывное, так и дискретное, т. е. квантованное на отрезки длиной D t временных единиц каждый, когда T= m D t, где 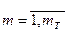— число интервалов дискретизации.

Таким образом, под математической моделью объекта (реаль­ной системы) понимают конечное подмножество переменных 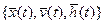вместе с математическими связями между ними и харак­теристиками .

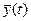Если математическое описание объекта моделирования не содержит элементов случайности или они не учитываются, то модель называется детерминированной в том смысле, что характеристики однозначно определяются детерминированными входными воздействиями

Если учитываются стохастические воздействия внешней среды 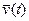 и стохастические внутренние параметры 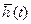, то это стохастическая модель.

 

Виды моделирования

ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ

При случае использования имитационных моделей в отличие от аналитических в ЭВМ воспроизводится текущее функционирование технической системы в некотором, удобном для пользователей, масштабе времени.

Входные воздействия воспроизводятся в виде наборов чисел – реализации процессов (а не числовых характеристик как при аналитическом моделировании).

Могут воспроизводиться также промежуточные преобразования обрабатываемого сигнала. В динамическом режиме работы имитационной модели может меняться корреляционная функция работы входных чисел с последующим отображением корреляции функции выходного сигнала.

Имитационное моделирование напоминает физический эксперимент (наглядность результатов моделирования, в том числе и промежуточных).

Достоинства имитационного моделирования:

1. возможность моделирования даже тогда, когда аналитические модели либо отсутствуют, либо (из-за сложности системы) не дают достоверных результатов (например перевод на разные языки, распознавание образов);

3. простота выработки управляющих воздействий на модель;

4. позволяет учесть влияние большого числа случайных и детерминированных факторов, а так же сложных зависимостей при вводе в модель соответствующих элементов и операций;

5. с точки зрения сбора статистических данных дает возможность проводить активный эксперимент с помощью целенаправленных изменений параметров модели на некотором множестве реализации, что позволяет оптимизировать модель.

При решении ряда задач могут применяться имитационные модели, отображающие только структурные, топологические (геометрические) свойства объектов. Такие структурные модели могут иметь форму:

1. матриц;

2. графов;

3. списка векторов

и выражать возможное расположение элементов в пространстве и их связи (провода, трубопроводы). Структурные модели используют в случаях, когда не учитываются физические процессы в объектах.

ФУНКЦИОНАЛЬНЫЕ МОДЕЛИ

При моделировании сложных технологических объектов возрастает объем входной информации (описание связей, задание параметров элементов модели, и т.д.). Укрупненность элементов модели приводит к возрастанию необходимой номенклатуры элементарных моделей, к увеличению объема моделирующей программы.

Компромисс - разбиение модели на функциональные блоки.

Функциональные модели отражают как структуру так и процессы функционирования объектов, и чаще всего имеют форму систем уравнений.

По способу получения функциональные модели делятся на:

- теоретические;

- формальные.

Формальные функциональные модели получают на основе проявления свойств моделируемого объекта во внешней среде. Они более точны в окрестности той точки пространства параметров, вблизи которой они определялись, но менее точны вдали от нее.

Глубина моделирования.

Моделируя сложные системы используют совокупность из нескольких моделей из числа всех разновидностей.

Любая система или подсистема может быть представлена различными способами, часто взаимодополняющими. В зависимости от глубины анализа простые модели заменяют все более сложные.

СЕТЕВЫЕ МОДЕЛИ ( N-СХЕМЫ)

В практике моделирования объектов часто приходится решать задачи, связанные с формализованным описанием и анализом при­чинно-следственных связей в сложных системах, где одновременно параллельно протекает несколько процессов. Самым распростра­ненным в настоящее время формализмом, описывающим структуру и взаимодействие параллельных систем и процессов, являются сети Петри (англ. Petri Nets), предложенные К. Петри.

Основные соотношения. Теория сетей Петри развивается в нескольких направлениях: разработка математических основ, структурная теория сетей, различные приложения (параллельное програм­мирование, дискретные динамические системы и т. д.).

Формально сеть Петри ( N-схема) задается четверкой вида

N = < B, D, I, O>,

где В — конечное множество символов, называемых позициями, В ¹ Æ; D — конечное множество символов, называемых перехода­ми, D ¹ Æ, B Ç D ¹ Æ; I — входная функция (прямая функция ин­цидентности), I: B x D ® {0, 1}; О — выходная функция (обратная функция инцидентности), О : D х В ® {0,1}.

 

Требования к языкам имитационного моделирования.

В ЯИМ должен быть предусмотрен набор таких программных средств и понятий, которые не встречаются в обычных ЯОН.

Совмещение. Параллельно протекающие в реальных системах S процессы представляются с помощью последовательно работающей ЭВМ. Языки моделирования позволяют обойти эту трудность путем введения понятия системного времени, используемого для представления упорядоченных во времени событий.

Размер. Большинство моделируемых систем имеет сложную структуру . Поэтому используют динамическое распределение памяти, когда компоненты модели системы М_м появляются в оперативной памяти ЭВМ или покидают ее в зависимости от текущего состояния. Важным аспектом реализуемости модели М_м на ЭВМ в этом случае является блочность

Изменения. во всех ЯИМ предусматривают обработку списков, отражающих изменения состояний процесса функционирования моделируемой системы S.

Взаимосвязанность. Условия, необходимые для свершения различных событий в модели М_м процесса функционирования системы S, могут оказаться весьма сложными. Для разрешения связанных с этим вопросом трудностей в большинство ЯИМ включают соответствующие логические возможности и понятия теории множеств.

Стохастичность. Для моделирования случайных событий и про­цессов используют специальные программы генерации последовате­льностей псевдослучайных чисел, квазиравномерно распределенных на заданном интервале, на основе которых можно получить стоха­стические воздействия на модель М_м, имитируемые случайными величинами с соответствующим законом распределения.

Анализ. необходимо получать статистические характеристики процесса функционирования модели системы М( S). Перечисленным требованиям при исследовании и проектирова­нии различных систем S отвечают такие наиболее известные языки моделирования дискретных событий, как SIMULA, SIMSCRIPT, GPSS, SOL, CSL и др.

Основы классификации языков моделирования. Как уже отмеча­лось, для машинного моделирования системы S пригодны три способа проведения вычислений, в основе которых лежит применение цифровой, аналоговой и гибридной вычислительной техники. Классификация языков для программирова­ния моделей систем имеет вид, приведенный на рис. 5.3.

В основе рассматриваемой классификации в некоторых ЯИМ лежит принцип формирования системного времени., но также для синхронизации раз­личных событий и операций в модели системы S, то при отнесении того или иного конкретного языка моделирования к определенному типу нельзя не считаться с типом механизма «системных часов».

Непрерывное представление системы S сводится к составлению уравнений, с помощью которых устанавливается связь между эндогенными и экзогенными переменными модели. Примером такого непрерывного подхода является использование дифференциальных уравнений. Причем в дальнейшем дифференциальные уравнения могут быть применены для непосредственного получения характеристик системы, это, например, реализовано в языке MIMIC. А в том случае, когда экзогенные переменные модели принимают Дискретные значения, уравнения являются разностными. Такой под-код реализован, например, в языке DYNAMO.

Представление системы S в виде типовой схемы, в которой участвуют как непрерывные, так и дискретные величины, называет­ся комбинированным. GASP, включает в себя набор программ, с помощью которых моделируемая система S представляется в виде. Состояние модели системы M( S) описывается набором переменных, некоторые из которых меняются во времени непрерывно. Законы изменения непрерывных компонент заложены в структуру, объединяющую дифференциальные уравнения и условия от­носительно переменных. Предполагается, что в системе могут наступать события двух типов: 1) события, зависящие от состояния z_j; 2) события, зависящие от времени t_i. События первого типа наступа­ют в результате выполнения условий, относящихся к законам изменения непрерывных переменных. Для событий второго типа процесс моделирования состоит в продвижении системного времени от момента наступления события до следующего аналогичного момента. События приводят к изменениям состояния модели системы и зако­нов изменения непрерывных компонент. При использовании языка GASP на пользователя возлагается работа по составлению на языке FORTRAN подпрограмм.

ПРОГРАММНЫЕ СРЕДСТВА АСМ

(АВТОМАТИЗИРОВАННЫЕ СИСТЕМЫ МОДЕЛИРОВАНИЯ)

 

Формирование БД объекта моделирования (БДО) и БД о машинном эксперименте (БДЭ). Под ППМ, ориентированным на решение задач машинного моделирования систем, понимается комплекс программных средств и документов, предназначенных для реализации алгоритма процесса функционирования системы S и обеспечивающих автоматизацию управления ведением эксперимента с моделью М_м на ЭВМ.

Сущность такого определения состоит в том, что ППМ представляет набор средств для разработки программ моделирования, служащих для автоматизации определенных функций. К программным средствам ППМ относится набор про­граммных модулей (тело пакета), из которых набирается программа. В состав ППМ также входят управляющая программа, представляющая собой аналог супервизора ЭВМ (средства генерации рабочих программ). Специальная программа (монитор) принимает от пользователя информацию о требуемой модификации программ, формирует из набора стандартных модулей законченные рабочие программы, гибкость .

Различают две разновидности моделирования: статическую-нельзя изменять готовую программу и динамическую-можно изменять готовую программу путем использования таблицы сносок подпрограмм задействованных в данной программе, требует больших затрат ресурсов..озможность замены имеющихся модулей ППМ на собственные.

Таким образом, программные средства ППМ объединяют в себе три главных качества: 1) содержат алгоритмические решения по проведению моделирования, доведенные до законченной машинной реализации; 2) имеют механизм автоматической настройки; 3) позволяют дополнять генерируемые ППМ рабочие программы.

Существенный момент выбор технических средств. Структурно АСМ можно разбить на следующие комплексы программ: формирования базы данных об объекте моделирования (БДО); формирования базы данных о машинном эксперименте (БДЭ); моделирования процесса функционирования объекта; расширения возможностей ППМ; организации различных режимов работы ППМ.

Комплекс программ формирования БДО реализует все работы по созданию в АСМ сведений о моделируемом объекте. Информация об объекте может корректироваться по мере получения новых сведений в процессе машинного модели­рования. Для формирования БДО требуются следующие программы: ввода данных об объекте; перевода в стандартную форму; диспетчеризации процедур ввода; формирования БДО.

Для решения задачи моделирования требуются следующие программы: управления машинным экспериментом, реализации и его диспетчеризация; машинной имитации, Имеются программные пакеты GSPT, Vissim, SIMEX, GPSS/ H, Stella, SimPack, DOBSim, Mosis, QSIM, SIMPLORER, Modsim и де­сятки других. Языки данного класса хорошо согласуются с удобным опи­санием модели системы в форме Q-схемы (системы массового об­служивания).

26. Особенности языка моделирования GPSS.

дискретных систем GPSS.. достоинство— наличие необходимого набора типовых элементов и программная реализация алгоритмов, позволяющая строить сложные модели.

В пакете GPSS используется язык блок-диаграмм. Блок-диаграммой в пакете GPSS называется графическое представление операций, происходящих в моделируемой системе S. В этом случае блок-диаграмма описывает взаимодействия, происходящие внутри моделируемой системы S в процессе ее функционирования.

Рис. 12. Схема процесса создания машинной модели с ис­пользованием языка GPSS

В блок-диаграммах GPSS блоки представляют собой выполняемые над динами­ческими объектами операции, а стрелки между блоками отражают маршруты перед­вижения данных объектов по системе. Альтернативные ситуации отражаются более чем одной стрелкой, выходящей из блока. Процесс разбиения на элемент системы.

Набор операторов языка однозначно соответствует набору блоков для описания блок-диаграмм.Создание ППМ является крупным достижением в автоматизации моделирования больших систем. Однако любой ППМ, создан­ный на базе ЯИМ, характеризуется узостью представлений, диктуемой особенностями. Наиболее эффективно использование ППМ при исследовании и разработке систем на основе метода машинного моделирования при реализации диалоговых процедур и концепции базы данных моделирования.

 

БАЗЫ ДАННЫХ МОДЕЛИРОВАНИЯ

 

Перспективным направлением является использование для целей моделирования иерархических многомашинных информационно-вычислительных систем и связан­ных с ними телекоммуникационными сетями удаленных персональ­ных ЭВМ, работающих в режиме телеобработки. Таким образом, появляется необходимость в создании диалоговых систем моделирования коллективного пользования. Рассмотрим основные моменты связанные с разработкой распределенной базы данных моделирования (РБДМ).

Ключевые аспекты разработки баз данных. Важной целью применения технологии БД является создание разделяемого между функционально связанными приложениями информационного ресурса с обеспечением независимости внешнего, логического представления БД от способов ее внутренней, физической организации. в основу этой технологии положено применение реляционной модели данных (РМД), базирующейся на аппарате реляционной алгебры и математической логики. на рис. 13.

База данных. Определение базы данных в качестве разделяемого инфор­мационного ресурса компьютеризированных технологий база данных совокупность связанных данных, с одной стороны, являющихся информацией, и с другой стороны, составляющих основу для получения информации,

 

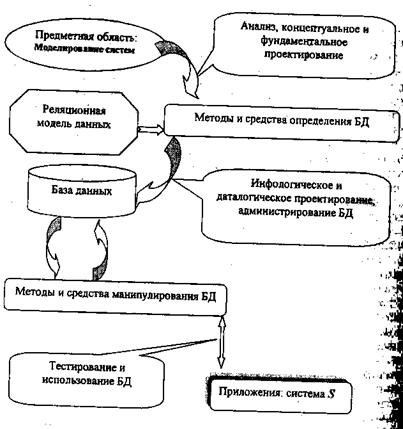
Рис. 13. Полная технологическая схема реализация БДМ

 

Предметная область. предметная область, которая будет рассматри­ваться как совокупность знаний и данных об объектах и процессах, подлежащих проектированию и хранению в БД.

Таким образом, процесс проектирования базы данных по полной технологической схеме есть процесс пошагового отображения исходной классификационной схемы предметной области в реляционную схему реализации базы данных.

Инфологический анализ и проектирование БДМ. Для инфологического проектирования характерны следующие операции:

— расширение интерфейсов описания абстракций не классифицированными свойствами

— построение инфологических структур реализации модели, в качестве структур могут использоваться любые структуры

Инфологическая модель, является основой определения источников, накопителей и получателей информации. Совокупность правил построения инфологической модели об­разует инфологическую семантику проектируемой БД, состоящую из определений связей совместности и соответствия. Она определяет пути доступа к информации . концептуальные компоненты являются символами, а инфологически компоненты соответствуют логическим словам и выражениям.

Объектно-ориентированный подход и БДМ. связан с представлени­ем предметной области в виде классов и объектов, которые в зависимости от предназначения методологии могут иметь различную природу.. Возможность применения ОП определяется способностью представить предмет моделирования в виде объектной модели.Visual C++, C++ Builder, Delphi.

ОП применяется при разработке объектно-ориентированных баз данных (ООБД) и объектно-ориентированных распределенных баз данных (ООРБД). Центральной проблемой является оптимальное сочетание объектно-ориентированного и реляционного подходов (см. рис. 5.6).

ПЛАНИРОВАНИЕ ИМИТАЦИОННЫХ ЭКСПЕРИМЕНТОВ

Основные понятия планирования экспериментов. наиболее подходящей моделью последнего является абстрактная схема, называемая «черным ящиком». При таком кибернетичес­ком подходе различают входные и выходные переменные: x₁, x₂,…, x_k; y₁, y₂, …, y_i. В зависимости от того, какую роль играет каждая переменная в проводимом эксперименте, она может являться либо фактором, либо реакцией.. Например, в агрегативной системе (А-схеме) факторами будут входные и управля­ющие сообщения, а реакциями — выходные.

Каждый фактор х _i, 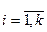, может принимать в эксперименте одно из нескольких значений, называемых уровнями. Фиксированный набор уровней факторов определяет одно из возможных состояний рассматриваемой системы. Одновременно этот набор пред­ставляет собой условия проведения одного из возможных экспериментов.

Каждому фиксированному набору уровней факторов соответствует определенная точка в многомерном пространстве, называемом факторным пространством., это показано для случая двух факторов х₁ и х₂ на рис. 14 (плоскость х₁0₁х₂).

Существует вполне определенная связь между уровнями факторов и реакцией системы, которую можно представить в виде соотношения

.

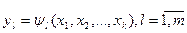Функцию 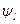, связывающую реакцию с факторами, называют функцией реакции, а геометрический образ, соответствующий функции реакции,— поверхностью реакции. Исследователю заранее не известен вид зависимостей 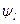, , 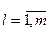поэтому используют приближенные соотношения:

.

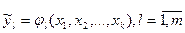Зависимости 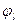 находятся по данным эксперимента. Последний необходимо поставить при минимальных ресурсов (построить математическую модель системы и оценить ее характеристики. Факторы при проведении экспериментов могут быть управляемыми и неуправляемыми, наблюдаемыми и ненаблюдаемыми, изучаемыми и неизучаемыми, количественными и качественными, фиксированными и случайными.

Фактор называется управляемым, если его уровни целенаправленно выбираются исследователем в процессе эксперимента. Фактор называется наблюдаемым, если его значения наблюдаются и регистрируются. Обычно в машинном эксперименте с моделью М_м наблюдаемые факторы совпадают с управляемыми, так как нерационально управлять фактором, не наблюдая его. Но неуправляемый фактор также можно наблюдать. Наблюдаемые неуправляемые факторы. Обычно при машинном эксперименте с мо­делью М_м число сопутствующих факторов велико, поэтому рационально учитывать влияние лишь тех из них, которые наиболее существенно воздействуют на интересующую исследователя реак­цию.

Фактор относится к изучаемым, если он включен в модель М_м для изучения свойств системы S, а не для вспомогательных целей, например для увеличения точности эксперимента.

Фактор будет количественным, если его значения — числовые величины, влияющие на реакцию, а в противном случае фактор называется качественным. Фактор называется фиксированным, если в эксперименте иссле­дуются все интересующие экспериментатора значения фактора, а если экспериментатор исследует только некоторую случайную выборку из совокупности интересующих значений факторов, то фактор называется случайным. На основании случайных факторов могут быть сделаны вероятностные выводы и о тех значениях факторов, которые в эксперименте не исследовались.

В машинных экспериментах с моделями М_м не бывает неуправляемых или ненаблюдаемых факторов применительно к исследуемой системе S. В качестве воздействий внешней среды Е, т. е. неуправляемых и ненаблюдаемых факторов, в машинной имитационной модели выступают стохастические экзогенные переменные. Для полного определения фактора необходимо указать последовательность операций, с помощью которых устанавливаются его конкретные уровни. Такое определение фактора называется операциональным и обеспечивает однозначность понимания фактора.

Основными требованиями, предъявляемыми к факторам, являются требование управляемости фактора и требование непосредственного воздействия на объект. При планировании эксперимента обычно одновременно изменяются несколько факторов. Определим требования, которые предъявляются к совокупности факторов. — совмести­мость и независимость. При проведении машинного эксперимента с моделью М_м для оценки некоторых характеристик процесса функционирования ис­следуемой системы S экспериментатор стремится создать такие условия, которые способствуют выявлению влияния факторов, находящихся в функциональной связи с искомой характеристикой.

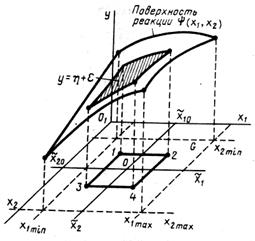Для этого необходимо: отобрать факторы х _i, 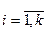, влияющие на искомую характеристику, и описать функциональную зависимость; установить диапазон изменения факторов 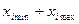; определить координаты точек факторного пространст­ва {x_l, x₂, ..., x_k}, в которых следует проводить экспери­мент; оценить необходимое число реализаций и их поря­док в эксперименте.

 

Для выбора конкретной модели необходимо сформулировать такие особенности, как адекватность, содержательность, простота. Под содержательностью модели планирования понимается ее способность объяснять множество уже известных фактов, выявлять новые и предсказывать их дальнейшее развитие. Простота — одно из главных достоинств модели планирования, выражающееся в реализуемости эксперимента на ЭВМ.

Виды планов экспериментов. Эксперимент, в котором реализуют­ся все возможные сочетания уровней факторов, называется полным факторным экспериментом (ПФЭ). Если выбранная модель планирования включает в себя только линейные члены полинома и их произведения, то для оценки коэффициентов модели используется план эксперимента с варьированием всех k факторов на двух уров­нях, т. е. q=2. Такие планы называются планами типа 2^k, где N=2 ^k — число всех возможных испытаний.

Начальный этап планирования эксперимента для получения коэффициентов линейной модели основан на варьировании факторов на двух уровнях: нижнем х _iн и верхнем x_iв— симметрично рас­положенных относительно основного уровня х _i0, 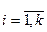. Геометрическая интерпретация показана на рис. 15, а. Так как каждый фактор принимает лишь два значения x_iн = x_i0 - D x, и x_iв = x_i0 + D x, то для стандартизации и упрощения записи условий каждого ис­пытания и обработки выборочных данных эксперимента масштабы по осям факторов выбираются так, чтобы нижний уровень соответ­ствовал — 1, верхний— +1, а основной — нулю. Это легко достигается с помощью преобразования вида

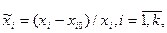
где 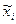   — кодированное значение i-го фактора; х _i — натуральное зна­чение фактора; x_i0 — нулевой уровень; 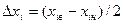— интервал варьирования фактора.

Расположение точек для ПФЭ типа 2² показано на рис. 14, а также на рис. 15, б. Выписывая комбинации уровней факторов для каждой экспериментальной точки квадрата, получим план D полно­го факторного эксперимента типа 2²:

 

Номер испытания	1	2	3	4
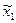
	-1	+1	-1	+1
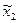
	-1	-1	+1	+1
Обозначения строк	(1)	a	b	ab

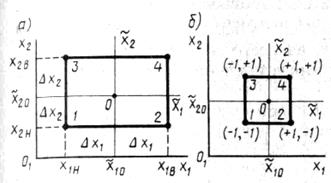
При этом планы можно записывать сокращенно с помощью условных буквенных обозначений строк. Для этого порядковый номер фактора ставится в соответствие строчной букве латинского алфавита: x₁ ®- a, x₂ ® b и т. д.

Затем для каждой строки плана выписываются латинские буквы только для факторов, находящихся на верхних уровнях; испытание со всеми факторами на нижних уровнях обозначается как (1). Запись плана в буквенных обозначениях показана в последней строчке.

Рис. 15. Геометрическая интерпретация полного факторного эксперимента типа 2²: а — без масштабирования; 6 — при масштабировании по осям.

 

 

ОСНОВНЫЕ ПОНЯТИЯ МОДЕЛИРОВАНИЯ СИСТЕМ

 

В настоящее время в моделировании и синтезе больших систем сложилось два подхода:

1. системный подход;

2. классический подход.

Системный подход предполагает последовательный переход от общего к частному, когда в основе рассмотрения лежит ЦЕЛЬ, причем исследуемый объект выделяется из окружающей среды.

Структура системы – совокупности связей между элементами системы, отражающих их взаимодействие. Чаще всего структурные связи имеют топологический характер. Системный подход означает, что каждая система S является интегрированным целым даже тогда, когда она состоит из отдельных разобщенных подсистем.

Рис. 2. Процесс синтеза модели на основе классического (а) я системного (б) подходов.

 

Процесс синтеза моделей М на базе системного подхода состоит в следующем: на основе исходных данных Д, известных из анализа внешней среды (системы), технических ограничений, которые накладываются на систему сверху (верхний иерархический уровень), либо исходя из возможности ее реализаций, и на основе цели функционирования используются/формулируются исходные требования Т к модели системы S. На базе этих требований формируются ориентировочно некоторые подсистемы П, элементы Э и осуществляется наиболее сложный этап синтеза – выбор В составляющих системы, используя специальный критерий выбора КВ.

Индуктивный (классический) подход рассматривает систему через переход от частного к общему и синтезирует/конструирует слияния ее компонент, разрабатываемых отдельно.

Реальный объект, подлежащий моделированию, разбивается на отдель­ные подсистемы, т. е. выбираются исходные данные Д для моделирования и ставятся цели Ц, отображающие отдельные сто­роны процесса моделирования. По отдельной совокупности исход­ных данных Д ставится цель моделирования отдельной стороны функционирования системы, на базе этой цели формируется некото­рая компонента К будущей модели. Совокупность компонент объ­единяется в модель М.

Таким образом, разработка модели М на базе классического подхода означает суммирование отдельных компонент в единую модель, причем каждая из компонент решает свои собственные задачи и изолирована от других частей модели. Поэтому классический подход может быть использован для реализации сравнительно простых моделей, в которых возможно разделение и взаимно неза­висимое рассмотрение отдельных сторон функционирования реаль­ного объекта. Для модели сложного объекта такая разобщенность решаемых задач недопустима, так как приводит к значительным затратам ресурсов при реализации модели на базе конкретных программно-технических средств. Можно отметить две отличитель­ные стороны классического подхода: наблюдается движение от частного к общему, создаваемая модель (система) образуется путем суммирования отдельных ее компонент и не учитывается возник­новение нового системного эффекта.

Моделирование – это зачастую поиск обобщений. Существуют два вида обобщений:

1. дешевый;

2. ценный.

Легко обобщать путем разряжения, важно обобщить путем сгущения.

На базе системного подхода предполагаются две основные стадии проектирования:

1. Макропроектирование – на основе данных о внешней среде Е и о реальной системе S строится модель внешней среды, выявляются ресурсы и ограничения для построения моделей системы; выбираются модели системы и критерии, позволяющие оценить адекватность модели М реальной системы S.

2. Микропроектирование – более зависит от конкретного типа выбранной модели. В случае имитационного моделирования необходимо обеспечить создание информационного, математического, технического и программного обеспечения. На этой стадии можно установить основные характеристики созданной модели, оценить время работы с ней и затраты ресурсов.

 

ФОРМАЛЬНАЯ МОДЕЛЬ ОБЪЕКТА

Некоторое напоминание о математических понятиях:

Модель объекта моделирования, т. е. системы S, можно представить в виде множества величин, описывающих процесс функционирования реальной системы и об­разующих в общем случае следующие подмножества:

совокупность входных воздействий на систему

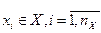, где n – число входных воздействий;

совокупность воздействий внешней среды

;

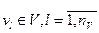совокупность внутренних (собственных) параметров системы

,

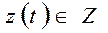которые являются независимыми (экзогенными) переменными и в векторной форме имеют вид:

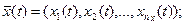
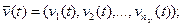
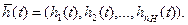
И совокупность выходных характеристик системы

,

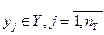которые являются зависимыми (эндогенными) переменными:

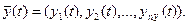
Процесс функционирования системы S описывается во времени оператором F_s, который в общем случае преобразует экзогенные переменные в эндогенные в соответствии с соотношениями вида

,

y( t)= F_s( x, v, h, t).

Совокупность зависимостей выходных характеристик системы от времени 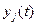для всех видов 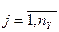, и_г называется выходной траек­торией 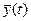. Зависимость (1) называется законом функционирова­ния системы S и обозначается F_s. В общем случае закон функци­онирования системы F_s может быть задан в виде функции, функци­онала, логических условий, в алгоритмической и табличной формах или в виде словесного правила соответствия.

алгоритма функционирования A_s, под которым понимается метод получения выходных характеристик с учетом входных воздействий 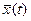, воздействий внешней среды  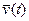и собственных параметров системы 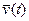. Динамические модели – это математические модели, описывающие поведение объекта системы во времени, т.е. отображающие его динамические свойства.

Для статических моделей математическая модель представляет собой отображение между двумя подмножествами свойств моделируемого объекта Y и { X, V, Н], что в векторной форме может быть записано как

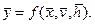
Соотношения параметров модели, выраженные в определенные моменты времени, называют состояниями (срезами). Состояние системы S характеризуется векторами:

;

,

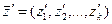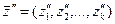где , ,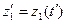

, ,

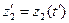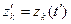
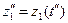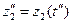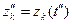
в момент , .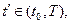

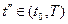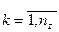Если рассматривать процесс функционирования системы S как последовательную смену состояний z₁( t), z₂( t), ..., z_k( t), то они могут быть интерпретированы как координаты точки в k-мерном фазовом пространстве, причем каждой реализации процесса буде соответствовать некоторая фазовая траектория. Совокупность все возможных значений состояний { z} называется пространством состояний объекта моделирования Z, причем z_k Î Z.

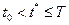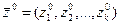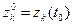Состояния системы S в момент времени  полностью определяются начальными условиями , где ; входными воздействиями 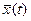; внутренними параметрами 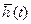и воздействиями внешней сре­ды 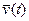, которые имели место за промежуток времени ( t^* - t₀) с помощью двух векторных уравнени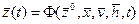й:

 и ,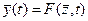

т.е. 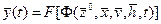 (вход® состояние® выход).

Язык моделирования отличается от языка математики тем, что в языке математики состояние системы никого не интересует, т.е. вход® выход. В моделировании вход® состояние® выход, главное состояние.

В общем случае время в модели системы S может рассматриваться на интервале моделирования (0, T) как непрерывное, так и дискретное, т. е. квантованное на отрезки длиной D t временных единиц каждый, когда T= m D t, где 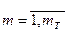— число интервалов дискретизации.

Таким образом, под математической моделью объекта (реаль­ной системы) понимают конечное подмножество переменных 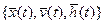вместе с математическими связями между ними и харак­теристиками .

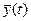Если математическое описание объекта моделирования не содержит элементов случайности или они не учитываются, то модель называется детерминированной в том смысле, что характеристики однозначно определяются детерминированными входными воздействиями

Если учитываются стохастические воздействия внешней среды 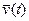 и стохастические внутренние параметры 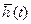, то это стохастическая модель.

 

Виды моделирования

ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ

При случае использования имитационных моделей в отличие от аналитических в ЭВМ воспроизводится текущее функционирование технической системы в некотором, удобном для пользователей, масштабе времени.

Входные воздействия воспроизводятся в виде наборов чисел – реализации процессов (а не числовых характеристик как при аналитическом моделировании).

Могут воспроизводиться также промежуточные преобразования обрабатываемого сигнала. В динамическом режиме работы имитационной модели может меняться корреляционная функция работы входных чисел с последующим отображением корреляции функции выходного сигнала.

Имитационное моделирование напоминает физический эксперимент (наглядность результатов моделирования, в том числе и промежуточных).

Достоинства имитационного моделирования:

1. возможность моделирования даже тогда, когда аналитические модели либо отсутствуют, либо (из-за сложности системы) не дают достоверных результатов (например перевод на разные языки, распознавание образов);

3. простота выработки управляющих воздействий на модель;

4. позволяет учесть влияние большого числа случайных и детерминированных факторов, а так же сложных зависимостей при вводе в модель соответствующих элементов и операций;

5. с точки зрения сбора статистических данных дает возможность проводить активный эксперимент с помощью целенаправленных изменений параметров модели на некотором множестве реализации, что позволяет оптимизировать модель.

При решении ряда задач могут применяться имитационные модели, отображающие только структурные, топологические (геометрические) свойства объектов. Такие структурные модели могут иметь форму:

1. матриц;

2. графов;

3. списка векторов

и выражать возможное расположение элементов в пространстве и их связи (провода, трубопроводы). Структурные модели используют в случаях, когда не учитываются физические процессы в объектах.

ФУНКЦИОНАЛЬНЫЕ МОДЕЛИ

При моделировании сложных технологических объектов возрастает объем входной информации (описание связей, задание параметров элементов модели, и т.д.). Укрупненность элементов модели приводит к возрастанию необходимой номенклатуры элементарных моделей, к увеличению объема моделирующей программы.

Компромисс - разбиение модели на функциональные блоки.

Функциональные модели отражают как структуру так и процессы функционирования объектов, и чаще всего имеют форму систем уравнений.

По способу получения функциональные модели делятся на:

- теоретические;

- формальные.

Формальные функциональные модели получают на основе проявления свойств моделируемого объекта во внешней среде. Они более точны в окрестности той точки пространства параметров, вблизи которой они определялись, но менее точны вдали от нее.

Глубина моделирования.

Моделируя сложные системы используют совокупность из нескольких моделей из числа всех разновидностей.

Любая система или подсистема может быть представлена различными способами, часто взаимодополняющими. В зависимости от глубины анализа простые модели заменяют все более сложные.

КОМБИНИРОВАННОЕ (АНАЛИТИКО-ИМИТАЦИОННОЕ) МОДЕЛИРОВАНИЕ

При построении комбинированной модели проводится предварительная декомпозиция (расчленение) процесса функционирования объекта на составляющие подпроцессы, и там, где это возможно используют аналитические модели, в остальных случаях – имитационные. Существует также так называемое натурное моделирование (производственный эксперимент, комплексные испытания) – проведение исследований на реальном объекте с последующей обработкой результатов эксперимента на основе теории подобия.