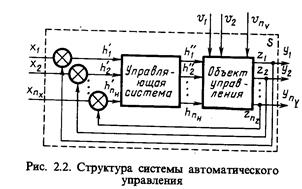
При описании процесса автоматического управления реальный объект представляют обычно в виде двух систем: управляющей и управляемой (объекта управления).
Структура САУ:
где эндогенные переменные:
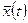 - векторы вх воздействий;
- векторы вх воздействий;
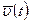 - векторы возмущающих воздействий;
- векторы возмущающих воздействий;
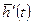 - векторы сигналов ошибки;
- векторы сигналов ошибки;
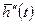 - векторы управляющих воздействий.
- векторы управляющих воздействий.
Экзогенные переменные:
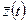 - вектор состояния системы
- вектор состояния системы 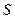 ;
;
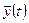 - вектор выходных переменных (обычно
- вектор выходных переменных (обычно 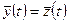 ).
).
Для одномерной системы ошибка управления системы 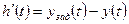 , где
, где 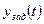 - заданный закон изменения управляемой величины системы;
- заданный закон изменения управляемой величины системы; 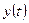 - действительный закон изменения.
- действительный закон изменения.
Если предписанный закон изменения управляемой величины соответствует закону изменения входного воздействия, т.е. 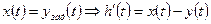 (при условии линейной зависимости
(при условии линейной зависимости 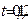 и
и 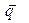 ).
).
Система управления называется идеальной, если 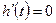 во все моменты времени. На практике это не возможно. Таким образом, ошибка
во все моменты времени. На практике это не возможно. Таким образом, ошибка 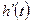 - неизбежная составляющая объекта автоматического управления, основанного на принципе отрицательной обратной связи. Т.к. для приведения в соответствие выходной переменной
- неизбежная составляющая объекта автоматического управления, основанного на принципе отрицательной обратной связи. Т.к. для приведения в соответствие выходной переменной 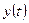 её заданному значению используется информация об отклонениями между ними.
её заданному значению используется информация об отклонениями между ними.
Задачей системы авт. управления является изменение переменной 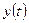 согласно заданному закону с определенной точностью (с допустимой ошибкой). При проектировании и эксплуатации систем авт. управления необходимо выбрать такие параметры системы
согласно заданному закону с определенной точностью (с допустимой ошибкой). При проектировании и эксплуатации систем авт. управления необходимо выбрать такие параметры системы 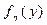 , которые обеспечили бы требуемую точность управления, а также устойчивость системы в переходном процессе.
, которые обеспечили бы требуемую точность управления, а также устойчивость системы в переходном процессе.
Если система устойчива, то представляют практический интерес поведение системы во времени, максимальное отклонение регулируемой переменной 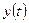 в переходном процессе, время переходного процесса, граничные условия.
в переходном процессе, время переходного процесса, граничные условия.
Свойства систем автоматического управления различных классов можно смоделировать с помощью дифференциальных уравнений и их коэффициентов. Порядок дифференциального уравнения и значения его коэффициентов полностью определяются статическими и динамическими параметрами системы 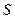 .
.
Пример:
Рассмотрим одноканальную систему автоматического управления SA, которая описывается 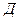 -схемой общего вида:
-схемой общего вида:
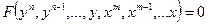 , (1)
, (1)
где 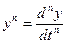 ;
; 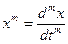
Пусть система SA, работает в некотором режиме малых отклонений от 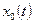 и
и 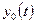 , т.е.
, т.е. 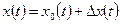 и
и 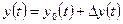 .
.
Тогда уравнение (1) можно линеаризовать, разложив функцию 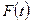 в ряд Тейлора и ограничиться его линейными членами относительно приращений
в ряд Тейлора и ограничиться его линейными членами относительно приращений 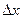 и
и 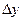 , т.е.:
, т.е.:
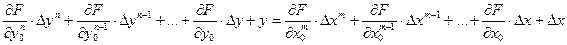 (2)
(2)
Т.к. уравнение (2) приблизительно описывает рассматриваемый процесс, то производные вычисляются при некоторых фиксированных значениях входящих в него переменных, т.е. мы получаем системы с постоянными коэффициентами.
Уравнения получаются линейными относительно 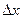 и
и 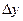 и их производных.
и их производных.
Методы решения и исследования линейной системы значительно проще, чем общего вида. Таким образом:
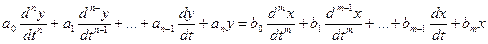 (3)
(3)
В уравнении (3) для простоты предполагается, что точка приложения возмущающих воздействий совпадает с входом системы (т.е. совпадает с начальной точкой). Решить это уравнение можно, например, операторным методом, значения ДУ алгебраическим (метод конечных разностей).
Таким образом, использование Д-схем позволяет формализовывать процесс функционирования непрерывно-детерминированных систем S и оценить их основные характеристики, применяя аналитический или имитационный подход.
12. ДИСКРЕТНО-ДЕТЕРМИНИРОВАННЫЕ МОДЕЛИ ( F-МОДЕЛИ)
Автомат можно представить как некоторое устройство, на которое подаются входные сигналы и снимаются выходные и которое может иметь некоторые внутренние состояния. Конечным автоматом называется автомат, у которого множество внутренних состояний и входных сигналов (а следовательно, и множество выходных сигналов) являются конечными множествами.
Абстрактно конечный автомат можно представить как математическую схему ( F-схему), характеризующуюся шестью элементами:
1) конечным множеством X входных сигналов (входным алфавитом);
2) конечным множеством Y выходных сигналов (выходным алфавитом);
3) конечным множеством Z внутренних состояний (внутренним алфавитом или алфавитом состояний);
4) начальным состоянием 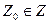 ;
;
5) функцией переходов 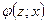 ;
;
6) функцией выходов 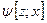 .
.
Автомат, задаваемый F-схемой: 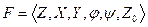 — функционирует в дискретном времени, такты, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния.
— функционирует в дискретном времени, такты, каждому из которых соответствуют постоянные значения входного и выходного сигналов и внутренние состояния.
Обозначим состояние, а также входной и выходной сигналы, соответствующие такту 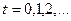 через
через 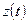 ,
, 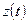 ,
, 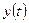 . При этом, по условию
. При этом, по условию 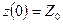 ,
, 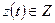 ,
, 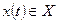 ,
, 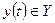 .
.
Абстрактный конечный автомат имеет один входной и один выходной каналы. В каждый момент 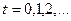 дискретного времени F-автомат находится в определенном состоянии
дискретного времени F-автомат находится в определенном состоянии 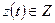 состояний автомата, причем в начальный момент времени
состояний автомата, причем в начальный момент времени 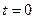 он всегда находится в начальном состоянии
он всегда находится в начальном состоянии 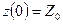 . В момент
. В момент 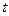 , будучи в состоянии z( t), автомат способен воспринять на входном канале сигнал
, будучи в состоянии z( t), автомат способен воспринять на входном канале сигнал 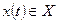 и выдать на выходном канале сигнал
и выдать на выходном канале сигнал 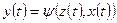 , переходя в состояние
, переходя в состояние 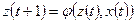 .
.
Если 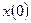 ,
, 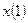 ,
, 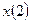 … - это входное, то
… - это входное, то 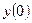 ,
, 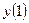 ,
, 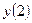 … - выходное слово.
… - выходное слово.
Таким образом, работа конечного автомата происходит по следующей схеме: в каждом 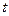 такте на вход автомата, находящегося в состоянии z( t), подается некоторый сигнал x( t), на который он реагирует переходом в
такте на вход автомата, находящегося в состоянии z( t), подается некоторый сигнал x( t), на который он реагирует переходом в 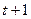 такте в новое состояние
такте в новое состояние 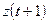 с выдачей некоторого выходного сигнала.
с выдачей некоторого выходного сигнала.
Получаем:
Для F-автомата первого рода (автомат Мили):
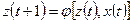
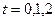
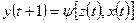
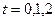
для F-автомата второго рода
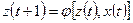
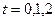
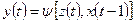
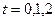
Автомат второго рода, для которого 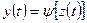 ,
, 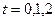 , т.е. функция выходов не зависит от входной переменной
, т.е. функция выходов не зависит от входной переменной 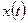 , называется автоматом Мура.
, называется автоматом Мура.
По числу состояний различают:
1) конечные автоматы с памятью
2) автоматы без памяти
По характеру отсчета дискретного времени конечные автоматы делятся на:
1) синхронные.
2) асинхронные - считывает входной сигнал непрерывно,
Чтобы задать конечный F-автомат, необходимо описать все элементы множества:
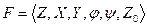 . При чем необходимо выделить
. При чем необходимо выделить 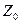 в момент
в момент 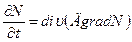 Существует несколько способов задания работы F-автомата, но наиболее часто используют табличный способ.
Существует несколько способов задания работы F-автомата, но наиболее часто используют табличный способ.
Табличный способ:
Строки соответствуют входным сигналам автомата, столбцы – его состояниям. Обычно первый слева столбец соответствует начальному состоянию z0 . На пересечении i-ой строки и k-го столбца таблицы переходов помещается соответствующее значение 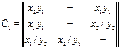 функции переходов, а в таблице выходов – соответствующее значение
функции переходов, а в таблице выходов – соответствующее значение 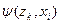 функции выходов.
функции выходов.
Для F-автоматов Мура обе таблицы можно совместить, получая отмеченную таблицу переходов, в которой над каждым состоянием 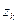 автомата, обозначающим столбец таблицы, стоит соответствующий этому состоянию выходной сигнал
автомата, обозначающим столбец таблицы, стоит соответствующий этому состоянию выходной сигнал 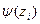 .
.
Таблица 1
|
|
| ||
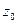
| 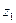
| ... 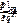
| |
| ПЕРЕХОДЫ | |||
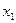
| 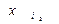
| 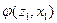
| ... 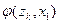
|
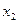
| 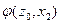
| 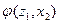
| ... 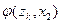
|
| ... | ... | ... | ... |
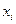
| 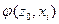
| 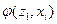
| ... 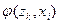
|
| ВЫХОДЫ | |||
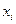
| 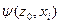
| 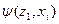
| ... 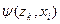
|
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ КОНЕЧНОГО АВТОМАТА, ЗАДАННОГО НАПРАВЛЕННЫМ ГРАФОМ
Граф автомата представляет собой набор вершин, соответствующих различным состояниям автомата и соединяющих вершины дуг графа, соответствующих тем или иным переходам автомата. Для автомата Мура аналогичная разметка графа такова: если входной сигнал xk, действуя на некоторое состояние автомата, вызывает переход в состояние zj то дугу, направленную в zj и помеченную xk, дополнительно отмечают выходным сигналом у = y ( zj, xk).
Таблица 2
| xi | zk | ||
| z0 | z1 | z2 | |
| Переходы | |||
| x1 | z2 | z0 | z0 |
| x2 | z0 | z2 | z1 |
| Выходы | |||
| x1 | y1 | y1 | y2 |
| x2 | y1 | y2 | y1 |
Таблица 3
| xi | y | ||||
| y1 | y1 | y3 | y2 | y3 | |
| z0 | z1 | z2 | z3 | z4 | |
| x1 | z1 | z4 | z4 | z2 | z2 |
| x2 | z3 | z1 | z1 | z0 | z0 |
На рис. 3, а, б приведены заданные ранее таблицами F-автоматы Мили F1 и Мура F2 соответственно.
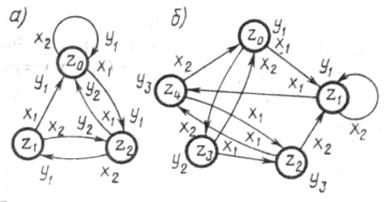
Рис. 3. Графы автоматов Мили (а) и Мура (6)
При решении задач моделирования систем часто более удобной формой является матричное задание конечного автомата. При этом матрица соединений автомата есть квадратная матрица С= ||с ij||, строки которой соответствуют исходным состояниям, а столбцы — состояниям перехода. Элемент cij = xk / ys, стоящий на пересечении i-й строки и j-го столбца, в случае автомата Мили соответствует входному сигналу xk, вызывающему переход из состояния zi в состояние zj, и выходному сигналу ys, вы даваемому при этом переходе. Для автомата Мили F1 матрица соединений имеет вид
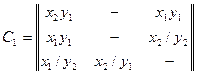 .
.
Если переход из состояния zi в состояние zj происходит под действием нескольких сигналов, элемент матрицы cij представляет собой множество пар «вход-выход» для этого перехода, соединенных знаком дизъюнкции.
Для F-автомата Мура элемент cij равен множеству входных сигналов на переходе (zi, zj), а выход описывается вектором выходов
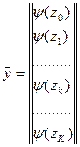
i-я компонента которого — выходной сигнал, отмечающий состояние zi.
Дата: 2018-11-18, просмотров: 330.