Стремятся отобразить лишь некоторую функцию, ту или иную связь между входами и выходами.

Аналитическая ММ представляется формулами, описывающими взаимозависимость параметров (входные, состояние внешней среды, выходные).

Аналитическая модель может исследоваться:

1. аналитическими методами получают в общем виде явные зависимости для искомых величин;

2. численными методами – когда не имея решений уравнения в общем виде применяют средства вычислительной техники для получения числовых результатов с конкретными начальными данными;

3. качественно – когда не имея решения в явном виде можно найти некоторое свойство решений (например, оценить устойчивость решения).

Мысленное моделирование часто является единственным способом объектов, которые либо практически не реализуемы в заданном интервале времени, либо существуют вне условий, возможных для их физического создания.

Мысленное моделирование может быть реализовано в виде наглядного, символического, математического.

В наглядном моделировании на базе представления человека о реальных объектах создаются различные наглядные модели, отображающие явления и процессы, протекающие в объекте.

В основу гипотетического моделирования закладывается гипотеза о закономерностях протекания процессов в реальном объекте. Символическое моделирование представляет собой искусственный процесс создания логического объекта, заменяющего реальный и выражающий основные свойства.

Языковое моделирование – в основе лежит понятие тезауруса, который образуется из набора фиксированных входящих понятий. Тезаурус – словарь, очищенный от неоднозначностей.

Математические модели объектов проектирования, используемых на микроуровне.

отражают физические процессы, протекающие в сплошных средах и непрерывном времени. Назовём независимыми переменными координаты x, y, z и t – время.

Зависимые, фазовые переменные: E – напряженность электрического поля; U – напряжение; N – концентрация частиц; H – напряженность магнитного поля; деформации, либо после деформации в механике.

Основу математических моделей на микроуровне составляют интегральные, интегро-дифференциальные и дифференциальные уравнения частных производных.

УСЛОВИЯ ДЛЯ ПОСТРОЕНИЯ ЗАКОНЧЕННОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ

1. выбрать краевые условия, представляющие собой сведения о значениях фазовых переменных и их производных на границе рассматриваемых областей.

2. дискретизация задачи, т.е. разделение рассматриваемых пространственных и временных областей на дискреты – конечное число элементарных участков значений фазовых переменных в избранных узловых точках.

3. алгебраизация задачи – аппроксимация дифференциальных и интегральных уравнений алгебраически.

Для дискретизации и алгебраизации краевых задач используют два основных подхода:

1. метод конечных разностей (МКР)

2. метод конечных элементов (МКЭ)

Обобщенная форма записи ДУ объекта микроуровня:

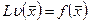 или ,

где L – дифференциальный оператор 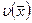,  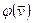- зависимая фазовая переменная (U, E, H, …)

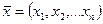 - векторы независимых пространственных координат

 - заданная функция

Нестационарное уравнение в операторной форме можно записать:

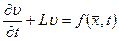
или

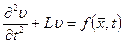
где 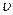 - функция координат  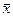и времени .

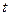Например, для двумерного уравнения диффузии:

,

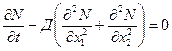- концентрация примеси

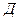- коэффициент диффузии

Т.е. это уравнение показывает, что изменение концентрации движущихся в сплошной среде носителей ( 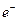и дырок 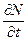) будет равна коэффициенту диффузии на 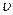измерения концентрации примеси по координатам  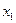и .

В данном случае мы использовали запись:

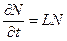, где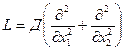

Применяется так же более короткая форма записи нестационарных уравнений в виде:

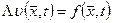
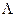 - дифференциальный оператор, включающий дифференцирование по всем независимым переменным.

Математическая модель, описываемая этим уравнением должна содержать также краевые условия. Для диффузии краевыми условиями существования ограниченной области может быть условленная min концентрация заряженных частиц.

Краевые условия состоят из граничных и начальных условий. Для граничных условий задаётся , где  - граница рассматриваемой пространственной области.

Для начальных условий задаётся .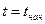

9. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДИФФУЗНЫХ ЯВЛЕНИЙ В ПОЛУПРОВОДНИКАХ

Каждому типу природных взаимодействий можно подобрать более или менее адекватную ММ. Явление диффузии электронов и дырок в полупроводниках – пример наиболее простых и характерных взаимодействий на микроуровне. Уравнение непрерывности Пуассона выражает в полупроводниках скорости изменения концентрации свободных носителей заряда и записывается отдельно для электронов и дырок.

 (1)

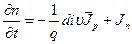 (2)

где 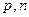 - концентрация дырок и электронов

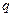 - заряд

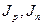 - скорости процесса инерции-рекомбинации электронов и дырок

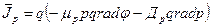 - плотность дырочного тока (3)

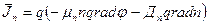 - плотность электронного тока (4)

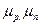 - подвижности электронов и дырок

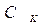 - коэффициенты диффузии дырок и электронов

 - потенциал

Уравнения 1-2 показывают, что причинами изменения концентрации носителей может быть неодинаковость числа носителей, втекающих (и вытекающих) в элементарный объём полупроводника.

Тогда 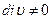 и наблюдается нарушение равновесия между процессами генерации и рекомбинации носителей.

Уравнения (3) и (4) называются уравнениями плотности тока, характеризуют причины протекания электрического тока в полупроводниках, электрический дрейф под воздействием электрического поля 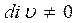 и диффузию носителей при наличии градиента концентрации.

Уравнение Пуассона характеризует зависимость изменений в пространстве напряженности электрического поля 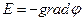 от распределения плотности электрических зарядов 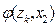, тогда ,

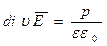где 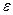 - относительная диэлектрическая проницаемость,  - диэлектрическая постоянная

В качестве краевых условий в моделях полупроводниковых приборов используют зависимости потенциалов на контактах от 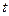. В основе модели диффузионных процессов лежит уравнение диффузии: ,

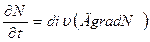где  - концентрация примесей, 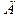 - коэффициент диффузии.

Краевые условия представлены зависимостью распределения примесей  в объёме полупроводника в некоторый момент времени и зависимостью поверхностной концентрации от .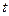

Всё это – математические схемы общего вида, но на практике на первоначальных этапах исследования используют типовые математические схемы.