1) Длина вектора. Применяя формулу (2.3) при 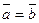, имеем 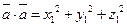. С другой стороны 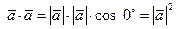. Отсюда получаем формулу для определения длины вектора

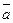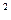
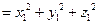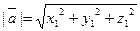| | или                             (2.4)

2) Расстояние между двумя точками в пространстве. Рассмотрим следующую задачу. Даны две точк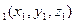и M и M 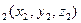. Найти расстояние между ними.

      Z

  ^О                        Y

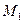
Заметим, что вектор 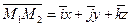 есть разность векторов

.

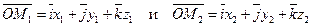Таким образом, 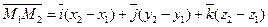. Следовательно, 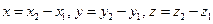. Применяя формулу (1.4), получим

.

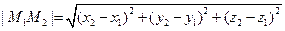Пример 2.1. Определить расстояние между точкам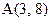и  и .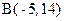

Решение. Воспользовавшись формулой (2.2), получим

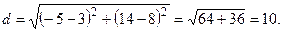
3) Угол между двумя векторами. Рассмотрим задачу об определении угла между двумя векторами. Согласно определению скалярного произведения векторов, имеем: 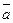∙ 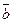= | |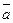| | 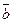cosj, где j — угол между векторам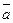и  и 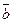. Из этой формулы находим

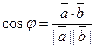                                                                                            (2.5)

Выражая числитель и знаменатель в проекциях, получим формулу для вычисления угла между двумя данными векторами

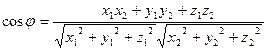.                                              (2.6)

4) Направление вектора. Пусть a, b и g — углы, образованные вектором 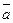 с осями координат OX, OY и OZ соответственно. Имеем 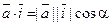. Отсюда

.

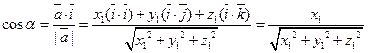Аналогично получим

;        .

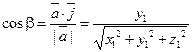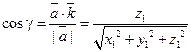Величины cosa, cosb, cosg называются направляющими косинусами вектора 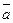. Имеет место очевидное равенство: .

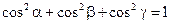5) Деление отрезка в заданном отношении. Пусть даны точки A( 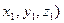и B( 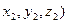. Будем говорить, что точка M(x,y,z) делит отрезок  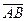в заданном отношении l, если .

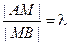                                          B

                        M

       A

                   O                                      

Требуется найти координаты точки M, делящей отрезок 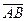 в отношении l.

По условию имеем 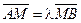. Обозначим через  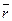— радиус-вектор точки M,  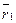— радиус вектор точки A,  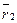— радиус вектор точки B. Замечая, что 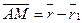, а 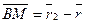, перепишем (2.7) в виде .

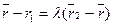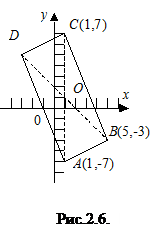Отсюда имеем :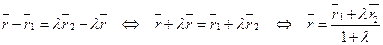   

или в координатах:           .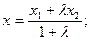

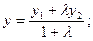
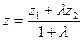В частности координаты середины отрезка: .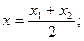

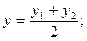
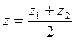Пример 2.2. Даны три вершины 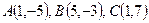параллелограмма 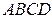. Найти его четвертую вершину D.

Решение.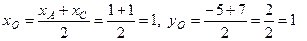

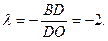
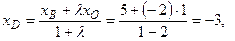
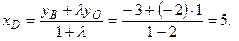
2.1.9. Преобразование координат при параллельном переносе осей координат

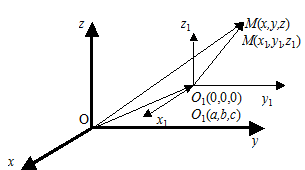Пусть система координат О₁x₁y₁z₁ получается из системы Оxyz параллельным переносом осей координат, причем координаты нового начала координат О₁ переносятся в точку с координатами (a,b,c). Из правил действий над векторами получаем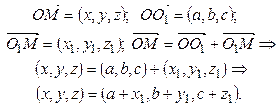

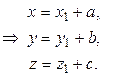
ЛИТЕРАТУРА

Для содержательных модулей

1. Ильин В.А., Позняк Э.Г. Линейная алгебра. — М.: Наука, 1978.

2. Кудрявцев Л.Д. Курс математического анализа. Т. 1-3. — М.: Высш.шк., 1981.

Основная

1. Высшая математика для экономистов: Учебник для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ, 2003.

2. Колесников А.Н. Краткий курс математики для экономистов. — М.: Инфра-М, 1997.

3. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. — М.: Финансы и статистика, 2003.

4. Ляшенко И.Н., Ляшенко Е.И. Математика для экономистов: Учебное пособие для подготовки бакалавров экономического профиля. — 1998.

5. Практикум по высшей математике для экономистов: Учебное пособие для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ-ДАНА, 2004.

6. Гусак А.А. Пособие к решению задач по высшей математике. — Минск, 1968.

7. Руководство к решению задач с экономическим содержанием по курсу высшей математики./ Под ред. А.И. Карасева и Н.Ш. Кремера. — М.: Экономическое образование, 1989.

8. Данко П.Е., Попова А.Г. Высшая математика в упражнениях и задачах. — М.: Высш.шк., 1974.

Сборники задач

1. Минорский В.П. Сборник задач по высшей математике. — М.: Наука, 1977.

2. Проскуряков И.В. Сборник задач по линейной алгебре. — М.: Наука, 1967.

3. Берман Г.Н. Сборник задач по курсу математического анализа. — М.: Наука, 1977.