Лекция 3. Векторы.
Вопросы:
1. Понятие векторов и линейные действия с ними.
2. Векторные линейные пространства.
3. Скалярное и векторное произведение векторов.
4. Экономические примеры.
5. Линейная зависимость и независимость векторов.
6. Базис. Разложение вектора по базису.
7. Ортогональные системы векторов.
8. Переход от одного базиса к другому.
9. Длина вектора.
10. Угол между векторами.
11. Расстояние между двумя точками.
12. Коллинеарность и компланарность векторов.
Помимо матриц и определителей есть еще одно важное математическое понятие, широко применяемое в приложениях и имеющее общематематический интерес, а именно, понятие n-мерного вектора.
Из курса аналитической геометрии известно, что каждый вектор на плоскости R2 можно задать упорядоченной парой чисел (x1, x2) – его координатами, а в пространстве R3 упорядоченной тройкой чисел (x1, x2, x3). В экономической практике встречаются объекты, для описания которых недостаточно трех чисел, например, запасы имеющихся ресурсов производства, объемы выпуска различных видов продукции и т.д. Рассмотрим распределение дохода предприятия:
x1 — плата за производственные ресурсы;
x2 — плата за природные ресурсы;
x3 — фонд оплаты труда;
x4 — фонд социального развития;
x5 — фонд развития производства;
x6 — отчисления в местный бюджет и виде налогов;
x7 — отчисления в республиканский бюджет в виде налогов. Распределение дохода предприятия можно записать в виде семимерного вектора
(x1, x2, x3, x4, x5, x6, x7).
Если известно, что x1=18%, x2=2%, x3=40%, x4=7%, x5=13%, x6=6%, x7=14%, тогда распределение дохода предприятия есть вектор
(18; 2; 40; 7; 13; 6; 14).
Определение 1.20. Упорядоченная система из п чисел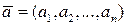 
называется п-мерным вектором. Числа 
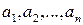называются координатами вектора 
.
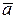Пример 1.25. Пусть набор значений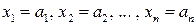 
является решением системы (1.6). Это решение можно записать как n-мерный вектор 
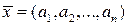. Набор значений свободных членов 
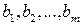можно рассматривать как m-мерный вектор 
.
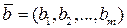Определение 1.21. Векторы равны, если равны их соответствующие координаты.
Определение 1.22. Суммой векторов 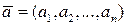и 
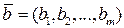называется вектор 
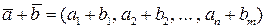, координаты которого есть суммы соответствующих координат векторов 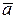и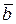 
.
Определение 1.23. Произведением вектора 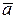на число k называется вектор 
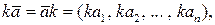координаты которого равны произведению k и соответствующих координат вектора .
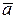Определение 1.24. Вектор, у которого все координаты равны нулю, называется нулевым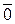 
= (0,0,...,0).
Определение 1.25. Вектор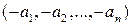 
называется противоположным вектору 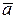и обозначается - 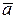. Очевидно, что 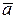+ (- 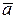) = 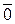. Таким образом, для сложения векторов существует обратная операция.
Определение 1.26. Разностью векторов 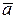и 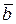называется вектор
.
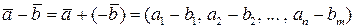Определение 1.27. Совокупность всех n-мерных векторов с действительными координатами, для которых определены операции сложения векторов и умножения вектора на число, называется арифметическим п-мерным векторным пространством и обозначается Rn.
Определение 1.28. Евклидовым пространством называется n-мерное векторное пространство, в котором введена операция скалярного произведения векторов. Его обозначают Еn.
Если координаты векторов известны, то скалярное произведение определяется равенством: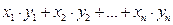 
, скалярное произведение векторов это число (скаляр).
Введенные определения записываются в следующем виде:
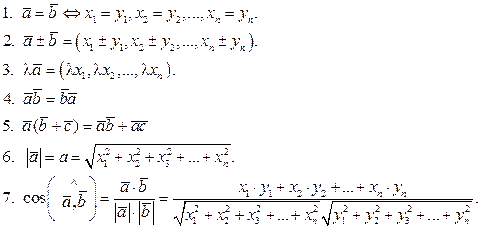(1.16)
Определение 1.29.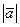 
называется длиной или модулем вектора 
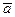, если 
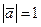, то такой вектор называют ортом.
Определение 1.30. Если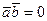 
, то векторы называются ортогональными.
Пример 1.26. Даны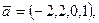 
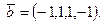
Найти: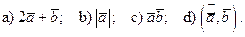 
Решение.
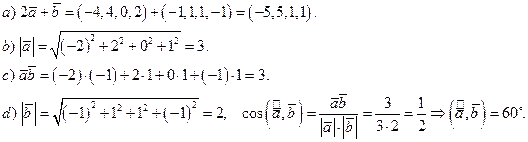
Элементы векторной алгебры
Определение 2.4. Отрезок, имеющий заданные длину и направление в пространстве называется вектором.
A
O
Определение 2.5. Два вектора считаются равными, если выполнены условия:
а) длины векторов равны;
б) векторы коллинеарны, (т. е. расположены на одной прямой или на параллельных прямых);
в) векторы имеют одинаковое направление.
Следует различать начало и конец вектора. Поменяв их местами, мы получим уже другой вектор, направленный противоположно исходному.
А О
О А
Из определения равенства векторов следует, что при параллельном переносе вектора получаем вектор, равный исходному. Поэтому начало вектора можно помещать в любой точке пространства. Вектор с началом в точке O и концом в точке M обозначим символом 
или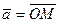 
. Длину вектора 
обозначим | | или |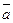 
|. Вектор, у которого начало совпадает с концом, называется нулевым вектором.
Определение 2.6. Два вектора,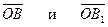 
, имеющие равные длины, но противоположно направленные, называются противоположными векторами. Сумма их равна нулевому вектору.
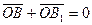
B O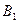 
Вектор противоположный вектору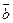 
будем обозначать 
.
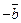ЛИТЕРАТУРА
Для содержательных модулей
1. Ильин В.А., Позняк Э.Г. Линейная алгебра. — М.: Наука, 1978.
2. Кудрявцев Л.Д. Курс математического анализа. Т. 1-3. — М.: Высш.шк., 1981.
Основная
1. Высшая математика для экономистов: Учебник для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ, 2003.
2. Колесников А.Н. Краткий курс математики для экономистов. — М.: Инфра-М, 1997.
3. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. — М.: Финансы и статистика, 2003.
4. Ляшенко И.Н., Ляшенко Е.И. Математика для экономистов: Учебное пособие для подготовки бакалавров экономического профиля. — 1998.
5. Практикум по высшей математике для экономистов: Учебное пособие для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ-ДАНА, 2004.
6. Гусак А.А. Пособие к решению задач по высшей математике. — Минск, 1968.
7. Руководство к решению задач с экономическим содержанием по курсу высшей математики./ Под ред. А.И. Карасева и Н.Ш. Кремера. — М.: Экономическое образование, 1989.
8. Данко П.Е., Попова А.Г. Высшая математика в упражнениях и задачах. — М.: Высш.шк., 1974.
Сборники задач
1. Минорский В.П. Сборник задач по высшей математике. — М.: Наука, 1977.
2. Проскуряков И.В. Сборник задач по линейной алгебре. — М.: Наука, 1967.
3. Берман Г.Н. Сборник задач по курсу математического анализа. — М.: Наука, 1977.
Лекция 3. Векторы.
Вопросы:
1. Понятие векторов и линейные действия с ними.
2. Векторные линейные пространства.
3. Скалярное и векторное произведение векторов.
4. Экономические примеры.
5. Линейная зависимость и независимость векторов.
6. Базис. Разложение вектора по базису.
7. Ортогональные системы векторов.
8. Переход от одного базиса к другому.
9. Длина вектора.
10. Угол между векторами.
11. Расстояние между двумя точками.
12. Коллинеарность и компланарность векторов.
Помимо матриц и определителей есть еще одно важное математическое понятие, широко применяемое в приложениях и имеющее общематематический интерес, а именно, понятие n-мерного вектора.
Из курса аналитической геометрии известно, что каждый вектор на плоскости R2 можно задать упорядоченной парой чисел (x1, x2) – его координатами, а в пространстве R3 упорядоченной тройкой чисел (x1, x2, x3). В экономической практике встречаются объекты, для описания которых недостаточно трех чисел, например, запасы имеющихся ресурсов производства, объемы выпуска различных видов продукции и т.д. Рассмотрим распределение дохода предприятия:
x1 — плата за производственные ресурсы;
x2 — плата за природные ресурсы;
x3 — фонд оплаты труда;
x4 — фонд социального развития;
x5 — фонд развития производства;
x6 — отчисления в местный бюджет и виде налогов;
x7 — отчисления в республиканский бюджет в виде налогов. Распределение дохода предприятия можно записать в виде семимерного вектора
(x1, x2, x3, x4, x5, x6, x7).
Если известно, что x1=18%, x2=2%, x3=40%, x4=7%, x5=13%, x6=6%, x7=14%, тогда распределение дохода предприятия есть вектор
(18; 2; 40; 7; 13; 6; 14).
Определение 1.20. Упорядоченная система из п чисел 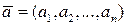называется п-мерным вектором. Числа 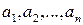называются координатами вектора .
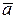Пример 1.25. Пусть набор значений 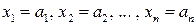является решением системы (1.6). Это решение можно записать как n-мерный вектор 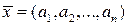. Набор значений свободных членов 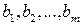можно рассматривать как m-мерный вектор .
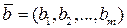Определение 1.21. Векторы равны, если равны их соответствующие координаты.
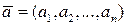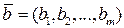Определение 1.22. Суммой векторов и называется вектор 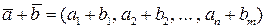, координаты которого есть суммы соответствующих координат векторов 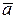и .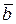
Определение 1.23. Произведением вектора 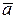на число k называется вектор 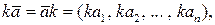координаты которого равны произведению k и соответствующих координат вектора .
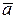Определение 1.24. Вектор, у которого все координаты равны нулю, называется нулевым 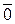= (0,0,...,0).
Определение 1.25. Вектор 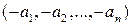называется противоположным вектору 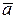и обозначается - 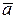. Очевидно, что 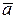+ (- 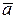) = 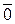. Таким образом, для сложения векторов существует обратная операция.
Определение 1.26. Разностью векторов 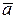и 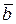называется вектор
.
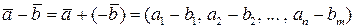Определение 1.27. Совокупность всех n-мерных векторов с действительными координатами, для которых определены операции сложения векторов и умножения вектора на число, называется арифметическим п-мерным векторным пространством и обозначается Rn.
Определение 1.28. Евклидовым пространством называется n-мерное векторное пространство, в котором введена операция скалярного произведения векторов. Его обозначают Еn.
Если координаты векторов известны, то скалярное произведение определяется равенством: 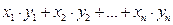, скалярное произведение векторов это число (скаляр).
Введенные определения записываются в следующем виде:
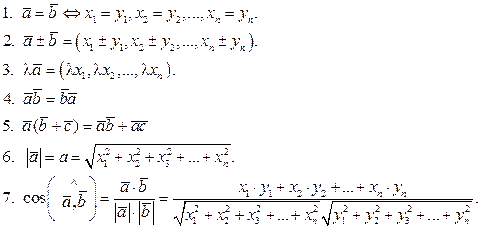(1.16)
Определение 1.29. 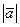называется длиной или модулем вектора 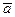, если 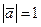, то такой вектор называют ортом.
Определение 1.30. Если 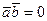, то векторы называются ортогональными.
Пример 1.26. Даны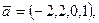
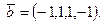
Найти: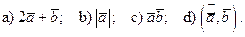
Решение.
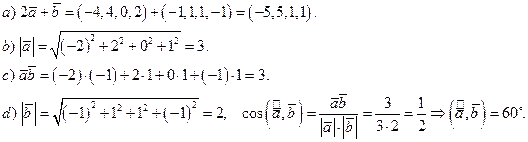
Линейная зависимость векторов
Обобщением понятий коллинеарности и компланарности векторов служит следующее понятие.
Определение 1.31. Вектор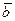 
называется линейной комбинацией векторов 
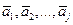, если существуют числа 
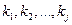такие, что
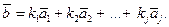
Определение 1.32. Система векторов 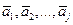линейно зависима, если один из векторов является линейной комбинацией других векторов этой системы, и линейно независима в противном случае.
Теорема 1. Система векторов 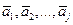линейно зависима, если существуют числа 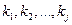(хотя бы одно из которых отлично от нуля) такие, что
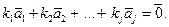
Пример 1.27. Векторы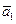 
= (1,2,1), 
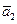= (1,1,0), 
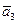= (0,1,4) линейно независимы.
Действительно, запишем равенство
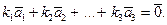
Если записать это векторное равенство в координатной форме, приходим к системе
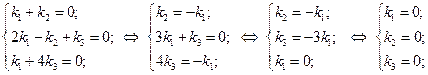
Система определенная и имеет единственное решение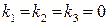 
, т.е. векторы 
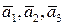— линейно независимы.
Теорема 3. Любая система из п+1 векторов в п-мерном векторном пространстве линейно зависима.
Из теорем 2 и 3 следует, что в пространстве Rn максимальное число линейно независимых векторов равно n .
Определение 1.33. Максимальное число линейно независимых векторов называется размерностью векторного пространства.
Таким образом, пространство Rn имеет размерность п. Поэтому оно называется арифметическим п-мерным векторным пространством. В частности, совокупность векторов плоскости образует арифметическое двумерное векторное пространство R2, а совокупность векторов пространства — арифметическое трехмерное пространство R3.
Определение 1.34. Любые п линейно независимых векторов п-мерного векторного пространства называются его базисом.
Ортогональные векторы всегда линейно независимы, поэтому в приложениях чаще всего применяют ортогональный или ортонормированный базис (ортогональный базис, все векторы которого имеют единичную длину).
Таким образом, число векторов базиса совпадает с его размерностью. Одним из базисов пространства Rn являются векторы
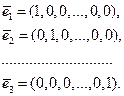
Система векторов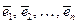 
является ортогональным и ортонормированным базисом.
Заметим, что кроме указанного базиса в п-мерном векторном пространстве существует бесконечное число других базисов. Так, например, одним из них является базис, образованный векторами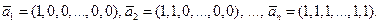 
В самом деле, равенство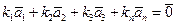 
справедливо только при 
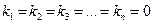, так как из эквивалентной ему системы n уравнений для координат данных векторов
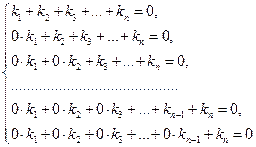
следует, что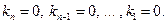 
Итак, векторы 
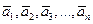линейно независимы и, следовательно, образуют базис в Rn.
Теорема 4. Пусть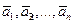 
— некоторый базис в n-мерном векторном пространстве, тогда в разложении любого вектора 
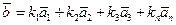коэффициенты 
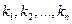определяются единственным образом.
Числа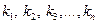 
называются координатами вектора в данном базисе.
Теорема 5. Для того, чтобы векторы 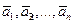образовывали базис в n-мерном векторном пространстве Rn, необходимо и достаточно, чтобы определитель, составленный из координат этих векторов, был не равен нулю.
Пример 1.28. Определить ранг и некоторый базис системы векторов на плоскости.
Решение. Ранг данной, системы состоящей из семи векторов на плоскости равный двум. Базис образовывают два произвольных не коллинеарных вектора. Пары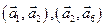 
образуют базис этой системы, а пары 
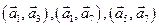не образуют базис.
Пример 1 .29. Проверить, что векторы
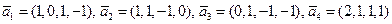
образуют базис R4. Найти разложение вектора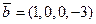 
по данному базису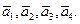 
Решение. Составим определитель из координат векторов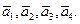
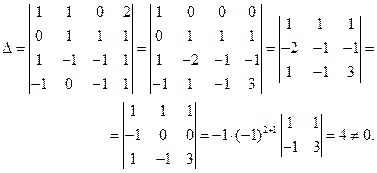
Следовательно,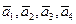 
образуют базис в 
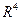. Найдем разложение вектора 
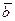в этом базисе. Векторное уравнение 
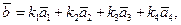равносильно следующей системе линейных уравнений
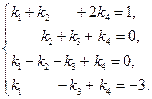
Решим систему методом Гаусса, выполняя элементарные преобразования над расширенной матрицей
Отсюда последовательно находим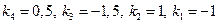 
— координаты вектора 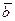в данном базисе. Итак, разложение вектора 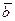по данному базису имеет вид 
.
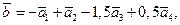1.6.3. Линейные преобразования. Собственные векторы и числа
Определение 1.35. Линейным преобразованием n-мерного вектора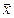 
в m-мерный вектор 
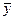называется преобразование, которое определяется матрицей 
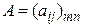по формуле: 
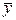=А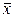 
. Матрица А называется оператором линейного преобразования.
Для линейных операторов
.
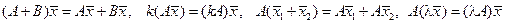Определение 1.36. Пусть А: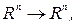 
тогда вектор х называется собственным вектором оператора А, если АХ=λх, λ≠0, а число λ называется собственным значением (числом) оператора А.
Все собственные значения являются корнями уравнения det(A-λE)=0.
Пример 1.30. Найти собственные значения и собственные векторы оператора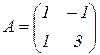 
.
Решение.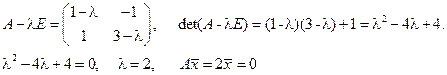 
Дата: 2018-11-18, просмотров: 325.
