Пусть задана прямоугольная матрица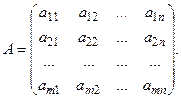

Выделим в этой матрице k произвольных строк и k произвольных столбцов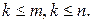

Определение 1.13. Определитель k-ro порядка, составленный из элементов матрицы A, расположенных на пересечении выделенных строк и столбцов, называется минором k-ro порядка матрицы A.

Рассмотрим всевозможные миноры матрицы А, отличные от нуля.

Определение 1.14. Рангом матрицы А называется наибольший порядок минора этой матрицы, отличного от нуля. Если все элементы матрицы равны нулю, то ранг этой матрицы принимают равным нулю.

Всякий отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется базисным минором матрицы,

Ранг матрицы А будем обозначать через r(А), 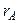. Если 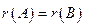, то матрицы A и В называются эквивалентными. В этом случае пишут A ~ В.

Полезно иметь в виду, что ранг матрицы не изменяется при элементарных преобразованиях.

Элементарные преобразования матрицы частично совпадают с элементарными преобразованиями определителей. К ним относятся:

1) умножение всех элементов какой-либо строки (столбца) матрицы на одно и то же число, отличное от нуля;

2) прибавление к элементам какой-либо строки (столбца) матрицы соответствующих элементов другой строки (столбца);

3) перемена местами строк (столбцов) матрицы;

4) отбрасывание строк (столбцов) матрицы, все элементы которых равны нулю.

Пример 1.16. Определить ранг матрицы .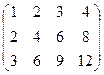

Решение. Все миноры второго и третьего порядков данной матрицы равны нулю, так как элементы строк этих миноров пропорциональны. Миноры же первого порядка (сами элементы матрицы) отличны от нуля. Следовательно, ранг матрицы равен 1.

Пример 1.17. Определить ранг матрицы .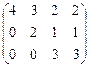

Решение. Вычтем из элементов 4-го столбца элементы 3-го столбца

 Вычеркнем 4-й столбец .

Так как 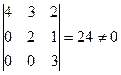, то ранг матрицы равен трем.

ЛИТЕРАТУРА

Для содержательных модулей

1. Ильин В.А., Позняк Э.Г. Линейная алгебра. — М.: Наука, 1978.

2. Кудрявцев Л.Д. Курс математического анализа. Т. 1-3. — М.: Высш.шк., 1981.

Основная

1. Высшая математика для экономистов: Учебник для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ, 2003.

2. Колесников А.Н. Краткий курс математики для экономистов. — М.: Инфра-М, 1997.

3. Солодовников А.С., Бабайцев В.А., Браилов А.В. Математика в экономике. — М.: Финансы и статистика, 2003.

4. Ляшенко И.Н., Ляшенко Е.И. Математика для экономистов: Учебное пособие для подготовки бакалавров экономического профиля. — 1998.

5. Практикум по высшей математике для экономистов: Учебное пособие для вузов/ Под ред. Н.Ш. Кремера. — М.: ЮНИТИ-ДАНА, 2004.

6. Гусак А.А. Пособие к решению задач по высшей математике. — Минск, 1968.

7. Руководство к решению задач с экономическим содержанием по курсу высшей математики./ Под ред. А.И. Карасева и Н.Ш. Кремера. — М.: Экономическое образование, 1989.

8. Данко П.Е., Попова А.Г. Высшая математика в упражнениях и задачах. — М.: Высш.шк., 1974.

Сборники задач

1. Минорский В.П. Сборник задач по высшей математике. — М.: Наука, 1977.

2. Проскуряков И.В. Сборник задач по линейной алгебре. — М.: Наука, 1967.

3. Берман Г.Н. Сборник задач по курсу математического анализа. — М.: Наука, 1977.