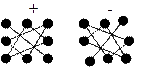Пусть А — матрица нормозатрат второго порядка:
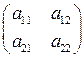
На практике запасы сырья ограничены. Обозначим 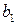 запас сырья
запас сырья 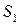 и
и 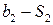 , если
, если 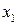 и
и 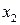 — объемы производства продуктов
— объемы производства продуктов 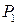 и
и 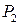 соответственно, то
соответственно, то 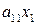 — затраты
— затраты 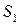 на производство
на производство 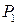 ,
, 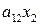 — затраты
— затраты 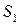 на производство
на производство 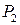 ,
, 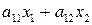 — суммарные затраты
— суммарные затраты 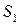 ; соответственно
; соответственно 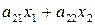 — суммарные затраты сырья
— суммарные затраты сырья 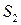 на производство
на производство 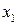 единиц продукции
единиц продукции 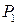 и
и 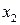 единиц продукции
единиц продукции 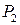 . Должны быть выполнены следующие условия, называемые балансовыми уравнениями:
. Должны быть выполнены следующие условия, называемые балансовыми уравнениями:
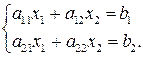
Решение этой системы дает возможность найти допустимые объемы производства продуктов при наличии данных запасов сырья. Домножим первое уравнение на 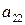 , а второе — на
, а второе — на 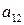 и сложим, получим
и сложим, получим
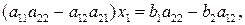
аналогичным образом, исключая 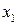 :
:
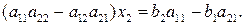
В результате коэффициенты при 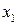 и
и 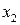 совпадают и составлены из элементов матрицы А по следующему правилу: от произведения элементов главной диагонали вычитается произведение элементов побочной диагонали.
совпадают и составлены из элементов матрицы А по следующему правилу: от произведения элементов главной диагонали вычитается произведение элементов побочной диагонали.
Это число называется определителем матрицы А и обозначается
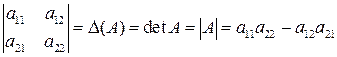 .
.
Определители можно рассматривать и вне связи с исходной матрицей, тогда эту формулу называют определителем второго порядка. Аналогично можно ввести определители третьего порядка.
Таким образом, определитель — число, характеризирующее квадратную матрицу и тесно связанное с решением систем линейных уравнений. Определитель матрицы А обозначается 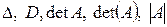 .
.
Определение 1.5. Определителем матрицы первого порядка 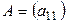 , называется само число
, называется само число 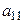 :
: 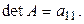 Например,
Например, 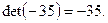
Определение 1 .6. Определителем матрицы второго порядка 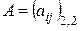 , или определителем второго порядка, называется число, которое вычисляется по формуле
, или определителем второго порядка, называется число, которое вычисляется по формуле
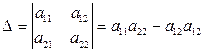
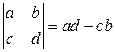 . (1.1)
. (1.1)
Числа а, d образуют главную диагональ; числа с, b образуют побочную диагональ.
Пример 1.7. Вычислить определитель второго порядка.
Решение. 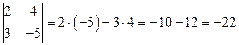 .
.
Определение 1.7. Определителем матрицы третьего порядка 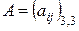 , или определителем третьего порядка называется число, которое вычисляется по формуле
, или определителем третьего порядка называется число, которое вычисляется по формуле
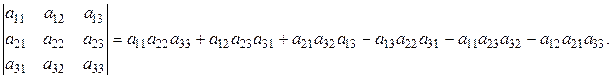 (1.2)
(1.2)
Каждое произведение 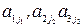 : называется членом определителя, где
: называется членом определителя, где 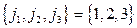
Из равенства (1.2) следует, что каждый член правой части равен произведению трех элементов определителя, взятых по одному из каждой строки и каждого столбца. Чтобы запомнить, какие произведения берутся со знаком «плюс», а какие со знаком «минус», полезно запомнить следующее правило треугольников:
|
Пример 1.8. Вычислить определитель третьего порядка:
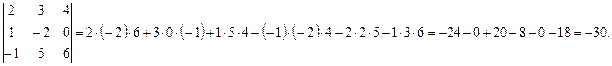
Для вычисления определителей третьего порядка удобно пользоваться следующим методом. Справа дописывают два первых столбца, а потом делают вычисления, как показано на схеме (правило Саррюса):
+ -






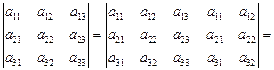
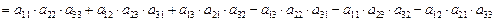 .
.
Пример 1.9. Вычислить определитель третьего порядка:
+ -






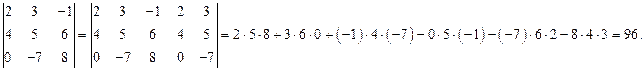
Дата: 2018-11-18, просмотров: 322.