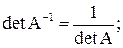Теорема 1. Каждый определитель можно представить как сумму произведений элементов любой строки (столбца) на соответствующие им алгебраические дополнения.
Теорема 2. Сумма произведений элементов любой строки (столбца) на алгебраические дополнения элементов другой строки (столбца) равна нулю.
Пример 1.11. Вычислить определитель разложением по первой строкой.
Решение.
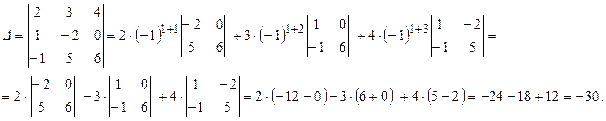
1.2.5. Понятие определителя n-го порядка. Вычисление определителей n-го порядка
Определение 1.10. Определителем квадратной матрицы n-го порядка  , или определителем n-го порядка, называется число
, или определителем n-го порядка, называется число
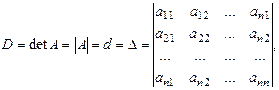 (1.4)
(1.4)
При вычислении определителей высших порядков, как правило, пользуются свойствами определителей. В частности, с помощью теоремы 1 вычисление определителя n-го порядка сводится к вычислению определителей n-1-го порядка, вычисление определителя n-1-го порядка сводится к вычислению определителей n-2-го порядка и т. д., пока не дойдем до определителей второго или даже первого порядка.
Пример 1.12. Вычислить определитель  .
.
Решение. Разложим определитель по третьему столбцу
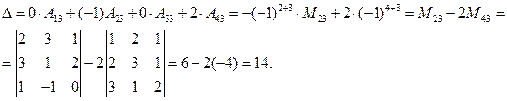
В примере 1.12 количество элементов уменьшилось, поскольку использовали столбец, содержащий нули.
Пример 1.13. Вычислить определитель пятого порядка 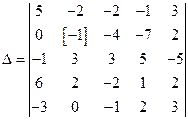 .
.
Решение. Чтобы упростить вычисления, проведем дополнительные преобразования, используя свойство 7.
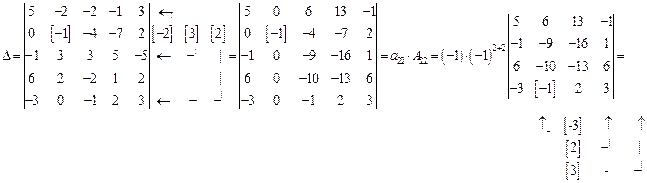

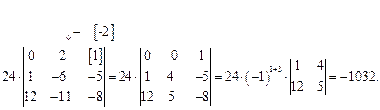
ОБРАТНАЯ МАТРИЦА. НАХОЖДЕНИЕ ОБРАТНОЙ МАТРИЦЫ
Определение 1 11. Квадратную матрицу А называют невырожденной или неособенной, если 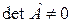 . Если
. Если 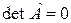 , то А — особая или вырожденная.
, то А — особая или вырожденная.
Определение 1 12. Матрица А-1 называется обратной к квадратной матрице А, если при умножении этой матрицы на данную матрицу как справа, так и слева получается единичная матрица: 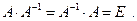
Для каждой невырожденной матрицы существует обратная матрица, она находится по формуле
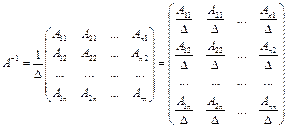
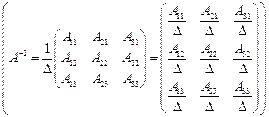 , (1.5)
, (1.5)
где Аij – алгебраическое дополнение к элементу aij. Алгебраические дополнения к строкам размещаются по столбцам.
Пример 1.14. Найти обратную матрицу к матрице 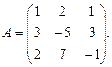
Решение. Вычисляем определитель и алгебраические дополнения (для удобства алгебраические дополнения элементов строк записываем по столбцам):

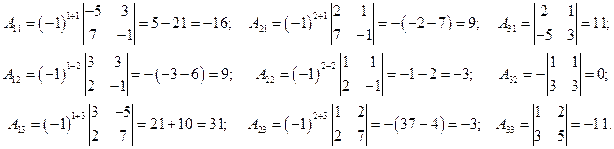
Таким образом 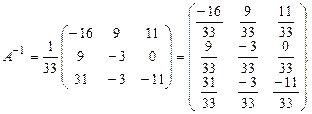
Проверим, верно ли нашли обратную матрицу.
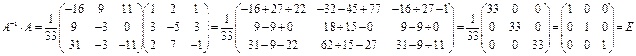
Обратная матрица найдена верно.
Есть и другой метод вычисления обратной матрицы. Справа к матрице А дописывают соответствующего порядка единичную матрицу и проводят элементарные преобразования так, чтобы на месте матрицы А получилась единичная матрица. Тогда на месте единичной матрицы будет обратная матрица А-1.
Пример 1.15. Найти обратную матрицу с помощью элементарных преобразований.
Решение.
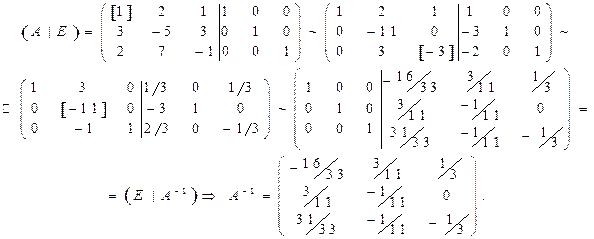
Проверка 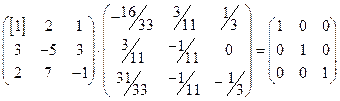 .
.
Для невырожденных матриц выполняются следующие свойства:
|
1. | 2. 
| 4. 
|
3. 
| 5. 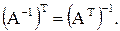
|
Дата: 2018-11-18, просмотров: 388.