Для планирования экономической деятельности или описания результатов используются упорядоченные наборы чисел, например, в платежной ведомости по столбцам выписываются: вычисленные суммы, удержанные профсоюзные взносы, выплаченные суммы; по строчкам — данные по каждому сотруднику. 

Аналогичная форма записи используется, если надо задать объемы выпуска продукции различных видов предприятиями одной отрасли и т.п. В итоге получается некоторая таблица чисел. Объекты такого рода хорошо изучены в математике и называются матрицами.

Определение 1.1. Матрицей называется прямоугольная таблица из m ´ n чисел, содержащая m строк и  n столбцов . Матрицу обозначают

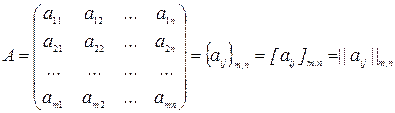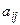, где  элементы матрицы; i — номер строки, j — номер столбца, в которых находится элемент  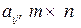—порядок матрицы.

Если 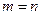, то матрица называется квадратной. Если 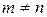, то матрица называется прямоугольной. Элементы  образуют главную диагональ (элементы главной диагонали) квадратной матрицы порядка n. Элементы 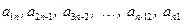 образуют побочную диагональ (элементы побочной диагонали) квадратной матрицы порядка n.

Определение 1.2. Матрица, которая имеет одну строку (столбец), называется матрицей-строкой (матрицей-столбцом) или вектором. Если все элементы матрицы равны нулю, то такая матрица называется нулевой (О). Квадратная матрица, у которой все элементы 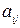 при 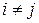 равны нулю, называется диагональной. Единичной матрицей называется квадратная матрица, у которой все элементы главной диагонали равны единицам, а остальные нули. Единичную матрицу обозначают Е или I.

Определение 1.3. Транспонированной матрицей к матрице А называют матрицу 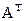, которая получается из А, когда меняются местами соответствующие строки и столбцы.

 Приведем примеры некоторых матриц:

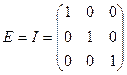— диагональная,   — единичная,

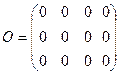— нулевая,                        .

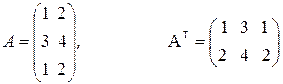— транспонированная к А матрица.

Действия над матрицами

Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичны операциям над числами, а некоторые свойственны только матрицам.

Определение 1.4. Две матрицы равны, если равны их порядки и соответствующие элементы.

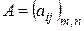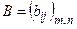Суммой матриц  и  называется матрица .

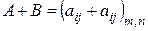Произведениемматрицы 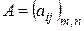 на число k называется матрица .

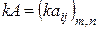Произведением матрицы 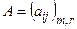 порядка  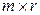на матрицу  порядка 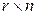 называется матрица  порядка 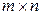, у которой элемент  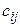равен скалярному произведению i — ой строки матрицы А на j – ый столбец матрицы В, т.е. .

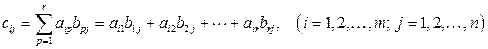Таким образом, произведение матриц определено, если количество столбцов первой матрицы равно количеству строк второй матрицы.

Возведение в степень. Целой положительной степенью 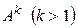 квадратной матрицы А называется произведение k матриц, равных, А. т.е.

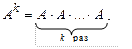
Операции сложения матриц, умножения матрицы на число и умножение матриц имеют следующие свойства:

1.   

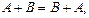
2.

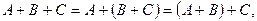
3.

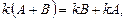
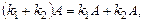
4.

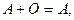
5. Существует (–A), такая, что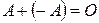

6.

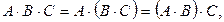
7.

8.

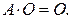
Замечания.

1. В общем случае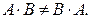

2. 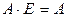 и .

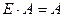Пример 1.1. Заданы матрицы А и В. Найти 2А–3В.

Решение.

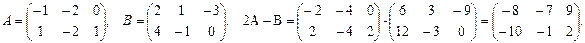Пример 1.2. Найти произведение матриц А и В, если

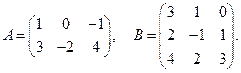
Решение.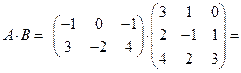

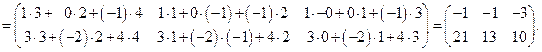Пример 1.3. Проверить выполнение равенства  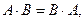если

Решение.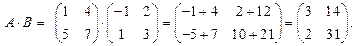

Пример 1.4. Проверить выполнение равенства .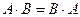

Решение.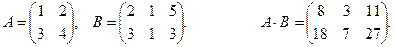

Матрица В имеет порядок 2×3, а А - 2×2. Поскольку число столбцов матрицы В не равно числу строк А, то перемножить матрицы нельзя. Следовательно, равенство не выполняется.

Пример 1.5. Найти 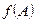, если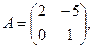  

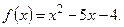
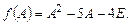
Решение.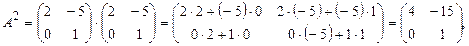  

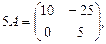
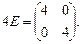Поэтому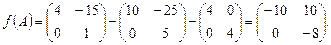

Элементарными преобразованиями матрицы называют следующие действия над ними:

1. Перестановка строк (столбцов).

2. Умножение строки (столбца) на число отличное от нуля.

3. Прибавление к элементам одной строки (столбца) элементов другой строки (столбца).

Приведем один пример использования матриц для описания и решения экономической задачи.

Пример 1.6. Пусть S₁, S₂ – два вида сырья, которые используются при изготовлении продуктов P₁,P₂, P₃.  Обозначим a_ij (i = 1,2; j = 1,2,3) – количество единиц сырья i-го вида, необходимого для выпуска единицы j-го продукта. Все числа a_ij образуют матрицу А, называемую технологической матрицей нормозатрат.

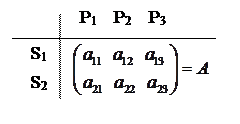
Предположим, что каждый их технологических продуктов P₁,P₂, P₃ является сырьем для производства продуктов П₁, П₂. Обозначим соответствующую технологическую матрицу нормозатрат В = (b_ij) (i = 1,2,3; j = 1,2).

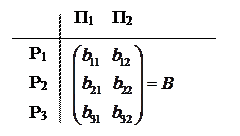
Здесь также b_ij – количество единиц продукции P_i, которое используется для производства единицы продукции П_j.

Найдем технологическую матрицу С нормозатрат исходных видов сырья S₁, S₂  на производство продукции П₁, П₂.

Решение. Так на производство b₁₁ единиц продукта P₁ расходуется a₁₁ b₁₁ сырья S₁, на производство b₂₁ единиц продукта P₁ используется a₁₂ b₂₁ сырья S₁, на производство b₃₁ единиц P₁ используется a₁₃ b₃₁ сырья S₁, то общее количество сырья S₁, необходимое для изготовления единицы продукции П₁,

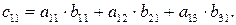
Рассуждая аналогично, получаем количество сырья S₁, необходимое для изготовления единицы продукции П₂.

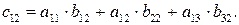
Количество сырья S₃ второго вида, которое используется для изготовления единиц продукции П₁ и П₂, найдем соответственно по формулам

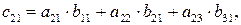
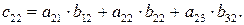
Таким образом, мы получили, что матрица С = А^.В и имеет вид

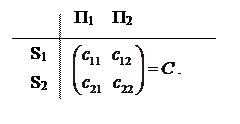
Здесь, как и для матриц А, В, с_ij (i = 1,2; j = 1,2) — количество сырья S_i, которое расходуется на производство единицы продукта П_j.

ОПРЕДЕЛИТЕЛИ