При решении размерных цепей данным методом составляющие размеры и замыкающий размер, который является функцией n-го количества составляющих, рассматриваются как величины случайные, какими они на самом деле и являются.

Сущность метода: при решении размерных цепей данным методом на составляющие размеры назначают допуски такой величины, при которых требуемое значение замыкающего размера обеспечивается не у всех, а лишь у определенного процента сборок, т.е. при данном методе не всегда выдерживается условие:

A_Dmin £ A_D £ A_Dmax..

И следовательно часть сборок пойдет в брак. Величиной допускаемого % брака задаются заранее. Наиболее часто эту величину принимают равной 0,027%.

Основные расчетные формулы для решения размерной цепи теоретико-вероятностным методом имеют вид:

1 Предельные значения замыкающего размера.

A_{Dmax (min)} = N_D + E_CD ± 0,5T_D.

2 Номинальные значения замыкающего размера.

.

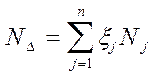3 Среднее отклонение замыкающего размера.

,

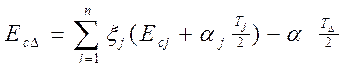где E_cj  -среднее значение составляющего размера;

a_j - коэффициент относительной асимметрии закона распределения случайной величины j-го составляющего размера;

T_j - допуск j -го составляющего размера;

a_D - коэффициент относительной асимметрии закона распределения случайной величины замыкающего размера;

T_D - допуск замыкающего размера.

При проектных расчетах размерных цепей можно пользоваться следующими значениями коэффициентов a:

- для размеров валов - a = +0,2;

- для размеров отверстий - a = - 0,2;

- для остальных a = 0;

- для замыкающего размера a_D = 0.

4 Допуск замыкающего размера

,

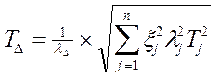где l_j - относительное средне-квадратическое отклонение j-го составляющего размера

l_D - относительное средне-квадратическое отклонение замыкающего размера.

При проектных расчетах можно пользоваться следующими значениями коэффициентов l:

- для составляющих размеров l = 0,4;

- для замыкающего размера l_D = 0,333.

Преимущества метода:

Возможность расширения допусков на изготовление составляющих размеров. При этом расширение допусков связано с величиной допускаемого процента брака на сборке и с количеством составляющих размеров в размерной цепи. Чем они больше, тем больше можно расширить допуски. Поэтому данный метод целесообразно применять когда число составляющих размеров больше 6.

Недостатки метода:

Некоторая сложность расчета и необходимость знать коэффициенты a и l.

Метод групповой взаимозаменяемости

Сущность метода:

При решении размерных цепей данным методом на составляющие размеры размерной цепи назначают расширенные допуски. Затем, перед сборкой детали делятся на размерные группы по степени фактической полномерности размеров. Сборку составляют из деталей одноименных сортировочных групп. Благодаря такой организации сборки удается повысить точность замыкающего размера.

Докажем это. При этом рассмотрим два случая (рис.32):

1 когда детали не делятся на размерные группы;

2 когда детали делятся на размерные группы.

Рассмотрим размерную цепь, в которой составляющими размерами являются размеры отверстия и вала. Замыкающим размером является натяг. Предположим, что допуск отверстия равен допуску вала Т_D = T_d = T. При данном методе расчет ведется на максимум и минимум.

Если детали не делятся на размерные группы, то

1 Допуск замыкающего размера равен:

T_i = i_max – i_min = Т_D + T_d = 2T.

Рисунок 32 – Схема к расчету размерных цепей методом групповой

Взаимозаменяемости

3 Среднее значение замыкающего размера (в нашем случае натяг) равно:

.

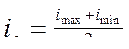4 Натяг в пределах каждой сборки изменяется от i_max до i_min:

.

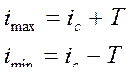Если детали поделить на размерные группы, то

1 Допуск замыкающего размера

.

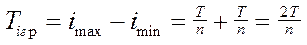Вывод: при равных допусках сопрягаемых деталей и при делении деталей на группы допуск замыкающего размера в группе уменьшается пропорционально количеству групп, по сравнению с допуском замыкающего размера до деления на группы. Т.е. точность сборки повышается пропорционально количеству групп.

2 Среднее значение замыкающего размера в группе:

.

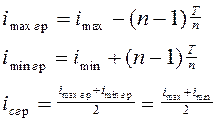Вывод: Среднее значение замыкающего размера в группе остается постоянным и равно среднему значению замыкающего размера до деления на группы. Натяг в пределах каждой группы изменяется в пределах:

.

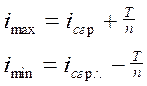Пример: определить значения зазоров в в соединении между отверстием в верхней головке шатуна и поршневым пальцем автомобильного двигателя, если размеры деталей:

отверстия в шатуне ;

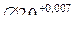палец .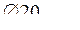

Детали перед сборкой делятся на четыре группы.

Если детали не делить на размерные группы, то

s_max = ES - ei = +7 - (-10) = +17 мкм

s_min = EI - es = -3 - 0 = -3 мкм

Допуск зазора:

T_s = s_max - s_min = +17 - (-3) =20 мкм

Средний зазор:

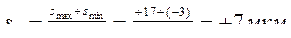
s_max(min) = s_с ± T/2 = 7 ± 10 мкм

Поделим детали на четыре группы по 2,5 мкм.

Тогда      s_{max гр} = +7 -(-2,5) = 9,5 мкм

s_{min гр} = +4,5 - 0 = 4,5 мкм

T_s = s_max - s_min = +9,5 - 4,5 = +5 мкм

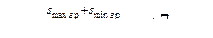
s_{max(min) гр} = s_гр ± T = 7 ± 2,5мкм

Метод групповой взаимозаменяемости широко применяется при сборке подшипников качения, при сборке деталей топливной аппаратуры, при сборке поршней с поршневыми пальцами, в поршневых компрессорах.

Преимущества метода:

возможность расширения допусков на изготовление составляющих размеров.

Недостатки метода:

необходимость 100% контроля деталей с целью отнесения их к той или иной сортировочной группе, необходимость маркировки деталей, необходимость раздельного хранения и транспортировки к месту сборки деталей каждой сортировочной группы. Наиболее существенным недостатком является возможность появления недоукомплектованных сборок, так как количество деталей в одноименных группах неодинаково.