Сущность метода заключается в том, что допуски составляющих размеров назначаются такими, при которых обеспечивается необходимая точность замыкающего размера в 100% сборок. При этом сама сборка ведется без подбора, регулировки, доработки. Таким образом, при данном методе всегда обеспечивается условие:

A_Dmin £ A_D £ A_Dmax

Метод предполагает:

1 что на сборку приходят все детали, имеющие предельные значения;

2 в каждой сборке составляющие размеры сочетаются таким образом, что замыкающий размер получает свои предельные значения.

Найдем основные расчетные формулы для решения размерной цепи данным методом. Расчет будем производить методом максимум - минимум.

Начнем с того, что запишем уравнение размерной цепи (рис.29).

А_D = А₁ - А₂ - А₃

Исходя из сущности метода максимум - минимум можно записать:

А_Dmax = А_1max - А_2min - А_3min

А_Dmin = А_1min - А_2max - А_3max

Вычтем из первого уравнения второе.

А_Dmax - А_Dmin = А_1max - А_1min + А_2max - А_2min + А_3max - А_3min

Т_D = Т₁ + Т₂ + Т₃

Таким образом допуск замыкающего размера равен сумме допусков составляющих размеров.

Т_D = .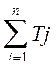

Полученное уравнение справедливо когда величина передаточного отношения по абсолютной величине равна 1 (çx_jç = 1), т.е. когда размеры параллельны друг другу. В общем случае уравнение 3 запишется следующим образом:

Т_D = .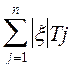

Пользуясь уравнением, исходя из заданного допуска замыкающего размера, рассчитывают допуски составляющих размеров. Это уравнение является условием правильности назначения допусков.

При увязке допусков замыкающего и составляющих размеров поступают так. Допусками для (n-1) размера задаются (стандартные допуски), а допуск n-го размера расчитывают. У этого размера допуск будет нестандартным.

Найдем уравнение, которое связывает отклонения замыкающего и составляющих размеров. В практике расчета размерных цепей пользуются не предельными отклонениями, а средним отклонением, которое определяется как полусумма верхнего и нижнего отклонения.

Eс  = .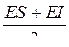

Зная Ес можно определить верхнее и нижнее откдлонения.

			Из рисунка видно, что ES = EC + 0,5 T EI = EC - 0,5T А max = N + EC + 0,5T Amin = N + EC - 0,5T AC = N + EC

Запишем уравнения

А_Dmax = А_1max - А_2min - А_3min

А_Dmin = А_1min - А_2max - А_3max

Сложим почленно эти уравнения и каждую сумму разделим пополам.

       (А_Dmax + А_Dmin)/2 = (А_1max + А_1min)/2 - (А_2max + А_2min)/2 - (А_3max - А_3min)/2

A_CD = A_C1 - A_C2 - A_C3

N_D + E_CD = N₁ + E_C1 - (N₂ + E_C2) - (N₃ + E_C3)

Вычтем из этого выражения номинальные размеры.

N_D = N₁ - N₂ - N₃

E_CD = E_C1 - E_C2 - E_C3

E_CD = (+1)E_C1 + (-1)E_C2 + (-1)E_C3

Таким образом мы получили

E_CD = .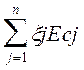

Пользуясь уравнением 5 осуществляют увязку средних отклонений замыкающего и составляющих размеров. При увязке отклонений принимают следующий характер расположения полей допусков составляющих размеров:

- для отверстия принимают поле допуска с основным отклонением Н (EI = 0);

- для валов - основное отклонение h (es = 0);

- для остальных - JS (±).

Проверку правильности назначения отклонений осуществляют пользуясь выражением 5.

Если условие 5 не выдерживается, то приходится на один из составляющих размеров назначать нестандартные отклонения. И значение среднего отклонения составляющего размера определяют пользуясь выражением 5.

Таким образом, основные расчетные формулы для решения размерных цепей методом полной взаимозаменяемости имеют вид:

Предельные значения замыкающего размера

А_Dmax = N_D + E_CD + 0,5T_D,

A_Dmin = N_D + E_CD - 0,5T_D.

Номинальное значение замыкающего размера

N_D = .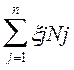

Среднее отклонение замыкающего размера

E_CD = .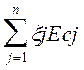

Допуск замыкающего размера

Т_D = .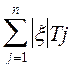

ПРЕИМУЩЕСТВА метода:

- обеспечение полной взаимозаменяемости; если все детали изготовлены в пределах их расчетных допусков, то брака на сборке быть не может (значение замыкающего размера находится в допустимых пределах);

- сборка ведется без доработки, регулировки, подбора;

- сборка легко нормируется по времени и не требует от сборщика высокой квалификации;

- облегчается процесс ремонта и эксплуатации изделия.

НЕДОСТАТКИ: при данном методе допуски на размеры получаются достаточно жесткими, поэтому данный метод целесообразно применять при сравнительно широком допуске на замыкающий размер и при небольшом числе составляющих размеров (n £ 6)

T_D = n*T_j ; T_j = T_D/n Þ c увеличением n допуски становятся жестче.