Числовой  последовательностью называется функция 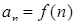, определенная на множестве натуральных чисел .

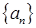 Последовательность называется возрастающей, если для любого номера n выполняется .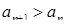

Последовательность называется убывающей, если для любого номера n выполняется .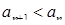

Возрастающие или убывающие последовательности называются монотонными.

Последовательность 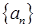 называется ограниченной сверху, если существует действительное число 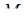такое, что для .

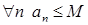Последовательность 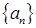 называется ограниченной снизу, если существует действительное число 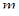такое, что для .

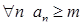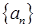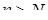Число a называется пределом последовательности , если для любого числа существует номер N такой, что для всех  выполняется неравенство .

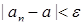В этом случае пишут .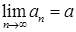

Свойства последовательностей имеющих предел:

Последовательность имеющая предел ограниченна

Последовательность может иметь только один предел.

Последовательность имеет предел тогда и только тогда, когда любая ее подпоследовательность имеет тот же предел.

Любая возрастающая (убывающая) и ограниченная сверху (снизу) числовая последовательность имеет предел.

Число 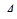 называется пределом функци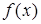и  при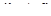  

если для .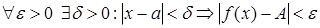

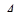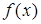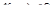
Число  называется пределом функции  при  если для .

Если определения не выполняются, то предел не существует. Если функция неограниченно возрастает при изменении аргумента, то пишут 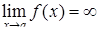 и называют бесконечно большой величиной

Функция 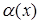называется бесконечно малой величиной при , если 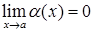, т.е. " e> 0 $ d> 0: .

Основные свойства бесконечно малых величин.

Если 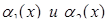 являются бесконечно малыми, то  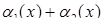также есть бесконечно малая величина.

Функция f ( x ) называется ограниченной при , если .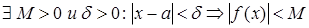

Произведение ограниченной при  функции на бесконечно малую есть бесконечно малая величина.

Произведение постоянной на бесконечно малую есть бесконечно малая величина.

Произведение двух бесконечно малых есть величина бесконечно малая.

Если 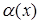является бесконечно малой величиной, то  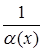является бесконечно большой величиной.

Если 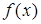 – бесконечно большая величина, то  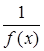– бесконечно малая величина.

Основные теоремы о пределах.

 Если функция имеет предел, то ее можно представить как сумму постоянной, равной ее пределу, и бесконечно малой величины.

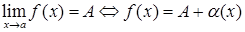, где 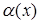– б.м.в. при .

Если существует предел функции, то он единственный.

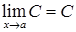. Предел константы равен самой константе.

.

.

.

.

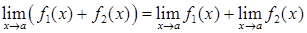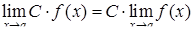Если в некоторой окрестности точки  выполняется 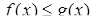, то .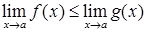

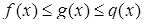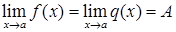Если в некоторой окрестности точки  выполняется  и , то .

Замечательные пределы. Непрерывность функций.

Первый замечательный предел .

Следствия из первого замечательного предела.

; ; ; ; .

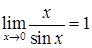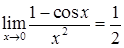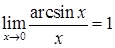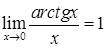 Второй замечательный предел.

Предел последовательности .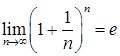

Для функции непрерывного аргумента "xÎR  или .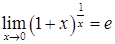

Следствия из второго замечательного предела.

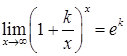 или .

Пусть a(x) и b(x) две бесконечно малые величины при x®a.

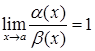 a(x) и b(x) называются эквивалентными бесконечно малыми. Обозначение a(x)~b(x) при x®a.

Если существует предел отношения двух бесконечно малых a(x) и b(x), то он равен пределу отношения соответствующих им эквивалентных бесконечно малых.

Таблица эквивалентных бесконечно малых величин при условии  

;                      ;

;            ;

;               ;

;                    .

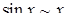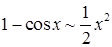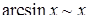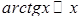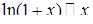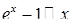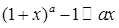Пусть функция определена на интервале [a; b] и x, x ₀Î[a; b].

Обозначим 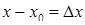, тогда 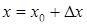, 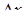называется приращением аргумента. Приращением функции соответствующим данному приращению аргумента назовем разность .

Функция называется непрерывной, если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е. .

Другое определение непрерывности функции: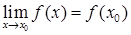

Функция непрерывная в каждой точке интервала (a;b) называется непрерывной на этом интервале.

Все элементарные функции непрерывны на своей области определения.

Точки разрыва функции.

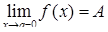Определяя понятие предела функции , подразумеваем, что  и 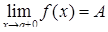. Такие пределы называются односторонними (левый и правый). Таким образом, функция непрерывна в точке 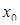, если выполняются условия: функция  определена в точке 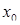 и

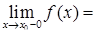
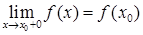. Если одно из этих условий нарушено, то функция имеет разрыв в указанной точке.

а) Если 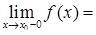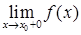, а функция неопределенна в точке 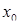, то такой разрыв называется устранимым. Его можно устранить, доопределив функцию.

б) Если существуют 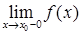 и 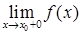, но они не равны между собой, то точка  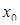называется точкой разрыва первого рода.

Все прочие точки разрыва называются точками разрыва второго рода.

Литература

1. Пискунов, Н. С. Дифференциальное и интегральное исчисления: учеб. пособие для втузов: [в 2 т.]. Т. 1 / Н. С. Пискунов. - Изд. стер. - М.: Интеграл-Пресс, 2009. - 544 с.: ил.

2. . Ефимов, Н. В. Краткий курс аналитической геометрии : учебник для вузов / Н. В. Ефимов . - Изд. 13-е, стер. - М. : ФИЗМАТЛИТ , 2005 . - 238 с.

3. Шипачев, В. С. Высшая математика : Базовый курс: учеб. пособие для вузов / В. С. Шипачев . - 8-е изд., перераб. и доп. - М. : Юрайт , 2011 . - 447 с.

4. Данко, П. Е. Высшая математика в упражнениях и задачах: в 2 ч. Ч. 1 / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. - 6-е изд. - М.: ОНИКС 21 век: Мир и Образование, 2003. - 416 с.

Содержание

1. Введение ……………………………………………3

2. Задания контрольных работ………………………..3

3. Разбор заданий контрольной работы № 1………..14

4. Разбор заданий контрольной работы № 2………..21

5. Разбор заданий контрольной работы № 3………..26

6. Справочный теоретический материал…………….31

7. Литература………………………………………….54