Тема 6. Предел последовательности. Предел функции, непрерывность функции.

Задача 1. а) Вычислить предел числовой последовательности

.

Решение. Числитель и знаменатель дроби неограниченно возрастают, поэтому дробь необходимо преобразовать. Сначала используем формулы сокращенного умножения

.

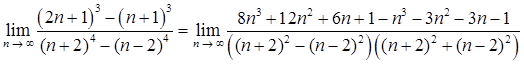
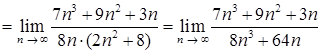Для того, чтобы избавиться от неопределенности 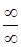 поделим числитель и знаменатель на старшую степень переменной, т.е. на 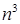. Получим, .

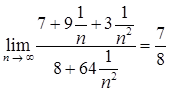 б) Вычислить предел числовой последовательности .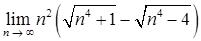

Решение. Для того, чтобы раскрыть неопределенность 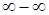 преобразуем общий член последовательности  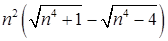умножив и поделив его на выражение, сопряженное выражению в скобках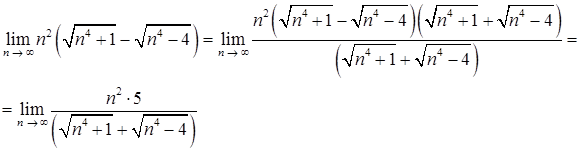   

Поделив числитель и знаменатель на старшую степень неизвестного, получим .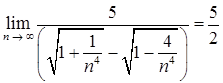

в) Вычислить предел числовой последовательности .

Решение. По определению число 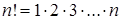. Преобразуем дробь и получим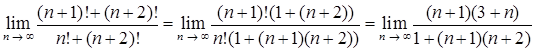

.

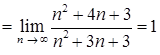Задача 2.

1) Вычислить предел функции .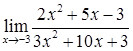 

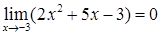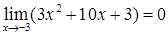Решение. Используя основные теоремы о пределах видим, что  и . Таким образом выражение  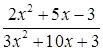представляет неопределенность  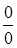при 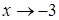. Чтобы раскрыть эту неопределенность числитель и знаменатель дроби разложим на множители, найдя корни многочленов. Уравнение  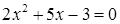имеет корни 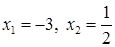. Уравнение  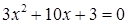имеет корни 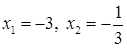. Тогда .

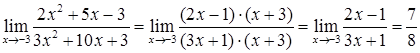2) Вычислить предел функции .

Решение. Так как числитель и знаменатель дроби неограниченно возрастают при неограниченном возрастании аргумента, то выражение 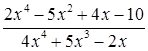 представляет неопределенность  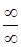. раскроем эту неопределенность поделив числитель и знаменатель дроби на старшую степень переменного т.е. на 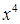. Получим  .

3) Вычислить предел функции .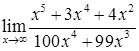

Решение. Также как в предыдущем случае, неопределенность 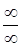 и раскрываем ее аналогично. .

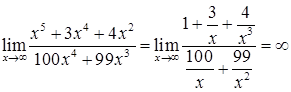4) Вычислить предел функции .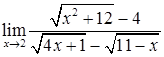

Решение. Выражение 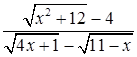 представляет неопределенность  при 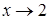.для того, чтобы раскрыть эту неопределенность преобразуем дробь умножив сначала числитель и знаменатель на выражение сопряженное числителю

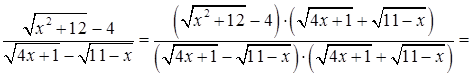
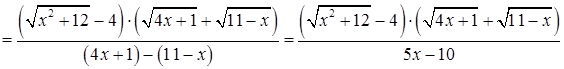. Затем аналогично умножим числитель и знаменатель дроби на выражение сопряженное числителю исходной дроби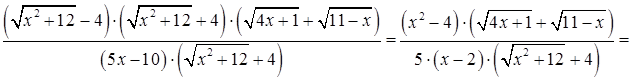

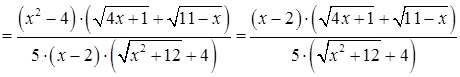. Выполнив преобразования, вычислим предел, используя основные теоремы о пределах .

 5) Вычислить предел функции .

Решение. Убедимся, что выражение 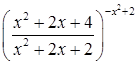 представляет неопределенность вида 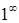. Действительно 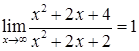, а 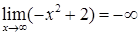. Преобразуем основание степени 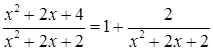, тогда вся степень может быть преобразована следующим образом 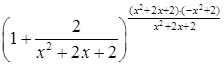. Продолжим вычисление предела, используя свойство непрерывности функции . .

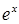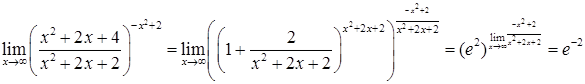5) Вычислить предел функции .

Решение. Воспользуемся таблицей эквивалентных бесконечно малых величин 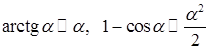 при 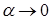. Тогда .

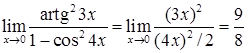Задача 3. Исследовать данную функцию на непрерывность и построить ее график  .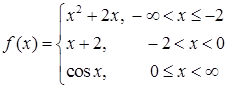

Решение. На интервалах 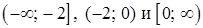 функция непрерывна, поэтому исследовать ее на непрерывность нужно в точках 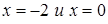. Вычислим значения функции и ее односторонние пределы в данных точках.

а) В точке 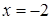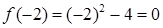, , 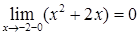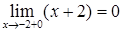. Односторонние пределы равны между собой и равны значению функции в данной точке, значит функция в точке 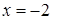непрерывна.

б) В точке 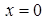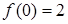, , 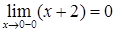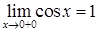. Односторонние пределы конечны, но не равны между собой, значит, функция в точке  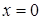имеет конечный разрыв (разрыв первого рода).