Тема 3. Основные понятия векторной алгебры.
Тема 4. Аналитическая геометрия в пространстве.
Тема 5. Аналитическая геометрия на плоскости.
Задача 1. Найти косинус угла между векторами 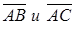 и площадь параллелограмма, построенного на этих векторах, если известны координаты точек
и площадь параллелограмма, построенного на этих векторах, если известны координаты точек 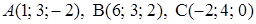 .
.
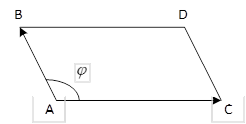
Решение. Найдем координаты векторов 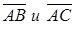 .
.
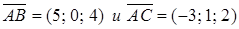 .
.
Угол между векторами найдем с помощью скалярного произведения векторов 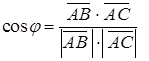 , где
, где 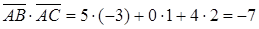 и
и 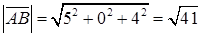 ,
, 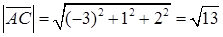 .
.
Тогда 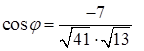 .
.
Площадь параллелограмма найдем с помощью модуля векторного произведения векторов 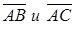 .
.
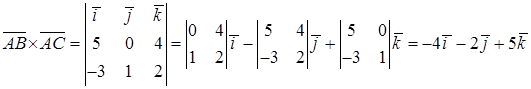
и  .
.
Задача 2. Даны координаты вершин пирамиды
 . Найти уравнение прямой
. Найти уравнение прямой  , уравнение плоскости
, уравнение плоскости 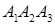 , уравнение высоты, опущенной из вершины
, уравнение высоты, опущенной из вершины 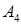 на грань
на грань 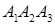 , вычислить объем пирамиды и расстояние от точки
, вычислить объем пирамиды и расстояние от точки 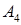 до плоскости
до плоскости  .
.
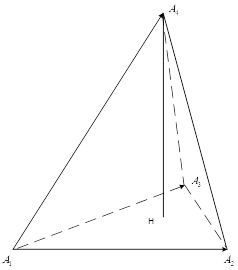
Решение. Найдем координаты векторов
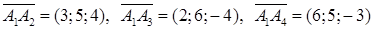 .
.
Напишем уравнение прямой 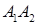 , проходящей через точку
, проходящей через точку 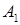 коллинеарно вектору
коллинеарно вектору 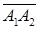 :
: 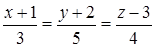 .
.
Для того, чтобы написать уравнение плоскости 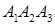 используем уравнение плоскости, проходящей через три заданные точки
используем уравнение плоскости, проходящей через три заданные точки  . Раскрывая определитель, получаем уравнение
. Раскрывая определитель, получаем уравнение
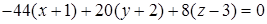 .
.
Упростим полученный результат, и находим уравнение плоскости 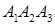 :
: 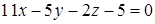 .
.
Нормальный вектор плоскости 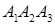
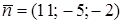 коллинеарен высоте пирамиды
коллинеарен высоте пирамиды 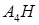 , а значит он является направляющим вектором прямой
, а значит он является направляющим вектором прямой 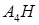 .
.
Таким образом, уравнение высоты  имеет вид
имеет вид
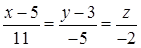 .
.
Объем пирамиды вычислим используя геометрический смысл смешанного произведения: 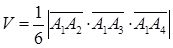 . Смешанное произведение вычислим как определитель третьего порядка составленный из координат векторов
. Смешанное произведение вычислим как определитель третьего порядка составленный из координат векторов 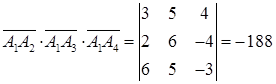 . Следовательно, объем пирамиды
. Следовательно, объем пирамиды 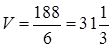 .
.
Расстояние от точки 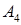 до плоскости
до плоскости  можно вычислить, если воспользоваться формулой
можно вычислить, если воспользоваться формулой 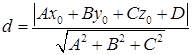 , где
, где 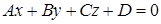 уравнение некоторой плоскости, а
уравнение некоторой плоскости, а 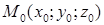 точка, не принадлежащая данной плоскости.
точка, не принадлежащая данной плоскости.
Тогда 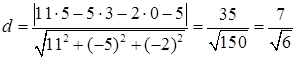 .
.
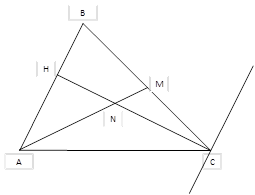
Задача 3. Даны координаты вершин треугольника
 .
.
Найти: а) уравнение высоты 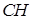 ; б) уравнение медианы
; б) уравнение медианы 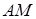 ; в) точку
; в) точку 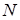 пересечения медианы
пересечения медианы 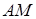 и высоты
и высоты 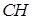 ; г) уравнение прямой, проходящей через точку
; г) уравнение прямой, проходящей через точку 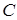 параллельно стороне
параллельно стороне 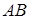 .
.
Решение.
а) Найдем координаты вектора 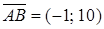 . Т.к. высота
. Т.к. высота 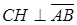 , то
, то  является нормальным вектором для прямой
является нормальным вектором для прямой  , таким образом уравнение высоты имеет вид
, таким образом уравнение высоты имеет вид 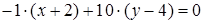 .
.
Упростим полученное уравнение и получим  .
.
б) Вычислим координаты точки 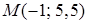 , как координаты середины отрезка
, как координаты середины отрезка 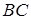 . Тогда уравнение прямой, проходящей через две заданные точки имеет вид
. Тогда уравнение прямой, проходящей через две заданные точки имеет вид 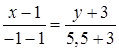 .
.
Выполним преобразование полученного уравнения
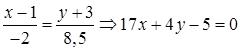 .
.
в) Вектор  коллинеарен искомой прямой, а значит служит для этой прямой направляющим вектором. Каноническое уравнение этой прямой имеет вид
коллинеарен искомой прямой, а значит служит для этой прямой направляющим вектором. Каноническое уравнение этой прямой имеет вид 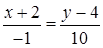 . Выполнив преобразования, получим
. Выполнив преобразования, получим 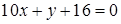 .
.
Задача 4. Составить уравнение линии, каждая точка 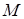 которой отстоит от точки
которой отстоит от точки  на расстоянии в три раза большем, чем от прямой
на расстоянии в три раза большем, чем от прямой 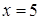 .
.
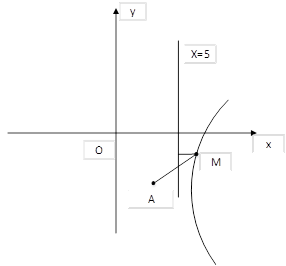 рис.1
рис.1
Решение. Пусть точка 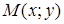 принадлежит искомой линии. Тогда расстояние
принадлежит искомой линии. Тогда расстояние 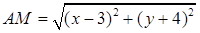 в три раза больше, чем расстояние
в три раза больше, чем расстояние 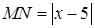 . Составим уравнение
. Составим уравнение  и преобразуем его.
и преобразуем его. 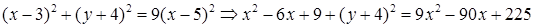
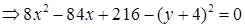 . Продолжим преобразования
. Продолжим преобразования 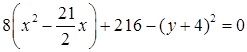 . Выделим полный квадрат по переменной
. Выделим полный квадрат по переменной 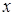 и получим
и получим  или
или 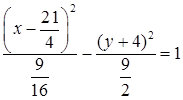 . Получили уравнение гиперболы, центр которой находится в точке с
. Получили уравнение гиперболы, центр которой находится в точке с  , а полуоси
, а полуоси 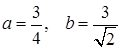 .
.
 рис.2
рис.2
Дата: 2018-11-18, просмотров: 396.