Задача 1. Найти: а) область определения функции 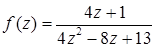 ;
;
б) значение функции  в точке
в точке 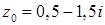 .
.
Решение.
а) Так как 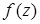 является дробно-рациональной функцией, то областью определения этой функции представляет собой множество всех комплексных чисел, исключая те, которые обращают знаменатель в ноль. Составим и решим уравнение
является дробно-рациональной функцией, то областью определения этой функции представляет собой множество всех комплексных чисел, исключая те, которые обращают знаменатель в ноль. Составим и решим уравнение 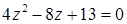 . Уравнение имеет комплексные корни, так как его дискриминант
. Уравнение имеет комплексные корни, так как его дискриминант 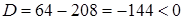 . Найдем корни:
. Найдем корни: 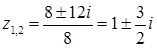 . Таким образом, областью определения функции
. Таким образом, областью определения функции 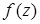 является множество всех комплексных чисел кроме
является множество всех комплексных чисел кроме  .
.
б) Найдем значение функции в заданной точке 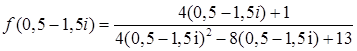 .
.
Выполним действия
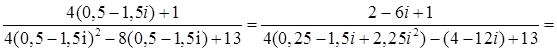
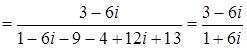 .
.
Для того, чтобы поделить два комплексных числа числитель и знаменатель дроби умножим на число сопряженной знаменателю получим  .
.
Таким образом, 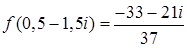 .
.
Задача 2. Найти все решения уравнения 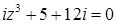 , используя формулу Муавра, ответ записать в тригонометрической форме.
, используя формулу Муавра, ответ записать в тригонометрической форме.
Решение.
Преобразуем уравнение так, чтобы выразить 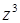 .
.
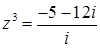 или
или 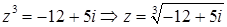 .
.
Найдем тригонометрическую форму комплексного числа:
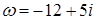 .
. 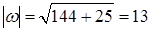 ,
,
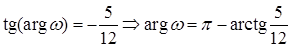 так как
так как 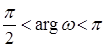 .
.
Тогда 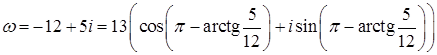 .
.
Используем формулу Муавра
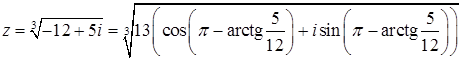
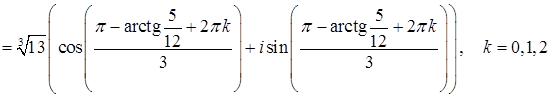 .
.
Уравнение 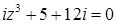 имеет 3 комплексных корня, получаемых при различных значениях
имеет 3 комплексных корня, получаемых при различных значениях 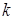 .
.
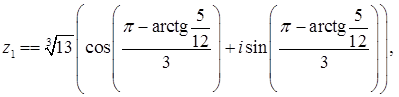
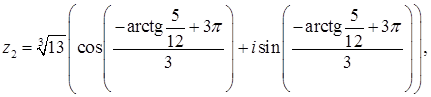
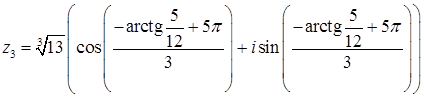 .
.
Задача 3. Решить матричное уравнение 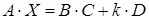 , где
, где
 ,
, 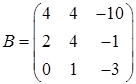 ,
, 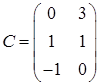 ,
, 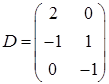 ,
, 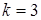
Решение:
Убедимся, что 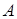 матрица не является вырожденной, то есть обладает обратной матрицей. Для этого вычислим её определитель:
матрица не является вырожденной, то есть обладает обратной матрицей. Для этого вычислим её определитель:
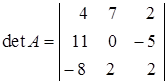 .
.
Разложим определитель, например, по элементам второго столбца:
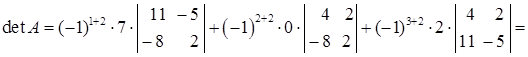
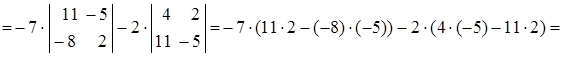 210.
210.
Определитель отличен от нуля, поэтому обратная матрица существует, и мы можем вычислить обратную матрицу по формуле:
 .
.
Вычислим алгебраические дополнения:
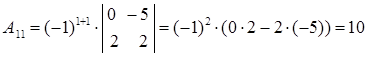
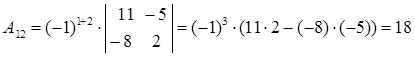
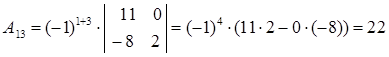
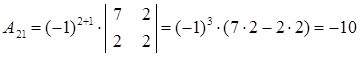
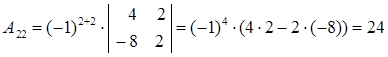
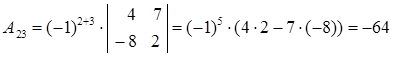

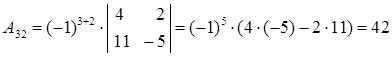
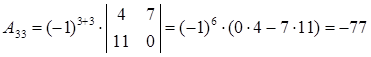
Таким образом, матрица, составленная из алгебраических дополнений, имеет вид:
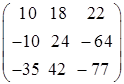 (
( 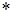 )
)
Транспонирование матрицы – такое преобразование этой матрицы, при котором ее строки становятся столбцами с теми же номерами. Транспонированная матрица к матрице ( 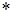 ) будет выглядеть так:
) будет выглядеть так:
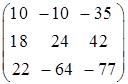 ,
,
тогда
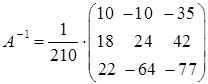 или
или 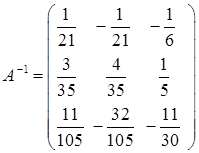 .
.
Таким образом, уравнение имеет единственное решение. Выполним преобразование левой части уравнения
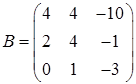 ,
, 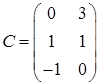 ,
, 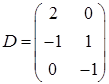 ,
, 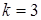
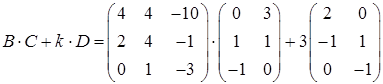 .
.
Обозначим произведение матриц 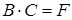 , где
, где  матрица размерности
матрица размерности 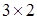 элементами
элементами  .
.
Получим  .
. 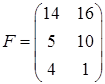 .
.
Матрица 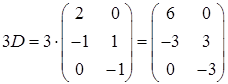
и  .
.
Исходное уравнение принимает вид
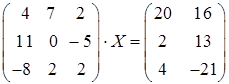 .
.
Умножим левую и правую части уравнения слева на 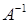 , получаем
, получаем 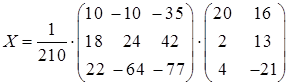 ,
,
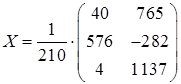 .
.
Задача 4. Решить систему уравнений, используя правило Крамера
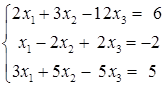
Решение:
Вычислим определитель матрицы, составленной из коэффициентов, стоящих при переменных в предложенной системе линейных уравнений:
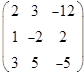
Его назовем главным определителем, 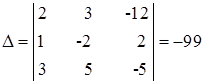 . Если главный определитель отличен от нуля, то система имеет единственное решение и найти его можно по правилу Крамера. Для этого заменим в матрице коэффициентов первый столбец на столбец свободных членов, и вычислим определитель такой матрицы:
. Если главный определитель отличен от нуля, то система имеет единственное решение и найти его можно по правилу Крамера. Для этого заменим в матрице коэффициентов первый столбец на столбец свободных членов, и вычислим определитель такой матрицы:
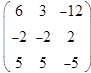
| 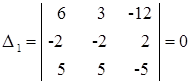
|
Аналогичным образом, получаем матрицы с замененными вторым и третьим столбцами соответственно, затем, вычислим определители этих матриц.
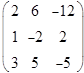
| 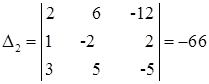
|

| 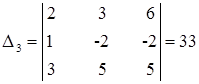
|
Решение системы можно найти таким образом:
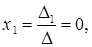
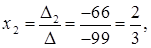
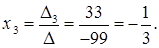
Задача 5. Доказать совместность системы и найти ее решение
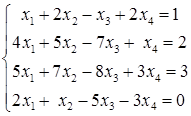
Решение:
Запишем расширенную матрицу системы
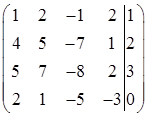
Вычтем из второй строки первую, предварительно умноженную на 4
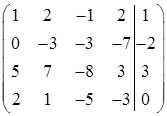
Вычтем из третьей строки первую, умноженную на 5
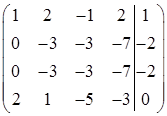
Наконец, вычтем из четвертой строки первую, умноженную на два

Затем вторую строку умножим на – 1 и прибавим ее к третьей и четвертой строкам
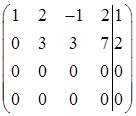 .
.
Ранг матрицы равен рангу расширенной матрицы и равен 2. Число свободных неизвестных в общем случае равно 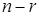 , где n – количество неизвестных системы, r – ранг матрицы системы. У нас число свободных неизвестных равно 4 – 2 = 2.
, где n – количество неизвестных системы, r – ранг матрицы системы. У нас число свободных неизвестных равно 4 – 2 = 2.
Новой расширенной матрице соответствует система
 .
.
Пусть 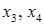 – свободные переменные, принимающие любые действительные значения. Все остальные неизвестные выразим через них. Из второго уравнения системы выразим
– свободные переменные, принимающие любые действительные значения. Все остальные неизвестные выразим через них. Из второго уравнения системы выразим 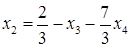 .
.
Подставляя найденное выражение для 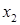 в первое уравнение, получаем
в первое уравнение, получаем 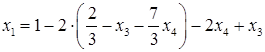
 .
.
Таким образом, общее решение системы имеет вид 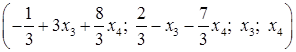 (
( 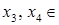 R).
R).
Дата: 2018-11-18, просмотров: 348.