Аннотация: Рассмотрена методика выбора наименее рискованного инвестиционного проекта на основе вероятностных критериев.
Ключевые слова: основной капитал, затраты, реальное значение, финансовые рынки, теория игр, значение, сценарий, максимум, прибыль, критерий Вальда, ПО, матрица, инвестиционный проект, разность, индекс доходности, доходность, величина риска, вероятность
Цель лекции: освоить методику расчета вероятностных критериев риска и выбора наименее рискованного варианта инвестирования.
Практика хозяйственной деятельности нередко вынуждает принимать решения, связанные с выбором оптимального варианта инвестирования в условиях риска и неопределенности. Инвестор, имеющий некоторую сумму, выбирает между несколькими инвестиционными проектами. Предприятие может стоять перед выбором направления инвестирования в основной, человеческий или природный капитал. Если направление инвестирования выбрано, возникают другие вопросы: так, если речь идет об инвестициях в основной капитал, то возникает проблема выбора конкретной техники и технологии. Инвестиции в человеческий капитал могут быть выражены либо в улучшении системы социального обеспечения работников предприятия, либо в их дополнительном образовании. Инвестиции в природный капитал могут быть направлены на строительство очистных сооружений или на приобретение нового оборудования, которое позволит снизить ресурсоемкость производства, и т.п. При этом неопределенность существует практически всегда. Параметры нового оборудования, уровень готовности персонала к работе на нем, затраты на монтаж можно прогнозировать, но зачастую реальные значения существенно отличаются от прогнозных. Оценка эффективности инвестиций в природный и человеческий капитал вообще является достаточно сложной экономической проблемой из-за трудности денежной оценки результата таких инвестиций. Кроме того, инвестор, как правило, не может прогнозировать макроэкономические изменения: структурные сдвиги, смену экономических циклов, процессы на международном валютно-финансовом рынке. Таким образом, выбор оптимального варианта инвестирования — это нахождение проекта, удовлетворяющего инвестора с точки зрения доходности и риска.
Существенную помощь в решении подобных задач оказывают экономико-математические методы, а именно - использование теории игр и статистических решений. Методы теории игр позволяют глубже разобраться в ситуации, оценить каждое решение с разных точек зрения. В конечном итоге решающее значение имеет позиция инвестора относительно цели реализации проекта: либо он рассчитывает на оптимистический сценарий и хочет извлечь максимум выгоды (но в случае реализации негативных прогнозов он понесет существенные убытки), либо он хочет получить относительно небольшую, но гарантированную прибыль.
В ситуации выбора оптимального варианта инвестирования целесообразно рассчитать несколько критериев: критерий Вальда, критерий Сэвиджа, критерий Гурвица, критерий Байеса, критерий Лапласа.
Предположим, имеется 4 варианта инвестирования — проекты А, Б, В, Г. По каждому проекту возможны 4 сценария развития ситуации — оптимистический, консервативный, пессимистический и смешанный. Для расчета вероятностных критериев риска нужно составить матрицу доходности и матрицу рисков. Элементами матрицы доходности являются индексы доходности (ИД). Строки матрицы доходности обозначают варианты инвестирования, а столбцы – сценарии развития ситуации (таблица 17.1).
| Таблица 17.1. Матрица доходности | ||||
| Оптимистич. сценарий | Консервативый сценарий | Пессимистич. сценарий | Смешанный сценарий | |
| Проект А | 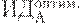
| 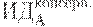
| 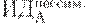
| 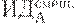
|
| Проект Б | 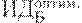
| 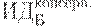
| 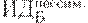
| 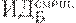
|
| Проект В | 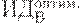
| 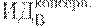
| 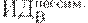
| 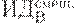
|
| Проект Г | 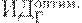
| 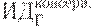
| 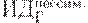
| 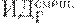
|
Матрица рисков имеет такую же структуру, как и матрица доходности (в строках – инвестиционные проекты, в столбцах – сценарии). Элементом матрицы рисков является разность между максимально возможным индексом доходности по данному сценарию и индексом доходности данного проекта по этому же сценарию (таблица 17.2).
| Таблица 17.2. Матрица рисков | ||||
| Оптимистич. сценарий | Консервативный сценарий | Пессимистич. сценарий | Смешанный сценарий | |
| Проект А | 
| 
| 
| 
|
| Проект Б | 
| 
| 
| 
|
| Проект В | 
| 
| 
| 
|
| Проект Г | 
| 
| 
| 
|
Критерий Вальда олицетворяет позицию "крайнего пессимизма", позволяя определить, какой проект даст наибольший доход при реализации пессимистического сценария:
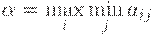
где 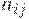 – элементы матрицы доходности.
– элементы матрицы доходности.
Критерий Сэвиджа также является критерием "крайнего пессимизма", но этот критерий советует при выборе оптимального решения ориентироваться не на доходность, а на риск. Использование критерия Сэвиджа оправдано в том случае, если инвестор хочет в любом случае избежать большого риска и готов ради этого упустить некоторую выгоду. Оптимальным считается тот инвестиционный проект, для которого величина риска при реализации пессимистического сценария минимальна:
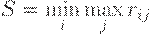
где 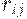 – элементы матрицы рисков.
– элементы матрицы рисков.
Критерий Гурвица рекомендует не рассматривать ситуацию ни с позиции "крайнего пессимизма", ни "крайнего оптимизма", то есть советует не рассчитывать ни на наилучшее, ни на наихудшее развитие событий. При расчете критерия Гурвица используется так называемый "коэффициент пессимизма" 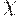 , значения которого находятся в интервале между нулем и единицей:
, значения которого находятся в интервале между нулем и единицей:
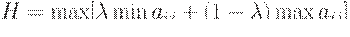
При 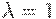 критерий Гурвица превращается в критерий Вальда, то есть в критерий "крайнего пессимизма". При
критерий Гурвица превращается в критерий Вальда, то есть в критерий "крайнего пессимизма". При  – в критерий "крайнего оптимизма", рекомендующий выбирать инвестиционный проект, дающий наибольший доход при реализации оптимистического сценария. Коэффициент пессимизма ? выбирается исходя из склонности инвестора к риску – чем меньше эта склонность, тем ближе к единице значение
– в критерий "крайнего оптимизма", рекомендующий выбирать инвестиционный проект, дающий наибольший доход при реализации оптимистического сценария. Коэффициент пессимизма ? выбирается исходя из склонности инвестора к риску – чем меньше эта склонность, тем ближе к единице значение 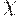 .
.
Критерий Байеса рекомендует выбирать тот инвестиционный проект, для которого математическое ожидание индекса доходности максимально:
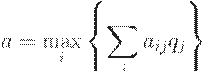
где 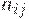 – элементы матрицы доходности;
– элементы матрицы доходности;
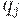
– вероятности наступления сценариев.
Критерий Лапласа отличается от критерия Байеса тем, что вероятности наступления сценариев принимаются равными.
Пример. Дана матрица доходности (таблица 17.3). Составить матрицу рисков и рассчитать критерии Вальда, Сэвиджа, Гурвица, Байеса, Лапласа. Коэффициент пессимизма равен 0,6. Вероятность наступления оптимистического сценария – 0,2, пессимистического – 0,2, смешанного – 0,1, консервативного – 0,5.
| Таблица 17.3. Матрица доходности | ||||
| Оптимистич. сценарий | Консервативный сценарий | Пессимистич. сценарий | Смешанный сценарий | |
| Проект А | 2,03 | 1,03 | -0,3 | 1,01 |
| Проект Б | 2,04 | 1,04 | -0,4 | 1,02 |
| Проект В | 2,05 | 1,05 | -0,5 | 1,15 |
| Проект Г | 2,06 | 1,06 | -0,6 | 1,32 |
Решение.
1. Определим максимальное значение по каждому столбцу матрицы доходности. Получим 2,06 для оптимистического сценария, 1,06 – для консервативного, -0,3 – для пессимистического и 1,32 для смешанного. Далее вычитаем из максимального по столбцу значения каждый элемент этого столбца. Например, определим риск по проекту А для оптимистического сценария:
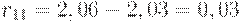
Аналогично определяем каждый элемент матрицы рисков и сводим полученные значения в таблицу 13.4 .
| Таблица 17.4. Матрица рисков | ||||
| Оптимистич. сценарий | Консервативный сценарий | Пессимистич. сценарий | Смешанный сценарий | |
| Проект А | 0,03 | 0,03 | 0,00 | 0,31 |
| Проект Б | 0,02 | 0,02 | 0,10 | 0,30 |
| Проект В | 0,01 | 0,01 | 0,20 | 0,17 |
| Проект Г | 0,00 | 0,00 | 0,30 | 0,00 |
Тема 2 Лекции 17
Продолжение
Чтобы определить критерий Вальда, нужно выбрать в матрице доходности проект, который даст наибольшую доходность при реализации пессимистического сценария:
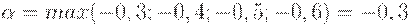
Оптимальным по критерию Вальда является проект А.
Для определения критерия Сэвиджа нужно выбрать в матрице рисков проект, для которого в случае реализации пессимистического сценария риск будет минимальным:
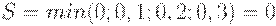
Оптимальным по критерию Сэвиджа является проект А.
Рассчитаем критерий Гурвица:
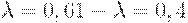
В каждой строке матрицы доходности минимальная доходность соответствует пессимистическому сценарию, а максимальная – оптимистическому.
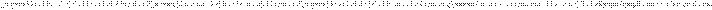
Оптимальным по критерию Гурвица является проект А.
Чтобы рассчитать критерий Байеса, нужно составить новую матрицу, умножив каждый элемент матрицы доходности на вероятность наступления соответствующего сценария (таблица 17.5, таблица 17.6):
| Таблица 17.5. Составление матрицы для расчета критерия Байеса | ||||
| Оптимистич. сценарий | Консервативный сценарий | Пессимистич. сценарий | Смешанный сценарий | |
| Проект А | 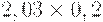
| 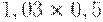
| 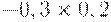
| 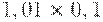
|
| Проект Б | 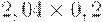
| 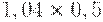
| 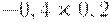
| 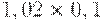
|
| Проект В | 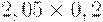
| 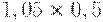
| 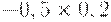
| 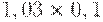
|
| Проект Г | 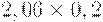
| 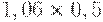
| 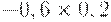
| 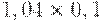
|
Рассчитав значения элементов, получим:
| Таблица 17.6. Матрица для расчета критерия Байеса | ||||
| Оптимистич. сценарий | Консервативный сценарий | Пессимистич. сценарий | Смешанный сценарий | |
| Проект А | 0,41 | 0,52 | -0,06 | 0,10 |
| Проект Б | 0,41 | 0,52 | -0,08 | 0,10 |
| Проект В | 0,41 | 0,53 | -0,10 | 0,12 |
| Проект Г | 0,41 | 0,53 | -0,12 | 0,13 |
Определяем сумму по строкам матрицы.
Проект А:
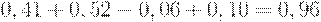
Проект Б:
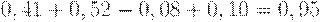
Проект В:
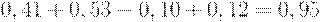
Проект Г:
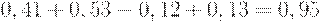
Критерий Байеса:
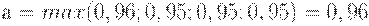
Оптимальным по критерию Байеса является проект А.
Для расчета критерия Лапласа также нужно составить дополнительную матрицу. Принцип ее составления остается таким же, как при расчете критерия Байеса, но вероятности наступления сценария принимаются равными, то есть по 0,25 (таблица 17.7, таблица 17.8).
| Таблица 17.7. Составление матрицы для расчета критерия Лапласа | ||||
| Оптимистич. сценарий | Консервативный сценарий | Пессимистич. сценарий | Смешанный сценарий | |
| Проект А | 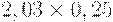
| 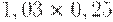
| 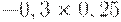
| 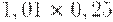
|
| Проект Б | 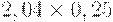
| 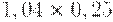
| 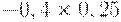
| 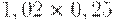
|
| Проект В | 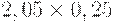
| 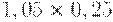
| 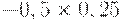
| 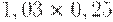
|
| Проект Г | 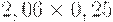
| 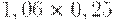
| 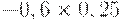
| 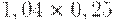
|
Рассчитав значения элементов, получим:
| Таблица 17.8. Матрица для расчета критерия Лапласа | ||||
| Оптимистич. сценарий | Консервативный сценарий | Пессимистич. сценарий | Смешанный сценарий | |
| Проект А | 0,51 | 0,26 | -0,08 | 0,25 |
| Проект Б | 0,51 | 0,26 | -0,10 | 0,26 |
| Проект В | 0,51 | 0,26 | -0,13 | 0,29 |
| Проект Г | 0,52 | 0,27 | -0,15 | 0,33 |
Далее определяем суммы по строкам матрицы.
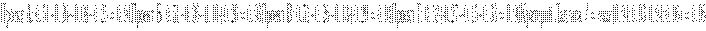
Оптимальным по критерию Лапласа является проект Г.
Краткие итоги:
· Хозяйственная деятельность связана с постоянным выбором вариантов инвестирования.
· Для выбора оптимального варианта инвестирования рассчитываются критерии Вальда, Сэвиджа, Гурвица, Байеса и Лапласа.
· Для расчета критериев необходимо составление матрицы доходности и матрицы рисков.
· Критерии Вальда и Сэвиджа олицетворяют позицию "крайнего пессимизма", но критерий Вальда ориентируется на доходность, а критерий Сэвиджа — на риск.
· Для расчета критерия Гурвица используется коэффициент пессимизма.
· Критерии Байеса и Лапласа указывают на тот проект, для которого математическое ожидание доходности максимально.
Упражнения:
1. Охарактеризуйте проблему принятия инвестиционного решения в условиях неопределенности.
2. Перечислите основные критерии выбора оптимального решения в условиях неопределенности.
3. Приведите формулы для расчета критериев Вальда, Сэвиджа, Гурвица, Байеса, Лапласа.
4. Дана матрица доходности. Составить матрицу рисков:
| вариант 1 | ||||
| Оптимистич. сценарий | Консервативный сценарий | Пессимистич. сценарий | Смешанный сценарий | |
| Проект А | 2,9 | 2 | 1 | 2 |
| Проект Б | 3,8 | 3 | 2 | 2,3 |
| Проект В | 4,6 | 4 | 3 | 2,7 |
| Проект Г | 3,1 | 3,1 | 0,5 | 2,9 |
| вариант 2 | ||||
| Оптимистич. сценарий | Консервативный сценарий | Пессимистич. сценарий | Смешанный сценарий | |
| Проект А | 1,9 | 1 | 1 | 1 |
| Проект Б | 1,8 | 1 | 1 | 1,1 |
| Проект В | 4,6 | 4 | 1 | 1,7 |
| Проект Г | 1,1 | 1,1 | 0,5 | 1,9 |
5. Рассчитать критерии Вальда, Сэвиджа, Гурвица, Байеса, Лапласа, используя матрицы доходности и рисков из предыдущего задания (упраженение 4).
Темы для зачетов, экзаменов, курсовых работ, рефератов:
1. Проблема выбора оптимального варианта инвестирования в современной экономике.
2. Экономико-математические методы оценки риска инвестиционного проекта.
КЭШ Временный
Дата: 2018-11-18, просмотров: 865.