Корреляционно-регрессионный анализ — классический метод стохастического моделирования хозяйственной деятельности. Он изучает взаимосвязи показателей хозяйственной деятельности, когда зависимость между ними не является строго функциональной и искажена влиянием посторонних, случайных факторов. При проведении корреляционно-регрессионного анализа строят различные корреляционные и регрессионные модели хозяйственной деятельности. В этих моделях выделяют факторные и результативные показатели (признаки). В зависимости от количества исследуемых показателей различают парные и многофакторные модели корреляционно-регрессионного анализа.

Основной задачей корреляционно-регрессионного анализа является выяснение формы и тесноты связи между результативным и факторным показателями. Под формой связи понимают тип аналитической формулы, выражающей зависимость результативного показателя от изменений факторного. Различают связь прямую, когда с ростом (снижением) значений факторного показателя наблюдается тенденция к росту (снижению) значений результативного показателя. В противном случав между показателями существует обратная связь. Форма связи может быть прямолинейной (ей соответствует уравнение прямой линии), когда наблюдается тенденция равномерного возрастания или убывания результативного показателя, в противном случае форма связи называется криволинейной (ей соответствует уравнение параболы, гиперболы и др.).

ОСНОВНЫЕ МОДЕЛИ КОРРЕЛЯЦИОННОГО АНАЛИЗА. Такими моделями являются: коэффициент парной корреляции, коэффициент частной корреляции, коэффициент множественной корреляции, коэффициент детерминации.

Значение коэффициента парной корреляции изменяется в пределах от -1 до +1. Знак «+» означает наличие прямой связи между показателями. Знак «-» — наличие обратной связи. Значение коэффициента от 0 до 1 характеризует степень приближения корреляционной зависимости между показателями и к функциональной. При р = 1 между показателями существует функциональная связь. При р = 0 линейная связь отсутствует. В целях упрощения расчетов на практике применяются и другие формулы коэффициента парной корреляции, представляющие собой некоторые преобразования исходной формулы.

Часто в анализе хозяйственной деятельности при изучении связи между показателями х и у требуется исключить воздействие третьего показателя z, выступающего как общий фактор изменения анализируемых показателей. Для этого используется коэффициент частной корреляции (rx,y,z), свойства которого совпадают со свойствами коэффициента парной корреляции

Коэффициент множественной корреляции (R) характеризует тесноту связи между результативным показателем и набором факторных показателей.

Коэффициент множественной корреляции принимает только положительные значения в пределах от 0 до 1. Чем ближе значение коэффициента к 1, тем больше теснота связи. И, наоборот, чем ближе к 0, тем зависимость меньше. При значении R < 0,3 говорят о малой зависимости между величинами. При значении 0,3 < R < 0,6 говорят о средней тесноте связи. При R > 0,6 говорят о наличии существенной связи.

Квадрат коэффициента множественной корреляции называется коэффициентом детерминации (D): D = R2. Коэффициент детерминации показывает, какая доля вариации результативного показателя связана с вариацией факторных показателей. В основе расчета коэффициента детерминации и коэффициента множественной корреляции лежит правило сложения дисперсий, согласно которому общая дисперсия (σ2) равна сумме межгрупповой дисперсии (δ2) и средней из групповых дисперсий σi2)

35. Методы анализа количественного влияния факторов на результативный показатель при различных видах взаимозависимостей

Метод цепных подстановок используется для исчисления влияния отдельных факторов на соответствующий совокупный показатель. Данный способ анализа используется лишь тогда, когда зависимость между изучаемыми явлениями имеет строго функциональный характер, когда она представляется в виде прямой или обратной пропорциональной зависимости. В этих случаях анализируемый совокупный показатель как функция нескольких переменных должен быть изображен в виде алгебраической суммы, произведения или частного от деления одних показателей на другие.

При расчетах необходимо придерживаться следующих правил:

сначала учитывается влияние количественных, а затем качественных факторов;

в первую очередь изменяется фактор первого уровня, затем второго, третьего и т.д.

В общем виде имеем следующую систему расчетов по методу цепных подстановок:

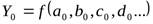— базисное значение обобщающего показателя;

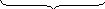факторы

y₀ = f(a₁b₀c₀d₀…) — промежуточное значение;

у₀ = f(a₁b₁c₀d₀...) — промежуточное значение;

у₀ = f(a₁b_lc_]d₀...) — промежуточное значение;

………………………………

у₀= f(a_lb_]c_ld_l...) — фактическое значение.

Общее абсолютное отклонение обобщающего показателя определяется по формуле

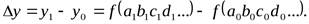
Общее отклонение обобщающего показателя раскладывается на факторы:

за счет изменения фактора а

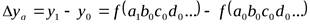
за счет изменения фактора b

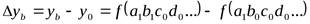
и т.д.

Метод цепных подстановок имеет недостатки, о которых следует знать при его применении. Во-первых, результаты расчетов зависят от последовательности замены факторов; во-вторых, активная роль в изменении обобщающего показателя необоснованно часто приписывается влиянию изменения качественного фактора.

Индексный метод основан на сопоставлении фактического уровня изучаемого объекта в отчетном периоде к его уровню в базисном периоде. Вместо значения в базисном периоде могут использоваться плановые величины.

Индексный метод используется для расчета влияния факторов в мультипликативных и кратных моделях.

Если обобщающий экономический показатель представляет собой произведение количественного (объемного) и качественного показателей-факторов, то при определении влияния количественного фактора качественный показатель фиксируется на базисном уровне, а при определении влияния качественного фактора количественный показатель фиксируется на уровне отчетного периода.

Метод абсолютных разниц. Применяется для расчета влияния факторов на результативный показатель в мультипликативных моделях и комбинированных моделях типа:

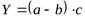и

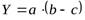
В соответствии с методом абсолютных разниц необходимо рассчитать абсолютный прирост каждого фактора. Затем величина влияния того или иного фактора определяется умножением его прироста на плановую величину факторов, находящихся в модели справа от него, и на фактическую величину факторов, находящихся слева.

Например, алгоритм расчета для мультипликативной модели типа 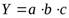имеет вид:

;

;

;

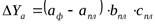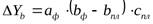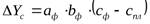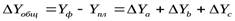
Метод относительных разниц. Используется в мультипликативных и комбинированных моделях. Сначала следует рассчитать относительный прирост каждого фактора. Далее величина влияния фактора на результативный показатель определяется умножением его относительного прироста на плановую величину результативного показателя.

Так, для мультипликативной модели типа 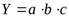относительные отклонения факторных показателей имеют вид:

; ; ;

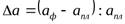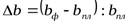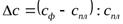Отклонение результативного показателя за счет влияния каждого фактора рассчитывается по формулам:

; ; ;

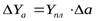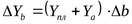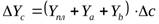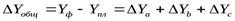
Метод дифференциального исчисления. Основан на формуле полного дифференциала. Для функции от двух переменных 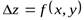имеем полное приращение функции :

;

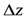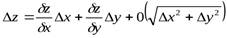где 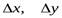- факторные приращения соответствующих переменных;

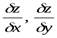- частные производные;

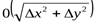- бесконечно малая величина более высокого порядка, чем 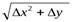. Эта величина в расчетах отбрасывается (ее часто обозначают ε.

Таким образом, влияние фактора х на обобщающий показатель определяется по формуле:

,

.

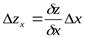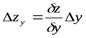Общее приращение результирующего показателя разлагается на слагаемые, где значение каждого из них определяется как произведение соответствующей производной на приращение фактора, по которому исчислена данная производная.

Интегральный метод факторного анализа. Он основан на суммировании приращения функции, определенной как частная производная, умноженная на приращение аргумента на бесконечно малых промежутках.

При этом должны выполняться некоторые условия:

подынтегральная функция должна быть непрерывной и дифференцируемой;

скорость изменения факторов должна быть постоянной величиной, т.е. dx=const/

В основе интегрального метода лежит интеграл Эйлера-Лагранжа, устанавливающий связь между приращением функции и приращением факторных признаков.

Для функции 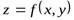имеем следующие формулы расчета факторных влияний:

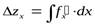- влияние фактора х;

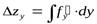- влияние фактора y.