Схема регулятора приведена на рис. 12, ниже приведены расчеты его емкостных и резистивных элементов. ПФ корректирующего звена:
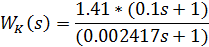
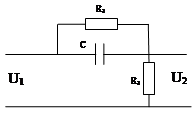
Рис. 12
Передаточная функция аналогового регулятора рассчитывается:
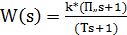; 𝜏>T;
;
;
.
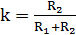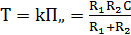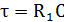В нашем случае:
𝜏 = Т3 = 0.1 с
Т = Т2 = 0.002417с
Зададим С = 0,1*10-6Ф. Найдем сопротивление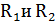 
.
; 
; 
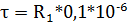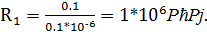
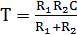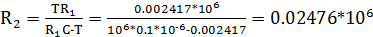Ом
.
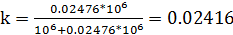Найдем численное значение магнитного усилителя:
; 
.
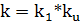Полученные значения:
;
;
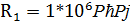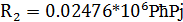С = 0,1*10-6Ф.
Записываем ПФ с учетом найденного значения коэффициента:
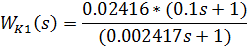
Коррекция на основе активных фильтров (операционных усилителей)
Регуляторы предназначены для формирования законов управления и часто реализуется на операционных усилителях.
Схема регулятора на ОУ приведена на рис. 13; ниже проведем расчет его емкостных элементов.
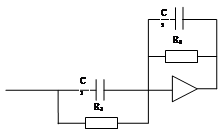
Рис. 13
;
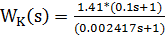Передаточная функция операционного усилителя рассчитывается:
;
.
.
.
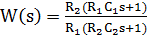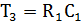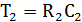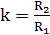Зададимся: 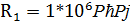. Найдем емкости С1 и С2 и сопротивление R2.
При этом:
𝜏 = Т3 = 0.1 с
Т = Т2 = 0.002417с
Находим значения емкостей и сопротивлений:
; 
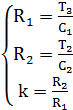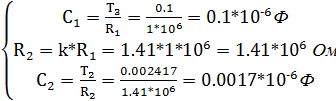
Получаем следующие значения:
;
;
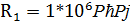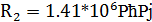С1 = 0.1*10-6Ф.
С2 = 0.0017*10-6Ф.
Записываем ПФ с учетом найденных значений:
;
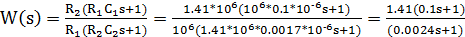Реализация цифрового регулятора
Цифровой регулятор может быть получен из передаточной функции корректирующего устройства путем перевода ее в дискретную форму с помощью аппроксимации тастина и последующей записи разностного уравнения.
На рис. 14 изображена общая структурная схема цифрового регулятора, принцип действия которого следующий: сигнал, поступающий в АЦП (аналогово-цифровой преобразователь), преобразуется из аналоговой формы в цифровую путем квантования непрерывной величины по времени, затем сигнал поступает в D(z) (цифровая вычислительная машина), где производятся вычисления согласно разностному уравнению, после чего сигнал поступает в ЦАП (цифро-аналоговый преобразователь), где и преобразуется из цифровой в аналоговую форму.
 |
Рис. 14
Чтобы найти значение периода дискретности, воспользуемся следующим неравенством:
; 
; 
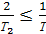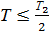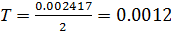с
Период дискретности равен ТS = 0.0012 с
Данную операцию осуществим с помощью MATLAB. Заносим полученную ПФ WK в MATLAB в zpk-форме:
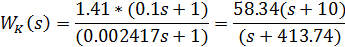
>> Wk=zpk([-10],[-413.74],1.41*0.1/0.002417)
Zero/pole/gain:
58.34 (s+10)
--------------
(s+413.7)
Аппроксимируем Wk(s) вышеописанным способом:
>> Wkd=c2d(Wk,0.0012,'tustin')
Zero/pole/gain:
47.0155 (z-0.9881)
------------------
(z-0.6023)
Sampling time: 0.0012
Раскроем скобки:
;
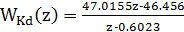Разделим полученное выражение на z:
;
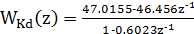Запишем разностное уравнение:
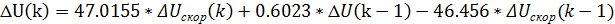
Полученное уравнение используем для реализации регулятора. Эта рекуррентная формула позволяет вести расчет в режиме реального времени.
Дата: 2019-12-10, просмотров: 257.
