Через частоту среза проходит прямая -20 Дб/дек. Это является обязательным условием для получения качественной системы. Из-за широкой среднечастотной части, перерегулирование будет малым.

Частота среза 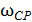находится графически. Отмечаем полученные точки на горизонтальной оси желаемой ЛАЧХ, проводим требуемые наклоны и получаем среднечастотную часть.

Высокочастотная часть желаемой ЛАЧХ имеет произвольный вид, т.к. она практически не влияет на качество САУ. Однако, для упрощения корректирующего устройства, необходимо стремиться к тому, что бы она совпадала по наклону с исходной ЛАЧХ в указанной области частот. При этом требуется, чтобы высокочастотная часть желаемой ЛАЧХ не заходила в запретную зону, образованную прямой с нулевым наклоном 0 Дб/дек.

По полученным точкам достраиваем высокочастотную часть желаемой ЛАЧХ и получаем желаемую логарифмическую амплитудную характеристику (рис. 3, ).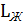

По виду получаемой желаемой ЛАЧХ записываем ПФ:

.

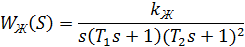
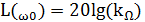Для того, чтобы правильно записать коэффициент в приведенной ПФ, осуществим переход от логарифмов:

; ;

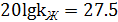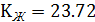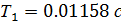
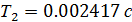
Подставляем полученные коэффициенты в выражение для 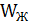 и получаем:

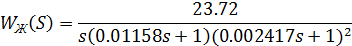
Определяем желаемую фазовую частотную характеристику. А также переходный процесс и показатели качества желаемой системы. Для этого занесем полученную ПФ 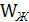 в MATLAB в zpk-форме:

>> Wzh=zpk ([],[0,-86.36,-413.74,-413.74],16.8/(0.01158*0.002417*0.002417))

 Zero/pole/gain:

 248340425.8576

-----------------------

s (s+86.36) (s+413.7)^2

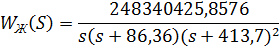
Определяем желаемую фазовую частотную характеристику (рис.9):

>> margin(Wzh);grid on

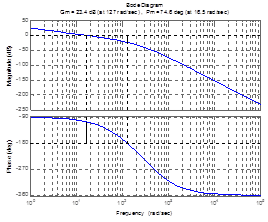
Рис.9

Запас устойчивости по фазе данной системы Δφ = 74.6⁰, запас по амплитуде ΔL = 23.4 Дб. Данная система устойчива.

Находим ПФ 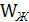 замкнутой системы:

>> Fzh=feedback(Wzh,1)

Zero/pole/gain:

 248340425.8576

---------------------------------------------

(s+47.2) (s+29.76) (s^2 + 836.9s + 1.768e005)

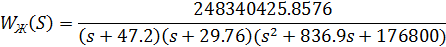
Переходная характеристика желаемой системы представлена на рис. 10.

>> step(Fzh);grid on

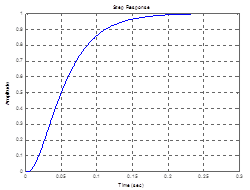
Рис.10

Время переходного процесса составляет 0,3 с. Оно характеризует быстродействие системы. Перерегулирование равно 0% - не превышает заданного 25%.

Исходя из вышеперечисленного можно сделать вывод, что система устойчива, так как переходный процесс является сходящимся. Таким образом, желаемая система автоматического управления удовлетворяет установленным к ней требованиям по быстродействию, перерегулированию и запасом устойчивости.

4. Синтез последовательного корректирующего устройства (регулятора)

Структурная схема САУ при последовательной коррекции изображена на рис. 11, где приняты следующие обозначения: 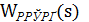- передаточная функция исходной системы; 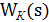- ПФ корректирующего устройства.

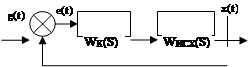Рис. 11. Структурная схема системы при последовательной коррекции.

Полагая, что ПФ скорректированной системы :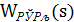

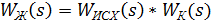
Переходя к логарифмическим характеристикам, после преобразований, получим:

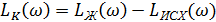
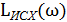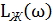Таким образом, графически вычитая  из и учитывая точки излома, получим ЛАЧХ корректирующего устройства (рис. 4,  ).

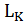По форме 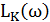 записываем ПФ корректирующего устройства :

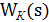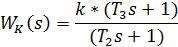
Коэффициент передачи корректирующего устройства определяется:

20lg K = 3;

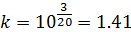
Подставив значения времени и коэффициента передачи в полученную ПФ корректирующего устройства:

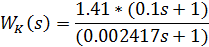
Существует три способа реализации:

1. Последовательная коррекция с помощью пассивных корректирующих звеньев;

2. Коррекция на основе активных фильтров (операционных фильтров);

3. Дискретная коррекция.