Для построения ЛАЧХ исходной системы, используем ПФ разомкнутой системы, полученную в предыдущем пункте:

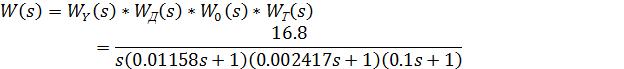
Основным достоинством логарифмических амплитудных частотных характеристик является возможность построения без применения вычислительной работы. Особенно когда ПФ может быть представлена в виде произведения сомножителей. Тогда результирующая ЛАЧХ может быть приближенно построена в виде асимптотической ЛАЧХ, представляющей собой совокупность отрезков прямых линий с наклоном [20 дБ/дек].

Определим точки излома и пересечения с осями логарифмической координатной сетки нашей ПФ.

Для построения ЛАЧХ находится величина:

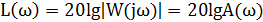
Определяем L(ω) при ω = 0;

L(ω)=20lgK=20lg16.8=20*1.225=24.5062

Постоянные времени:

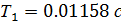
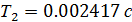
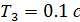
Находим точки излома исходной ЛАЧХ:

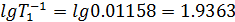
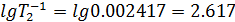
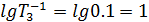
Используя полученные значения, строим ЛАЧХ исходной системы (рис. 4, Lисх).

Используем средства математического пакета MATLAB, в частности, приложением Control System Toolbox, для определения устойчивости и частотных характеристик исходной системы.

Занесем ПФ разомкнутой системы в MATLAB, обозначив ее через W.

W=zpk([],[0,-86.36,-413.74,-10],16.8/(0.01158*0.002417*0.1))

Zero/pole/gain:

 6002388.093

----------------------------

s (s+86.36) (s+413.7) (s+10)

Строим фазовую частотную характеристику (рис. 5), которую используют для определения фазового сдвига между входными и выходными колебаниями. Используем функцию margin.

>> margin(W); grid on

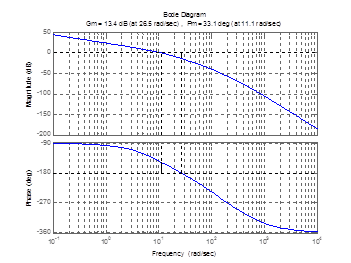
Рис. 5

Для определения запаса устойчивости определяют две величины: запас устойчивости по фазе Δφ и запас устойчивости по амплитуде ΔL.

Запас устойчивости по фазе определяется величиной Δφ, на которую должно возрасти запаздывание по фазе в системе на частоте среза 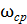, чтобы система оказалась на границе устойчивости.

Запас устойчивости по амплитуде определяется величиной ΔL допустимого подъема л.а.х., при котором система окажется на границе устойчивости.

По рис. 5 определим запас устойчивости по фазе и амплитуде. В нашем случае запас по фазе Δφ = 33.1, запас по амплитуде ΔL = 13.4 Дб. Данные параметры системы являются неудовлетворительными и не соответствуют рекомендуемым значениям Δφ = 40÷60⁰, следовательно система неустойчива.

Воспользуемся критерием Найквиста для определения устойчивости разомкнутой системы автоматического управления. Для этого построим годограф Найквиста от разомкнутой системы с помощью средств MATLAB (рис. 6). Используем функцию nyquist.

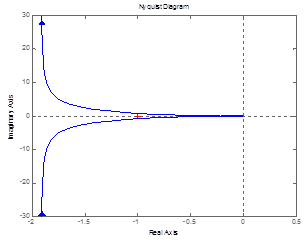
Рис.6

Увеличим область в начале координат.

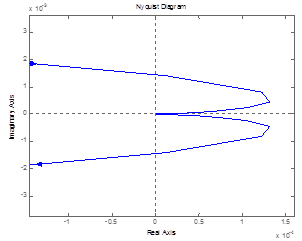
Рис.7

Точка с координатой (0;-j) охватывает годограф, следовательно, исходная система неустойчива.

Для определения переходного процесса найдем ПФ замкнутой исходной системы, обозначив ее через F. Для этого используем команду feedback.

>> F=feedback(W,1)

Zero/pole/gain:

 6002388.093

-----------------------------------------

(s+413.6) (s+88.99) (s^2 + 7.48s + 163.1)

Для определения времени, через которое наступит установившийся режим после подачи единичного ступенчатого воздействия строим переходную характеристику замкнутой системы, которая представлена рис. 8. При ее построении в MATLAB использовали функцию step.

>> step(F)

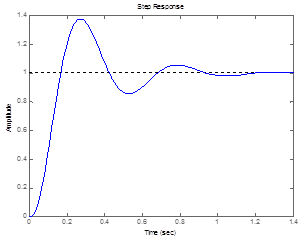
Рис. 8

Из рисунка видно, что процесс является сходящимся, (гармонические колебания затухают), а значит переходный процесс замкнутой системы устойчивый. Время переходного процесса 1,4 с.

Делая вывод из всего вышеперечисленного можно сказать, что система имеет характеристики не удовлетворяющие заданным параметрам. Для их улучшения необходимо в состав системы ввести дополнительно корректирующее звено (регулятор). Для этого, необходимо построить ЛАЧХ желаемой системы, с помощью которой получить ПФ корректирующего звена. Далее исследуем ПФ желаемой системы на критерий качества и реализуем корректирующее звено.