Общеизвестно, что на вступительных экзаменах в вузы часто встречаются задачи, которым в «традиционном» школьном курсе в силу различных причин уделяется мало внимания.
Одним из видов таких упражнений являются задачи, содержащие параметры. В школьных учебниках практически нет заданий на эту тему. Однако овладение методикой их решения мне кажется очень полезным: оно существенно повышает уровень логической подготовки учащихся, позволяет чуть по-новому, как бы изнутри взглянуть на такие «банальные» функциональные зависимости, подробно анализируемые школьной программой, как, к примеру, линейные и квадратные многочлены.
Уравнения и неравенства с параметрами. В подобного рода задачах встречаются два вида символов: неизвестные или переменные (обычно обозначаются буквами x , y , z ,…) и параметры (a , b , c ,…). Конечно разница между ними весьма условна, в известной степени можно сказать, что параметр – это переменная, значение которой считается фиксированным, и каждое значение параметра определяет относительно заданного неизвестного соответствующее уравнение (неравенство, систему). Иными словами, уравнение с параметром является фактически семейством уравнений, рассматриваемых при фиксированном значении параметра.
Введение параметра способствовало появлению качественно новых типов задач, вдохнуло, если так можно выразиться, новую жизнь в такие традиционные виды задач, как решение уравнений и неравенств.
1. Решить уравнение: 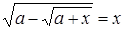 .
.
Решение. Возводим обе части в квадрат (условие 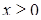 ):
):
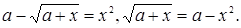
Еще раз возводим в квадрат (условие 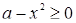 ). Получаем окончательное уравнение
). Получаем окончательное уравнение
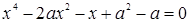 ,
,
среди решений, которого надо найти те, для которых 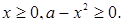 Получившееся уравнение имеет четвертую степень относительно неизвестного
Получившееся уравнение имеет четвертую степень относительно неизвестного 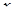 , но зато является квадратным относительно параметра
, но зато является квадратным относительно параметра  . Попробуем этим обстоятельством воспользоваться:
. Попробуем этим обстоятельством воспользоваться:
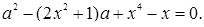
Найдем дискриминант:
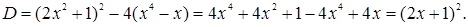
Теперь левая часть уравнения раскладывается на множители
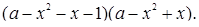
Наше уравнение распадается на два:
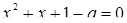 и
и 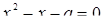 ,
,
каждое из которых надо решить при условии, что 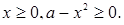
Начнем с уравнения 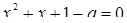 . Поскольку
. Поскольку 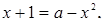 то из того, что
то из того, что 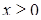 , следует, что
, следует, что 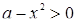 . Значит, нам достаточно найти лишь те решения, для которых
. Значит, нам достаточно найти лишь те решения, для которых 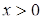 ; тогда неравенство
; тогда неравенство 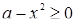 будет выполняться автоматически. Но сумма корней (если они есть) равна
будет выполняться автоматически. Но сумма корней (если они есть) равна 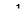 ; следовательно, уравнение
; следовательно, уравнение 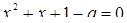 может иметь лишь один неотрицательный корень при условии
может иметь лишь один неотрицательный корень при условии 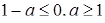 . Значит, при
. Значит, при 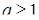 будет
будет 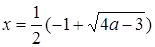 .
.
Перейдем ко второму уравнению 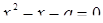 . Из этого уравнения
. Из этого уравнения 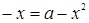 . Левая часть неположительная, правая неотрицательная. Равенство возможно лишь, если
. Левая часть неположительная, правая неотрицательная. Равенство возможно лишь, если 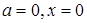 .
.
Ответ. Если 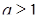 , то
, то 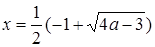 ;
;
если 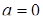 , то
, то 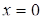 ;
;
при остальных 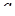 решений нет [21].
решений нет [21].
2. При каких значениях параметра а уравнение  имеет корни сумма которых равна нулю?
имеет корни сумма которых равна нулю?
Решение. Это уравнение – квадратное, его дискриминант
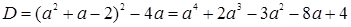 .
.
Сумма корней уравнения равна 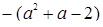 и по условию задачи она равна нулю, т.е.
и по условию задачи она равна нулю, т.е. 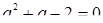 , что возможно при
, что возможно при 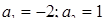 . Теперь необходимо осуществить контроль неотрицательности дискриминанта при этих значениях
. Теперь необходимо осуществить контроль неотрицательности дискриминанта при этих значениях 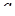 . При
. При 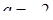 дискриминант
дискриминант 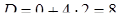 положителен, тогда как при
положителен, тогда как при 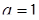 дискриминант
дискриминант 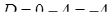 оказывается отрицательным.
оказывается отрицательным.
Ответ. 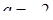 [3].
[3].
3. При каких значениях параметра 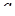 квадратное уравнение
квадратное уравнение  имеет корни одного знака?
имеет корни одного знака?
Решение. Так как по условию задачи рассматриваемое уравнение – квадратное, то 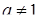 (иначе формулировка задачи не имеет смысла). Очевидно, условие задачи предполагает также существование корней квадратного уравнения, что означает неотрицательность дискриминанта. Если
(иначе формулировка задачи не имеет смысла). Очевидно, условие задачи предполагает также существование корней квадратного уравнения, что означает неотрицательность дискриминанта. Если 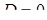 , то квадратное уравнение имеет один корень (два равных корня).
, то квадратное уравнение имеет один корень (два равных корня).
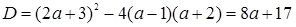
Так как по условию корни должны быть одинаковых знаков, то
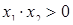 , т.е.
, т.е. 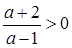 .
.
Решением последнего неравенства является
 .
.
С учетом условий 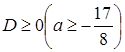 и
и 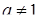 получим
получим 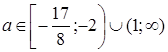 .
.
Ответ. 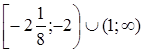 [7].
[7].
4. Для каждого неотрицательного значения параметра 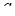 решить неравенство
решить неравенство  .
.
Решение. Левая часть неравенства представляет собой многочлен как относительно 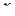 , так и относительно параметра
, так и относительно параметра 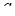 . Степени соответственно равны 4 и 3. Однако если умножить многочлен на
. Степени соответственно равны 4 и 3. Однако если умножить многочлен на 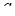 , а затем сделать замену
, а затем сделать замену 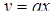 , то в новом многочлене максимальная степень параметра
, то в новом многочлене максимальная степень параметра 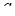 будет равна 2. Случай
будет равна 2. Случай 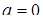 дает нам ответ
дает нам ответ 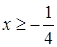 . Будем теперь считать, что
. Будем теперь считать, что 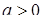 . Умножив обе части неравенства на
. Умножив обе части неравенства на 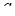 и сделав замену
и сделав замену 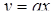 , получим
, получим
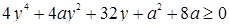 .
.
Левая часть представляет собой квадратный трехчлен относительно 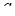 :
:
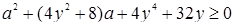 ,
,
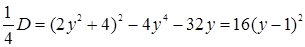 .
.
Раскрывая левую часть неравенства на множители, получим
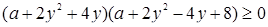 ,
,
или
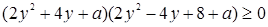 .
.
Второй множитель положителен при всех 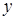 , если
, если 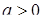 . Приходим к неравенству
. Приходим к неравенству 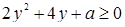 , откуда, если
, откуда, если 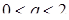 ,
, 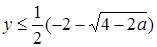 ; если
; если 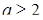 ,
, 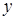 ‑ любое. Возвращаясь к
‑ любое. Возвращаясь к 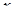 , получим ответ.
, получим ответ.
Ответ. Если 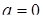 , то
, то 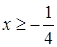 ;
;
если 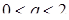 , то
, то 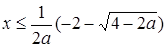 ;
;
если 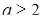 , то
, то  ‑ любое [21].
‑ любое [21].
5. Найти все значения параметра 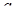 , при которых существует единственное значение
, при которых существует единственное значение 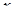 , при котором выполняется неравенство
, при котором выполняется неравенство
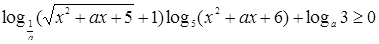 .
.
Решение. Обозначим 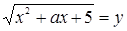 (
( 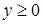 ) и перейдем к основанию 5. Получим:
) и перейдем к основанию 5. Получим:
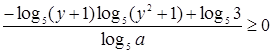 .
.
Функция от 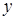 , расположенная в числителе, монотонно убывает. Нетрудно подобрать значение
, расположенная в числителе, монотонно убывает. Нетрудно подобрать значение 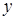 , при котором она обращается в нуль:
, при котором она обращается в нуль: 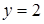 .
.
Если 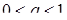 , то решением неравенства относительно
, то решением неравенства относительно 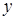 будет
будет 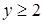 , а следовательно, исходное неравенство не может иметь единственного решения. (Неравенство
, а следовательно, исходное неравенство не может иметь единственного решения. (Неравенство 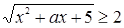 при любом
при любом 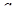 имеет бесконечно много решений.)
имеет бесконечно много решений.)
Значит, 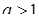 и решением относительно
и решением относительно 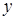 будет
будет 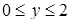 . Возвращаясь к
. Возвращаясь к 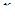 , будем иметь
, будем иметь 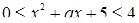 . Для того чтобы существовало единственное значение
. Для того чтобы существовало единственное значение 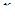 , удовлетворяющее последним неравенствам, необходимо и достаточно, чтобы наименьшее значение квадратного трехчлена
, удовлетворяющее последним неравенствам, необходимо и достаточно, чтобы наименьшее значение квадратного трехчлена 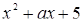 равнялось бы 4, т.е.
равнялось бы 4, т.е. 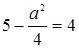 .
.
Ответ. 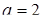 [5].
[5].
6. Найти все значения 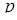 , при каждом из которых множество решений неравенства
, при каждом из которых множество решений неравенства 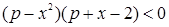 не содержит ни одного решения неравенства
не содержит ни одного решения неравенства 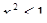 .
.
Решение. Нам надо найти все 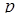 , такие, что при всех
, такие, что при всех 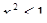 имеет место неравенство
имеет место неравенство 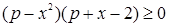 . Решение последнего неравенства при данном
. Решение последнего неравенства при данном 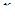 относительно
относительно 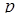 состоит из двух лучей, исключается внутренняя часть отрезка с концами
состоит из двух лучей, исключается внутренняя часть отрезка с концами 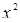 и
и 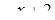 (какой из них левый, а какой правый‑неважно). Но если
(какой из них левый, а какой правый‑неважно). Но если 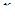 меняется от ‑1 до 1, то
меняется от ‑1 до 1, то 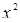 меняется от 0 до 1, а
меняется от 0 до 1, а 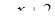 меняется от 1 до 3. Теперь понятно, что
меняется от 1 до 3. Теперь понятно, что 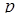 не может принимать значения от 0 до 3, а при всех
не может принимать значения от 0 до 3, а при всех 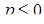 или
или 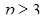 заданное условие выполняется.
заданное условие выполняется.
Ответ. 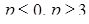 [22].
[22].
Графические методы решения задач с параметрами. Задачи с параметрами требуют к себе своеобразного подхода по сравнению с остальными – здесь необходимо грамотное и тщательное исследование. Для применения графических методов требуется умение выполнять построение различных графиков, вести графическое исследование, соответствующее данным значениям параметра.
1. При каких значениях параметра 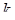 уравнение
уравнение 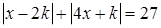 имеет ровно 2 решения?
имеет ровно 2 решения?
Решение. Рассмотрим функцию 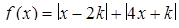 .
.
Графиком такой функции является ломанная из трех звеньев. Найдем точки излома:
1) 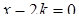 ;
;
2) 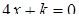 .
.
Так как 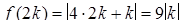 ;
; 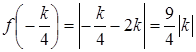 , то
, то 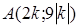 и
и 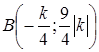 ‑ точки излома. Заметим, что
‑ точки излома. Заметим, что 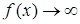 , если
, если 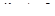 и
и 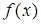 имеет минимум в одной из точек
имеет минимум в одной из точек 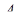 или
или 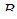 .
.
С геометрической точки зрения количество решений уравнения 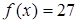 ‑ это количество точек пересечения при каждом фиксированном значении параметра
‑ это количество точек пересечения при каждом фиксированном значении параметра 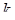 ‑ ломанной, состоящей из трех звеньев, и прямой
‑ ломанной, состоящей из трех звеньев, и прямой 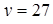 .
.

По рис. 4 видно, что уравнение  имеет ровно 2 решения, если значение в точке минимума меньше 27. Причем значение в другой из точек излома несущественно. Значит необходимо выполнение одного из двух неравенств:
имеет ровно 2 решения, если значение в точке минимума меньше 27. Причем значение в другой из точек излома несущественно. Значит необходимо выполнение одного из двух неравенств:
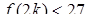 или
или 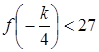 .
.
Так как 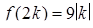 , то первое неравенство равносильно неравенству
, то первое неравенство равносильно неравенству 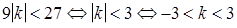 . А поскольку
. А поскольку 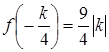 , то второе неравенство равносильно неравенству
, то второе неравенство равносильно неравенству
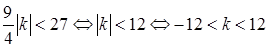 .
.
Объединением полученных интервалов будет интервал 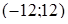 .
.
Ответ. Уравнение имеет два решения при 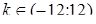 [7].
[7].
2. При любом значении параметра 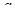 решить неравенство
решить неравенство
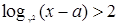 .
.
Решение. Рассмотрим плоскость 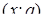 и изобразим на ней множество точек, координаты которых удовлетворяют неравенству рис.5. Сначала изобразим область, для точек которой имеет смысл
и изобразим на ней множество точек, координаты которых удовлетворяют неравенству рис.5. Сначала изобразим область, для точек которой имеет смысл 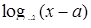 . Это будет полуплоскость
. Это будет полуплоскость 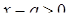 (правее и ниже прямой
(правее и ниже прямой 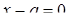 ), из которой удалены части прямых
), из которой удалены части прямых 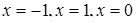 . Вне полосы, ограниченной прямыми
. Вне полосы, ограниченной прямыми 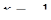 и
и 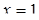 , будет
, будет 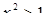 , и, следовательно, после потенцирования неравенства получим
, и, следовательно, после потенцирования неравенства получим 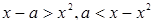 .
.
Последнему неравенству соответствует область под параболой 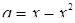 (при этом
(при этом 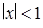 ).
).
Внутри полосы 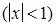 будет
будет 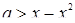 . На рисунке 5 область
. На рисунке 5 область 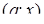 , для точек которой
, для точек которой 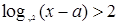 , заштрихована. (Заметим, что парабола
, заштрихована. (Заметим, что парабола 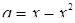 касается прямой
касается прямой  ) Теперь ось
) Теперь ось 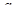 точками
точками 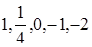 разбита на шесть участков, на каждом из которых легко выписывается решение нашего неравенства. Для этого берем
разбита на шесть участков, на каждом из которых легко выписывается решение нашего неравенства. Для этого берем  на соответствующем участке, проводим горизонтальную прямую, находим значения
на соответствующем участке, проводим горизонтальную прямую, находим значения  , соответствующие концам отрезков этой прямой, попавших в заштрихованную зону.
, соответствующие концам отрезков этой прямой, попавших в заштрихованную зону.

Например, если 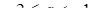 , то получаем два отрезка, концы первого:
, то получаем два отрезка, концы первого: 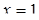 и
и 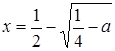 (меньший корень уравнения
(меньший корень уравнения 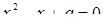 ), второго:
), второго: 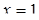 и
и 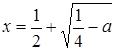 .
.
Ответ. Если 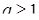 ,
,  , решений нет;
, решений нет;
если 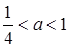 , то
, то 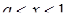 ;
;
если 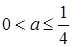 , то
, то 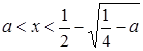 и
и 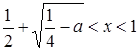 ;
;
если 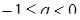 , то
, то 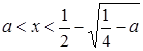 и
и 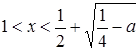 ;
;
если 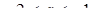 , то
, то 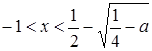 и
и 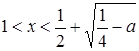 ;
;
если 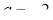 , то
, то  ;
;
если 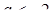 , то
, то 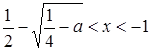 и
и 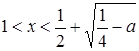 [4].
[4].
Дата: 2019-12-10, просмотров: 390.