Уравнения и неравенства ‑ традиционная тема школьного курса математики, занимающая большое место, начиная с младших классов, где простейшие уравнения и неравенства до введения теории на основе свойств арифметических действий, и кончая старшими классами, где решаются трансцендентные уравнения.
Уравнения и неравенства представляют собой тот алгебраический аппарат, тот язык, на который переводятся разного рода задачи, в том числе и прикладные, строятся их математические модели.
Использование монотонности функций при решении уравнений и неравенств. Одну из наиболее часто встречающихся идей хорошо иллюстрирует решение следующего простого неравенства:
1. Решить неравенство: 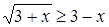 .
.
Решение. Есть два стандартных пути решения: возведение в квадрат (при условии  ; если же
; если же 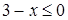 , неравенство выполняется) и замена неизвестного
, неравенство выполняется) и замена неизвестного 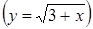 .
.
Рассмотрим еще один способ – нестандартный. Функция, расположенная в левой части, монотонно возрастает, в первой части убывает. Из очевидных графических соображений следует, что уравнение 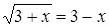 имеет не более одного решения, причем если x0 – решение этого уравнения, то при
имеет не более одного решения, причем если x0 – решение этого уравнения, то при 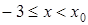 будет
будет 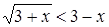 , а решением данного неравенства будет
, а решением данного неравенства будет 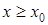 . Значение x0 легко подбирается: x0 = 1.
. Значение x0 легко подбирается: x0 = 1.
Ответ. 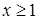 [16].
[16].
2. Решить уравнение: 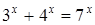 .
.
Решение. Данное уравнение имеет очевидное решение x = 1. Докажем, что других решений нет. Поделим обе части на 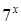 , получим
, получим 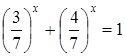 . Левая часть представляет собой монотонно убывающую функцию. Следовательно, каждое свое значение она принимает один раз, т.е. данное уравнение имеет единственное решение.
. Левая часть представляет собой монотонно убывающую функцию. Следовательно, каждое свое значение она принимает один раз, т.е. данное уравнение имеет единственное решение.
Ответ. x = 1.
Итак, основная идея, на которой основывались решения этих двух примеров, весьма проста: если f( x) монотонно возрастает, а φ(x) монотонно убывает, то уравнение f( x) = φ( x) имеет не более одного решения, причем если x = x0 – решение этого уравнения, то при x > x0 (x входит в область определения обеих функций f( x) и φ( x)) будет f( x) > φ( x), а при x < x0 будет
f( x) < φ( x).
Стоит обратить внимание на одну модификацию этой идеи, а именно: если f( x) – монотонная функция, то из равенства f( x) = f( y) следует, что x = y [8].
3. Решить уравнение: 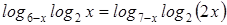 .
.
Решение. Преобразуем уравнение:
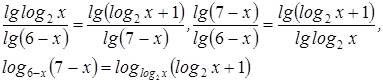 .
.
Рассмотрим функцию 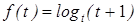 .
.
Докажем, что при t > 1 эта функция монотонно убывает. Это можно сделать, например, стандартным образом: найти производную 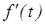
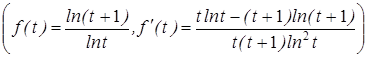
и доказать, что при t > 1 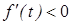 . Покажем другой способ:
. Покажем другой способ:
 .
.
Получившаяся функция, очевидно, является убывающей (основание растет, под знаком логарифма функция убывает).
Наше уравнение имеет вид: 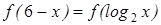 , значит,
, значит, 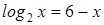 . Слева функция возрастающая, следовательно, решение единственно, оно легко находится подбором: x = 4.
. Слева функция возрастающая, следовательно, решение единственно, оно легко находится подбором: x = 4.
Ответ. x = 4 [13].
Уравнения вида f( f ( x) ) = x. При решении уравнений указанного вида полезна бывает теорема:
Если y = f(x) – монотонно возрастающая функция, то уравнения
f( x) = x (А)
и
f ( f ( x)) = x (Б)
эквивалентны.
Доказательство. То, что уравнение (Б) является следствием уравнения (А), очевидно: любой корень (А) удовлетворяет (Б). (Если
f ( x0) = x0, то f ( f ( x0)) = f ( x0) = x0.). Докажем, что любой корень уравнения (Б) удовлетворяет уравнению (А). Пусть x0 такое, что f ( f ( x0)) = x0.Предположим, что f ( x0) ≠ x0 и для определенности f ( x0) > x0. Тогда f ( f ( x0)) > f ( x0) > x0, что противоречит предположению ( f ( f ( x0)) = x0). Теорема доказана.
Верна ли теорема для монотонно убывающей функции?
Замечание. Если y = f ( x) монотонно возрастает, то при любом k уравнения 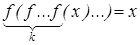 и f ( x) = x эквивалентны.
и f ( x) = x эквивалентны.
Приведем несколько примеров использования этой теоремы [22].
1. Решить уравнение: 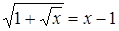 .
.
Решени е. Перепишем уравнение 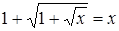 . Рассмотрим функцию
. Рассмотрим функцию 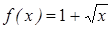 . Эта функция монотонно возрастает. Имеем уравнение
. Эта функция монотонно возрастает. Имеем уравнение
f ( f ( x)) = x. В соответствии с теоремой заменяем его на эквивалентное уравнение f ( x) = x или  .
.
Ответ.
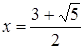 .
.
2. Решить уравнение:
 .
.
Решение. Преобразуем уравнение: 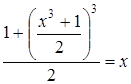 .
.
Данное уравнение имеет вид: f ( f ( x)) = x, где  .
.
Согласно теореме имеем эквивалентное уравнение: 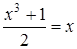 ,
,
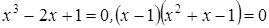 .
.
Ответ. 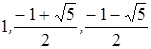 [14].
[14].
3. Решить систему уравнений:  .
.
Решение. Рассмотрим функцию 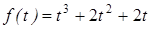 . Поскольку
. Поскольку
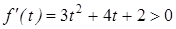 при всех t, то f ( t) возрастает.
при всех t, то f ( t) возрастает.
Система имеет вид y = f ( x), z = f ( y), x = f ( z), т.е. x = f ( f ( f ( x))).
Согласно теореме x удовлетворяет уравнению f ( x) = x или 
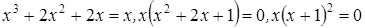 .
.
Ответ. (0, 0, 0), (-1, -1, -1).
Использование экстремальных свойств рассматриваемых функций. Оценки. Основные идеи этого пункта достаточно хорошо видны из примеров:
1. Решить уравнение: 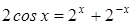 .
.
Решение. Левая часть данного уравнения не превосходит 2, а правая- не меньше 2. Следовательно, равенство может иметь место лишь при условии, что левая и правая части равны 2, т.е. x = 0.
Замечание. Данная ситуация, когда наименьшее значение функции, расположенной в одной части уравнения, равно наибольшему значению функции, расположенной в другой части, может быть обобщена. Более общий случай – уравнения вида f ( x) = φ ( x), для которых  при всех допустимых x (формально мы можем переписать это уравнение в виде
при всех допустимых x (формально мы можем переписать это уравнение в виде
f ( x) = φ ( x) = 0, в результате приходим к уже рассмотренной ситуации, поскольку наибольшее значение правой части равно нулю).
2. Решить уравнение: 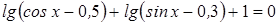 .
.
Докажем, что данное уравнение не имеет решений. Перейдем к следствию (потенцируем):  .
.
Оценим левую часть на основании неравенства между средним геометрическим и средним арифметическим
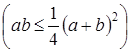 :
:
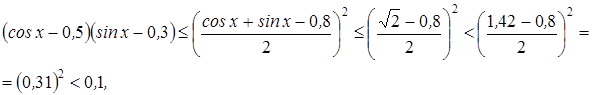

т.е. левая часть меньше правой. Уравнение не имеет решений.
Ответ. Нет решения.
3. Решить систему уравнений: 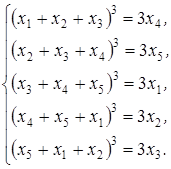
Решение. Докажем, что 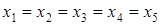 .
.
Пусть для определенности x5 > x4, тогда из первых двух уравнений получим 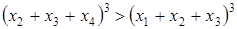 , откуда
, откуда 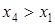 и тем более
и тем более 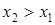 . Далее из третьего и четвертого получаем
. Далее из третьего и четвертого получаем 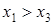 и тем более
и тем более 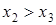 . Из последней пары находим
. Из последней пары находим 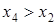 . Получилось противоречие (
. Получилось противоречие ( 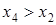 и
и  , т.е.
, т.е. 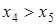 , а предположили, что
, а предположили, что 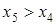 ).
).
Значит,  , отсюда
, отсюда  и т.д., все неизвестные равны между собой.
и т.д., все неизвестные равны между собой.
Ответ. (0, 0, 0, 0,0); 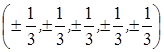 .
.
Нестандартные по формулировке задачи, связанные с уравнениями или неравенствами. К данной категории, в частности, относятся задачи, в которых требуется определить число корней заданного уравнения, доказать существование корня на определенном промежутке, решить уравнение или неравенство на заданном промежутке. Рассмотрим несколько примеров.
1. Доказать, что уравнение 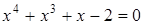 имеет одно положительное решение и одно отрицательное решение.
имеет одно положительное решение и одно отрицательное решение.
Решение. Единственность положительного решения достаточно очевидна. Это следует из того, что 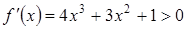 при
при  , где f ( x )-левая часть заданного уравнения, т.е. f ( x ) при
, где f ( x )-левая часть заданного уравнения, т.е. f ( x ) при 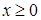 монотонно возрастает, а
монотонно возрастает, а 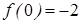 .
.
Докажем единственность отрицательного корня. Можно поступить следующим образом. Рассмотрим функции
 .
.
Докажем, что если  , то
, то 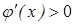 . (Из этого будет следовать наше утверждение, поскольку в данном случае
. (Из этого будет следовать наше утверждение, поскольку в данном случае 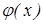 возрастает везде, где
возрастает везде, где 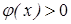 .)
.)
Имеем 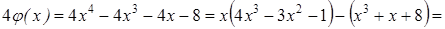
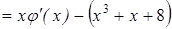 .
.
Значит, 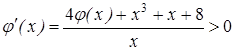 при
при 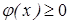
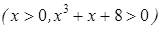 .
.
Утверждение доказано.
2. Найти все целые значения x, удовлетворяющие неравенству
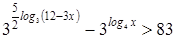 .
.
Решение. Область определения левой части неравенства  . Значит, нам достаточно рассмотреть три значения x: 1, 2, 3.
. Значит, нам достаточно рассмотреть три значения x: 1, 2, 3.
Если 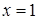 , то левая часть равна
, то левая часть равна 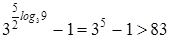 .
.
Если 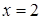 , то
, то 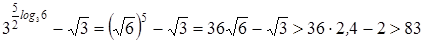 .
.
Если  , то
, то 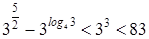 .
.
Ответ. 1; 2.
3. Найти все целые x, удовлетворяющие неравенству
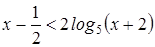 .
.
Решение. Рассмотрим функцию 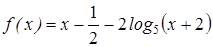 .
.
Докажем, что, начиная с некоторого x, f ( x) возрастает. Это можно было сделать обычным путем, оценивая производную. Мы сделаем иначе. Нам достаточно доказать возрастание функции для целых x, т.е. что
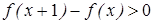 .
.
Имеем 
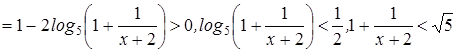 .
.
Последнее неравенство выполняется при 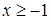 , т.е. для всех допустимых целых x.
, т.е. для всех допустимых целых x.
Нам осталось найти наибольшее целое, для которого 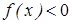 (или наименьшее, для которого
(или наименьшее, для которого 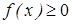 ).
).
Докажем, что
 . Далее,
. Далее, 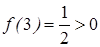 .
.
Ответ. -1, 0, 1, 2 [22].
Тригонометрические уравнения. К нестандартным следует отнести также уравнения, содержащие обратные тригонометрические функции.
1. Решить уравнение: 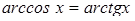 .
.
Решение. По определению обратных тригонометрических функций
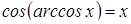 . Найдем
. Найдем 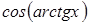 .
.
Эта задача сводится к следующей: «Найти cos α, если 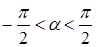 и
и
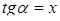 (
( 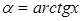 )».
)».
Поскольку cos α >0, то 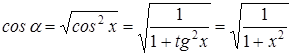 .
.
Получаем уравнение 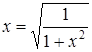 , откуда
, откуда  . Получаем для x два значения:
. Получаем для x два значения:
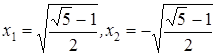 .
.
Второе значение для x не подходит, поскольку 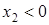 .
.
Ответ. 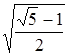 .
.
Замечание. Данное уравнение можно решить и иначе. Обозначим левую и правую части данного уравнения через y . Тогда 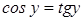 . Для y имеем тригонометрическое уравнение, сводящееся к квадратному относительно
. Для y имеем тригонометрическое уравнение, сводящееся к квадратному относительно
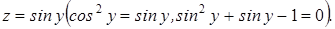
По смыслу задачи 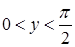 , следовательно,
, следовательно, 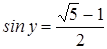 , значит,
, значит,
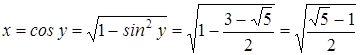 .
.
Не так уж редко встречаются уравнения, решение которых основывается на ограниченности функций cos x и sin x .
2. Решить уравнение: 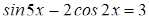 .
.
Решение. Поскольку 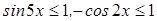 , то левая часть не
, то левая часть не
превосходит 3 и равна 3, если  .
.
Для нахождения значений x, удовлетворяющих обоим уравнениям, поступим следующим образом. Решим одно из них. Затем среди найденных значений отберем те, которые удовлетворяют и другому.
Начнем со второго: 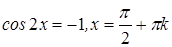 .
.
Тогда 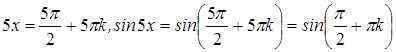 .
.
Понятно, что лишь для четных k будет 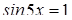 .
.
Ответ.  [2].
[2].
4. Найти в градусах корень уравнения:  , если
, если 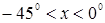 .
.
Решение. Уравнение является однородным второго порядка. Разделив обе части на 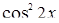 , получим уравнение
, получим уравнение 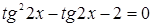 , квадратное относительно
, квадратное относительно 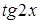 . Решив его, найдем
. Решив его, найдем

По условию 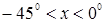 , значит,
, значит, 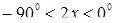 . При этих значениях аргумента
. При этих значениях аргумента 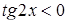 , следовательно, уравнение
, следовательно, уравнение 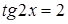 не имеет решения.
не имеет решения.
Из уравнения 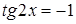 находим
находим  . Значит,
. Значит, 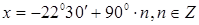 . Придавая
. Придавая 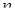 значения
значения  , выбираем
, выбираем 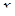 , удовлетворяющие условию
, удовлетворяющие условию 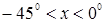 . При
. При  получим
получим 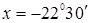 .
.
Ответ. 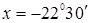 [17].
[17].
Тригонометрические неравенства. Тригонометрическими неравенствами называются неравенства вида 
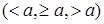 , где
, где 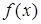 ‑ одна из тригонометрических функций
‑ одна из тригонометрических функций 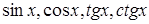 . При решении этих неравенств удобно использовать график соответствующей тригонометрической функции.
. При решении этих неравенств удобно использовать график соответствующей тригонометрической функции.
1. Решить неравенство: 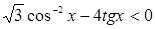 .
.
Решение. Здесь должно выполняться условие 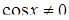 , т.е.
, т.е. 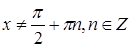 . Произведем преобразования:
. Произведем преобразования:
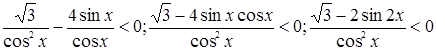 .
.
Так как  при
при 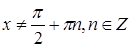 , то достаточно решить неравенство
, то достаточно решить неравенство 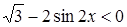 , т.е.
, т.е. 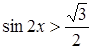 . Полагая
. Полагая 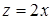 и построив график функции
и построив график функции 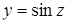 (рис. 2), устанавливаем, что
(рис. 2), устанавливаем, что 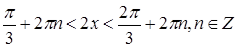

или  . В эти интервалы значения
. В эти интервалы значения 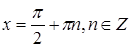 не входят.
не входят.
Ответ.  , где
, где 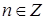 .
.
2. Решить неравенство:  .
.
Решение. Преобразуем левую часть равенства:

Остается решить неравенство 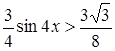 , т.е.
, т.е. 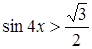 . Полагая
. Полагая 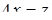 и построив график функции
и построив график функции  (рис.2) находим
(рис.2) находим
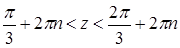
или 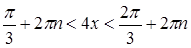 . Отсюда
. Отсюда 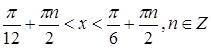 .
.
Ответ. 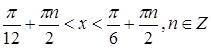 .
.
3. Решить неравенство:  .
.
Решение. Последовательно преобразуя левую часть неравенства, получим
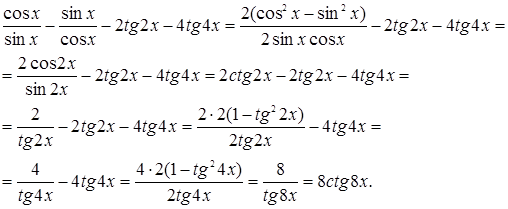
Итак, имеем неравенство 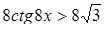 или
или  . Полагая
. Полагая 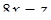 , с помощью графика функции
, с помощью графика функции 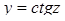 (рис.3),
(рис.3),

устанавливаем, что
 , откуда
, откуда 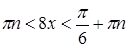 , т.е.
, т.е. 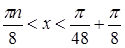 ,
, 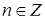 .
.
Ответ. 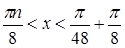 ,
, 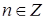 [6].
[6].
Дата: 2019-12-10, просмотров: 368.