С чего начинать решение задачи? Движение вашей мысли, как заметил известный советский психолог П.Я. Гальперин, не должно быть «броуновским», т.е. беспорядочным. Главное - нужно сделать глубокий и всесторонний анализ задачи.

Решить математическую задачу ‑ это значит найти такую последовательность общих положений математики (определений, аксиом, теорем, правил, законов, формул), применяя которые к условиям задачи или к их следствиям (промежуточным результатам решения) получаем то, что требуется в задаче, ‑ ее ответ.

Основными методами поиска решения задач являются анализ и синтез. Благодаря анализу осуществляется целенаправленная актуализация знаний (знания актуализируются не механически, наугад, «вслепую», а в связи с потребностью в них). В ходе анализа естественно определяются момент использования знаний (не тогда, когда вспоминаешь, а тогда, когда нужно), выбор знаний (берутся лишь те знания, в которых возникла потребность при анализе), форма использования знаний (не так, как в учебнике, а в том виде, в каком это удобнее для решения задачи) и характер использования знаний (все сразу или поочередно).

Ранее были рассмотрены анализ Паппа и анализ Евклида. Они применимы и при поиске решений задач. Каждый из этих анализов имеет свою область применения. Например, при поиске решений текстовых задач с помощью уравнений более удобным является анализ Евклида: искомая величина обозначается через х и на основе текста задачи выводятся следствия до тех пор, пока не будет получено уравнение, связывающее искомую величину х с данными величинами. Поиск решения текстовых задач (решаемых арифметическими средствами) удобнее вести с помощью анализа Паппа. Поиск решения таких задач начинают с вопроса задачи и определяют, какие величины надо знать, чтобы ответить на этот вопрос. Далее выясняют, являются ли эти величины известными. Если некоторые из них не даны в условии задачи, то ставится вопрос, как можно найти такие величины, что необходимо знать для этого. Подобные вопросы повторяют до тех пор, пока не обнаружится, что нахождение «промежуточных» неизвестных величин сводится к вычислениям с данными величинами.

Таким образом, при решении задач можно выделить следующие общие приемы мыслительной деятельности: первый прием - прием развертывания термина, он состоит в выведении всевозможных следствий из условия задачи или в выяснении всевозможных свойств объектов, о которых говорится в задаче. Второй прием - анализ через синтез - «челнок» состоит в чередовании восходящего анализа и синтетических рассуждений. Эти два приема подводят к формированию плана решения задачи. Третий прием - прием построения дедуктивных умозаключений. Именно эти приемы должны быть отработаны с учащимися.

В заключение отметим, что большинство приемов поиска решения задач базируется на достаточно серьезном логическом содержании, поэтому овладение ими учащимися возможно лишь при условии систематического и целенаправленного их применения. Полезно практиковать в этих целях краткий методологический комментарий, разъясняющий учащимся суть применяемых приемов поиска решения задач [10,12].

Сам процесс решения задач при определенной методике оказывает весьма положительное влияние на умственное развитие детей, поскольку он требует выполнения умственных операций анализа и синтеза, абстрагирования и конкретизации, сравнения, обобщения.

Существуют различные методические подходы к обучению детей решению текстовых задач. Но какую бы методику обучения ни выбрал учитель, ему надо знать, как построены такие задачи, и уметь их решать разными способами.

Итак, любая текстовая задача – как считает Л.П. Стойлова – есть описание на естественном языке какого-либо явления (ситуации или процесса) с требованием дать количественную характеристику какого-либо компонента этого явления, установить наличие или отсутствие некоторого отношения между компонентами или определить вид этого отношения. М.И. Моро, А.М. Пышкало определяют задачу, как сформулированный словами вопрос, ответ на который может быть получен с помощью арифметических действий.

Прежде всего, каждая задача включает числа: данные и искомые. Числа в задаче характеризуют численности множеств или значения величины, выражают отношение или являются отвлеченными данными числами.

Каждая задача имеет условие и вопрос. В условии задачи указываются связи между данными числами, а так же между данными и искомыми; эти связи и определяют выбор соответствующих арифметических действий. Вопрос указывает, какое число является искомым. Исходя из этого, И.Б. Истомина считает, что любое математическое задание можно рассматривать, как задачу, выделив в нем условие и требование.

Уточним теперь смысл термина «решение задачи». Так сложилось, что этим термином обозначают разные понятия:

1) решением задачи называют результат, т.е. ответ на требование задачи, на поставленный в ней вопрос. Чаще всего дети понимают под решением задачи ответ на поставленный ней вопрос.

2) решением задачи называют процесс нахождения этого результата, причем этот процесс рассматривается двояко: и как метод нахождения результата, (например, говорят о решении задачи арифметическим способом) и как последовательность действий, которые выполнит решающий, применяя тот или иной метод (т.е. в данном случае под решением задачи понимается вся деятельность человека, решающего задачу).

Довольно часто бывает так, что как только учитель сообщил задачу, дети сразу же дают ответ на ее вопрос. Но это далеко не всегда удовлетворяет учителя. Он стремится выяснить, как получен ответ, на основе каких рассуждений, с помощью какого арифметического действия и т.п. сначала учитель требует обычно «полного» ответа на вопрос. Это имеет смысл не только с точки зрения развития устной речи учащегося, но и для того, чтобы дети еще раз вернулись мысленно к тексту задачи, сопоставляли свой ответ с условием и вопросом задачи. Получив ответ, учитель продолжает спрашивать: «Как ты это узнал?» Этот, казалось бы, простой вопрос нередко для ученика бывает трудным: «Я догадался», «Я посчитал» - вот типичные ответы первоклассников в подобных случаях (а иногда и просто «Я не знаю») Среди учителей было распространено мнение, что если ученик не может объяснить, как получил ответ на вопрос задачи, значит, он не решил ее. Дети внутренне не могут с этим согласиться. Возникает своего рода конфликтная ситуация, которая в данном случае совсем не полезна. Причина ее заключается в том, что учитель понимает требование решить задачу значительно шире, чем просто дать ответ на ее вопрос.

Для того, чтобы такого взаимонепонимания между учителем и учащимся не возникало, необходимо разъяснить детям смысл требование «решить задачу». Полезно, например, сказать детям следующее: «Задачи, которые вы решаете на уроках математики, - это не загадки, которые надо разгадать». Решить задачу – это значит объяснить какие действия нужно выполнить над данными в ней числами, чтобы после вычислений получить число, которое в ней нужно узнать. Записать решение задачи – значит с помощью цифр и знаков действий показать, что нужно сделать, чтобы найти неизвестное число, выполнить вычисление и дать ответ на вопрос задачи.

Научить детей решать задачи ‑ значит научить их устанавливать связи между данными и искомым и в соответствии с этим выбирать, а затем и выполнять арифметические действия.

Чтобы добиться этого, учитель должен предусмотреть в методике обучения решению задач одного вида ступени, имеющие свои цели.

На первой ступени учитель ведет подготовку к решению задач рассматриваемого вида. На этой ступени дети должны усвоить связи, на основе которых они будут выбирать действия при решении таких задач.

На второй ступени учитель знакомит учеников с решением задач рассматриваемого вида. Здесь дети учатся переходить от конкретной ситуации, выраженной в задаче, к выбору соответствующего арифметического действия.

На третьей ступени учитель формирует умение решать задачи рассматриваемого вида. Учащиеся должны научиться решать любую задачу независимо от ее конкретного содержания.

Особенность решения сюжетной задачи состоит в том, что решаются, вообще говоря, две разные, хотя и взаимосвязанные проблемы: перевод содержания задач на язык математики (то есть математизация содержания) и решения собственно математической задачи средствами математики, что образует процесс сложной умственной деятельности. Чтобы овладеть им, надо знать основные этапы решения задачи и некоторые приемы их выполнения [11,15].

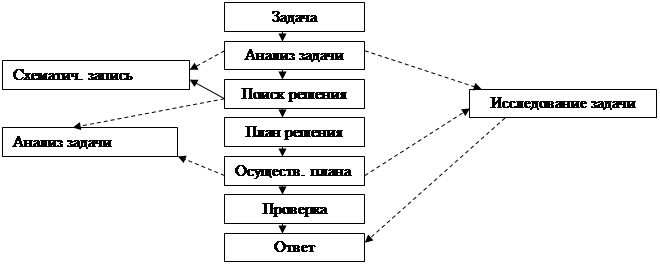
Структуру процесса решения задачи можно представить в виде следующей схемы: