С термином «задача» люди постоянно сталкиваются в повседневной жизни как на бытовом, так и на профессиональном уровне. Каждому из нас приходится решать те или иные проблемы, которые зачастую мы называем задачами. Это могут быть общегосударственные задачи (освоение космоса, воспитание подрастающего поколения, оборона страны и т.п.), задачи определенных коллективов и групп (сооружение объектов, выпуск литературы, установление связей и зависимостей и др.), а также задачи, которые стоят перед отдельными личностями. Проблема решения и чисто математических задач, и задач, возникающих перед человеком в процессе его производственной или бытовой деятельности, изучается издавна, однако до настоящего времени нет общепринятой трактовки самого понятия «задача». В широком смысле слова под задачей понимается некоторая ситуация, требующая исследования и разрешения человеком (или решающей системой).

Отдельно стоят математические задачи, решение которых достигается специальными математическими средствами и методами. Среди них выделяют задачи научные (например, теорема Ферма, проблема Гольбаха и др.), решение которых способствует развитию математики и ее приложений, и задачи учебные, которые служат для формирования необходимых математических знаний, умений и навыков у разных групп обучаемых (школьников, слушателей курсов, студентов и др.) и направлены на изменение качеств личности обучаемого (не знал – знаю, не умел – умею и т.п.).

Учебные математические задачи различаются по характеру их объектов. В одних задачах все объекты математические (числа, геометрические фигуры, функции и т.п.), в других объектами являются реальные предметы (люди, животные, автотранспортные и механические средства, сплавы, жидкости и т.д.) или их свойства и характеристики (количество, возраст, скорость, производительность, длина, масса и т.п.). Задачи, все объекты которых математические (доказательства теорем, вычислительные упражнения, установление признаков изучаемого математического понятия и т.д.), часто называют математическими заданиями.

Математические задачи, в которых есть хотя бы один объект, являющийся реальным предметом, принято называть текстовыми (сюжетными, практическими, арифметическими и т.д.). Перечисленные названия берут начало от способа записи (задача представлена в виде текста), сюжета (описываются реальные объекты, явления, события), характера математических выкладок (устанавливаются количественные отношения между значениями некоторых величин, связанные чаще всего с вычислениями). В последнее время наиболее распространенным является термин «текстовая задача».

Текстовой задачей будем называть описание некоторой ситуации (явления, процесса) на естественном и (или) математическом языке с требованием либо дать количественную характеристику какого-то компонента этой ситуации (определить числовое значение некоторой величины по известным числовым значениям других величин и зависимостям между ними), либо установить наличие или отсутствие некоторого отношения между ее компонентами или определить вид этого отношения, либо найти последовательность требуемых действий.

Придерживаясь современной терминологии, можно сказать, что текстовая задача представляет собой словесную модель ситуации, явления, события, процесса и т.п. Как в любой модели, в текстовой задаче описывается не все событие или явление, а лишь его количественные и функциональные характеристики.

Основная особенность текстовых задач состоит в том, что в них не указывается прямо, какое именно действие (или действия) должно быть выполнено для получения ответа на требование задачи.

В каждой задаче можно выделить:

а) числовые значения величин, которые называются данными, или известными (их должно быть не меньше двух);

б) некоторую систему функциональных зависимостей в неявной форме, взаимно связывающих искомое с данными и данные между собой (словесный материал, указывающий на характер связей между данными и искомыми);

в) требование или вопрос, на который надо найти ответ.

Числовые значения величин и существующие между ними зависимости, т.е. количественные и качественные характеристики объектов задачи и отношений между ними, называют условием (или условиями) задачи. В задаче обычно не одно, а несколько условий, которые называют элементарными.

Требования могут быть сформулированы как в вопросительной, так и в повествовательной форме, их также может быть несколько. Величину, значения которой требуется найти, называют искомой величиной, а числовые значения искомых величин – искомыми, или неизвестными.

Систему взаимосвязанных условий и требований называют высказывательной моделью задачи. Для того чтобы уяснить структуру задачи, надо выявить ее условия и требования, т.е. построить высказывательную модель задачи [10,19,20].

1. Из пункта А одновременно стартуют три бегуна и одновременно финишируют в том же пункте, пробежав по маршруту, состоящему из прямолинейных отрезков АВ, ВС, СА, образующих треугольник АВС. На каждом из указанных отрезков скорости у бегунов постоянны и равны: у первого – 10 км / ч, 16 км / ч и 14 км / ч соответственно; у второго – 12 км / ч, 10 км / ч и 16 км / ч соответственно. Третий бегун в пунктах В и С оказывается не один и меняет скорость на маршруте один раз. Установить, является ли треугольник АВС остроугольным или тупоугольным.

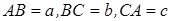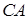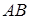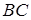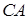Решение . Обозначим стороны треугольника: . Из условия следует, что первый и последний участки -  и  - третий бегун пробегает вместе с первым либо со вторым; причем, если маршрут  он бежит вместе с первым, то маршрут  - вместе с первым, и наоборот. А поскольку он меняет скорость один раз, то его скорости на участках ,  и  соответственно могут быть равными:

1) 10, 10, 16; 3) 12, 12, 14;

2) 10, 16, 16; 4) 12, 14, 14;

Первый вариант отпадает сразу, так как в этом случае третий бегун отстанет от второго.

По аналогичной причине отпадает второй вариант (третий бегун обгонит первого). Остаются два варианта. Соответственно имеем две системы (уравнения составляются на основании условия равенства времени, затрачиваемого на маршрут бегунам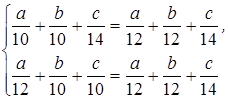и):

 и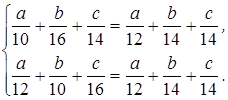

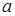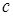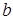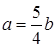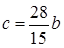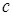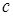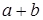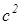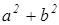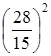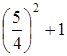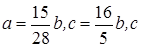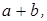
Для каждой системы легко выразить  и  через . Для первой системы , ,  - наибольшая сторона; причем <  и > , так как > . Треугольник тупоугольный. Для второй системы > т.е. этот случай невозможен.

Ответ. Треугольник тупоугольный (тупым является угол АСВ).

2. Вася и Петя победили между собой 39 орехов. Число орехов, доставшихся любому из них, меньше удвоенного числа орехов, доставшихся другому. Квадрат трети числа орехов, доставшихся Пете, меньше числа орехов, доставшихся Васе. Сколько орехов у каждого?

Решение. Если мы обозначим через x и y количество орехов, доставшихся соответственно Васе и Пете, то без труда составим систему из одного уравнения и трех неравенств:

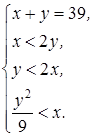
Сложность задачи в третьей части – в решении системы. При этом мы должны помнить, что x и y – целые положительные числа. Из уравнения найдем 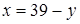. Для y будем иметь систему из трех неравенств:

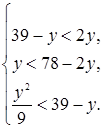
Из первых двух неравенств найдем 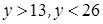. Последнее неравенство перепишем в виде  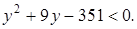Можно, конечно, решить это неравенство. Но лучше поступить иначе. Поскольку y – целое положительное число, то при  будем иметь 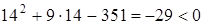, а при  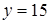будет 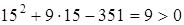, то 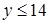. Таким образом, .

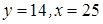Ответ. 25 и 14 орехов.

3. Пункт А находится на берегу реки, ширина которой 400 м, скорость течения 3 км / ч. Пункт В расположен ниже по течению в 4 км от А (если В₁ – проекция В на берег, на котором расположен А, то АВ₁=4 км), на расстоянии 2 км 680 м от противоположного берега (А и В – по разные стороны реки). Турист выехал из А на лодке, пересек реку, оставил на берегу лодку, дошел до В и вернулся тем же путем. На всех участках, по реке и по суше, он двигался прямолинейно. Скорость лодки в стоячей воде 5 км / ч, скорость передвижения туриста пешком 3,2 км / ч. За какое наименьшее время мог проделать свое путешествие турист?

Решение. Пусть турист приплыл в точку С на противоположном берегу. Причем СD = x, где D – пункт, противоположный А (рис. 1,а) ( АD перпендикулярен берегам ). Если время на прохождение участка АС равно t₁, то на участке C D можно найти такую точку С₁, что AC ₁ = 5t ₁ , C ₁ C = 3t ₁ .

Это означает, что вектор 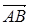 - путь, реально пройденный лодкой, мы представляем в виде суммы двух векторов:  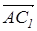- путь, пройденный лодкой,

если бы не было течения, и 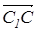 - путь лодки под воздействием одного течения.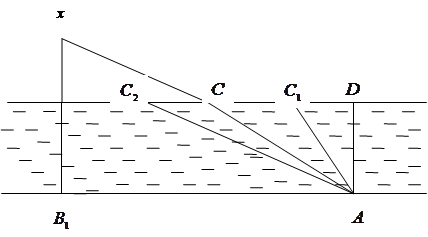

Рис. 1 а)

Записав для треугольника AC₁ D теорему Пифагора, получим

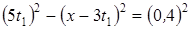
или

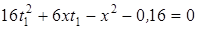. (1)

Аналогично, если t₂ – время на пути от C до A, определив точку С₂ ниже С так, что 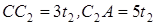, получим для t₂ уравнение

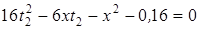. (2)

Поскольку t₁ и t₂ – положительные корни соответственно уравнений (1) и (2), то

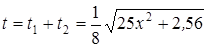
есть время передвижения на лодке. Время движения по суше равно

.

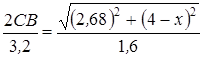Таким образом, время, затраченное на путешествие, будет:

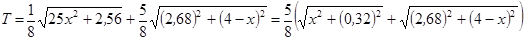
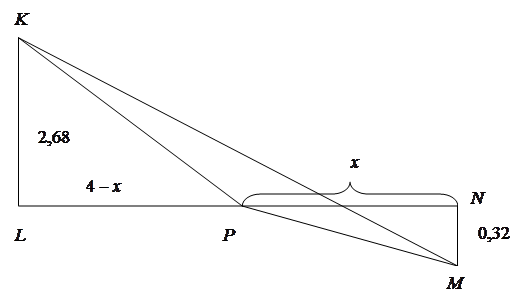
Рис. 1 б)

Рассмотрим два прямоугольных треугольника PNM и KLP: катеты одного x и 0,32, другого 4-x и 2,68, расположенных, как показано на рисунке 1,б. Тогда

.

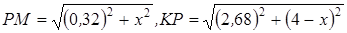Длина ломанной KPM будет минимальной, если точка P лежит на отрезке

KM . Но .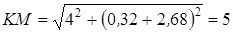

Таким образом, минимальное время будет:

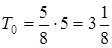 (ч).

Ответ. Наименьшее время, за которое турист мог проделать свое путешествие 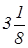 часа [21].