Производственная функция – функция, отображающая зависимость между максимальным объемом производства и количеством используемых факторов производства.
Q = f ( F 1 ; F 2 ;…; Fn )
Где Q – максимальный объем производства при заданных затратах
F1 – количество использованного фактора f1
F2 – количество использованного фактора f2
Fn – количество использованного фактора fn
А если весь набор факторов производства и ресурсов представить как затраты труда, материалов и капитала, производственная функция будет описана следующим образом:
Q = f ( L , M , K )
Где Q – максимальный объем продукции, производимой при данной технологии и определенных факторах производства: L – труд, M – материалы, К – капитал.
Для различных видов производства производственные функции различны, тем не менее, все они имеют общие свойства:
1. Существует предел для роста объема выпуска, который может быть достигнут ростом затрат одного ресурса при прочих равных условиях. Так, в фирме при фиксированном количестве машин и производственных помещений имеется предел роста выпуска путем увеличения дополнительных рабочих, поскольку рабочий не будет обеспечен машинами для работы
2. Существует определенная взаимодополняемость (комплементарность) факторов производства, однако без уменьшения объема выпуска вероятная и определенная взаимозаменяемость данных факторов производства. Так для выпуска блага могут быть использованы различные комбинации ресурсов, можно произвести это благо при использовании меньшего объема капитала и большего объема затрат труда, и наоборот.
Как правило, в большинстве случаев факторы производства являются одновременно и дополнителями и до определенной степени заменителями друг друга. Для таких случаев подходит формула:
Q = Kα Lβ
Данный вид зависимости был проанализирован американскими учеными Коббом и Дугласом и по их имени была названа производственная функция вида:
Y = A Kα Lβ
Где А – коэффициент пропорциональности (линейный коэффициент)
α + β = 1
α : β = 1:3 – пропорции, в которых труд и капитал участвуют в процессе производства (для с/х)
Модификацией (графическим изображением) производственной функции является изокванта.
Изокванта – геометрическое место точек, соответствующих различным сочетаниям производственных факторов, использование которых обеспечивает одинаковый (максимальный) объем выпуска (производства) продукции.
Изкованты могут иметь разную форму соответственно видам производственных функций.
1. Для случаев ресурсов совершенных заменителей карта изоквант (это набор кривых безразличий производства, каждая из которых показывает максимальный выпуск продукции, достигаемые при использовании определенных сочетаний вводимых факторов) представит собой совокупность параллельных прямых с отрицательным наклоном.
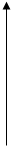 К
К
 |
 L
L
Производственная функция (линейная) имеет вид f ( K , L ) = K + L или Q = aK + bL , где а и b – коэффициенты, отношение которых друг к другу показывает пропорцию замещения одним фактором другого.
2. Для факторов производства, являющихся абсолютными дополнителями и не способными замещать друг друга, изокванты имеют форму английской буквы L.

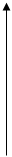 К
К
 L
L
Производственная функция (функция Леонтьева) имеет вид f ( K , L ) = min { K , L } или
Q = min { aK , bL } , где а>0 и b >0 и характеризуют пропорцию дополнения.
Единственно возможным рациональным решением для производителя будет нахождение в точке излома кривой, поскольку движение по вертикальному или горизонтальному ее отрезка означает бессмысленное приращение одного из ресурсов без увеличения объема производства. Чтобы увеличить выпуск продукции, фирме требуется перейти в точку излома вышележащей изокванты.
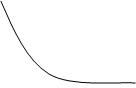
3. Производственная функция Кобба-Дугласа является как бы промежуточным вариантом между линейной и леонтьевской функциями. Два фактора производства являются одновременно и заменителями и дополнителями друг друга. Такая форма изоквант называется стандартной.
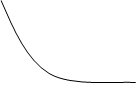
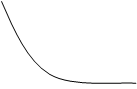
 K
K
 |
Q1
Q2
 Q3 L
Q3 L
Q1, Q2, Q3 – изокванты
Одним из графических инструментов анализа издержек производства (затрат факторов производства) является изокоста.
Изокоста – геометрическое место точек, соответствующее всем комбинациям двух ресурсов, которые можно купить за одинаковую общую сумму денег (т.е. ресурсы, обладающие одинаковой стоимостью).
Изокоста аналогична бюджетной линии потребителя. Наклон ее постоянен вдоль всей прямой и равен ценовому отношению обоих ресурсов (РL/PK)/
 К
К
 L
L
Ряд параллельных изокост характеризует разные уровни совокупных издержек при неизменных ценах факторов или при изменении цен в одинаковой пропорции. Если наклон изокосты меняется, это говорит о том, что при прочих равных условиях, изменяется цена одного из факторов (или же изменяется цена обоих факторов, но в разных пропорциях)
Придерживаясь рационального принципа поведения, производитель стремится минимизировать издержки производства заданного объема продукции. Графическое решение этой задачи предполагает использование нескольких изокост и изокванты, соответствующей заданному объему производства. Для стандартной изокванты (производственной функции Кобба-Дугласа) решение будет следующим:
 К
К
 |

 A
A
 L
L
Изокосты, лежащие ниже изокванты и не имеющие с ней общих точек, означают, что заданный объем производства недостижим при столь низких уровнях издержек.
Изокосты, пересекающие изокванты и имеющие с ней 2 общие точки, означают, что уровень издержке завышен. Всегда можно подобрать иную комбинацию ресурсов, которая обеспечит заданный выпуск продукции при меньших затратах.
Изокоста, проходящая по касательной к изокванте, характеризует тот минимальный уровень издержек, который требуется для выпуска заданного количество продукции. Точка касания заданной изокванты с возможно более низкой изокостой показывает ту комбинацию ресурсов, которую необходимо применять в данном случае. В точке касания углы наклона кривых равны, т.е. МРL/MPK = PL/PK. Графическим путем получена та же формула минимизации издержке, что и алгебраически.
Дата: 2019-12-22, просмотров: 529.